Open Up Resources Logo

Lección 2Temperaturas cambiantes

Sumemos números con signo.

Metas de aprendizaje:

  • Puedo utilizar una recta numérica para sumar números positivos y negativos.

2.1 ¿Cuál es diferente?: flechas

¿Qué pareja de flechas es diferente?

2.2 Más caliente y más frío

  1. Completa la tabla y dibuja un diagrama de recta numérica para cada situación.

    inicio ( ^\circ\text{C} ) cambio ( ^\circ\text{C} )  final ( ^\circ \text{C} ) ecuación de suma
    a +40 10 grados más caliente +50 40 + 10 = 50
    b +40 5 grados más frío
    c +40 30 grados más frío
    d +40 40 grados más frío
    e +40 50 grados más frío

  2. Completa la tabla y dibuja una diagrama de recta numérica para cada situación.

    inicio ( ^\circ\text{C} ) cambio ( ^\circ\text{C} ) final ( ^\circ\text{C} ) ecuación de suma
    a -20 30 grados más caliente
    b -20 35 grados más caliente
    c -20 15 grados más caliente
    d -20 15 grados más frío

¿Estás listo para más?

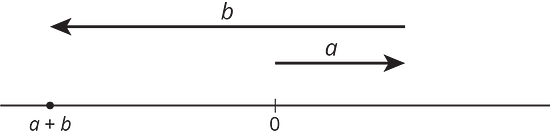
Para los números a y b representados en la figura, ¿qué expresión es igual a |a+b| ?

|a|+|b|

|a|-|b|

|b|-|a|

2.3 Temperaturas de invierno

  1. Un día de invierno, la temperatura en Houston es 8^\circ Celsius. Encuentra las temperaturas en estas otras ciudades. Explica o muestra tu razonamiento.
    1. En Orlando, la temperatura es 10^\circ más caliente que en Houston.
    2. En Salt Lake City, la temperatura es 8^\circ más fría que en Houston.
    3. En Mineápolis, la temperatura es 20^\circ más fría que en Houston.
  2. En Fairbanks, la temperatura es 10^\circ más fría que en Mineápolis. ¿Cuál es la temperatura en Fairbanks?
  3. Usa el applet de termómetro para verificar tus respuestas y explorar tus propios escenarios.
abrir en modo presentación

Resumen de la lección 2

Si la temperatura afuera es  42^\circ y esta aumenta en  7^\circ , entonces podemos sumar la temperatura inicial y el cambio en la temperatura para encontrar la temperatura final.

42 + 7 = 49

Si la temperatura disminuye en 7^\circ , podemos restar 42-7 para encontrar la temperatura final, o podemos pensar en el cambio como \text-7^\circ . Nuevamente, podemos sumar para encontrar la temperatura final.

42 + (\text-7) = 35

En general, podemos representar un cambio en la temperatura con un número positivo si esta aumenta y con un número negativo si disminuye. Luego podemos encontrar la temperatura final al sumar la temperatura inicial y el cambio. Si la temperatura es  3^\circ y la temperatura disminuye en 7^\circ , entonces podemos sumar para encontrar la temperatura final.

3+ (\text-7) = \text-4

Podemos representar números con signo mediante flechas en la recta numérica. Podemos representar números positivos con flechas que comienzan en cero y apuntan a la derecha. Por ejemplo, esta flecha representa +10 porque tiene 10 unidades de longitud y apunta hacia la derecha.

A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the left, and ends at negative 4.There is a solid dot indicated at 4.

Podemos representar números negativos con flechas que comienzan en 0 y apuntan a la izquierda. Por ejemplo, esta flecha representa -4 porque tiene 4 unidades de longitud y apunta hacia la izquierda.

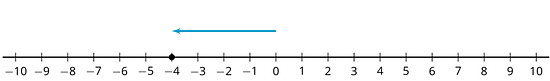
A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the left, and ends at negative 4.There is a solid dot indicated at 4.

Para representar suma, colocamos las flechas "punta con cola". Así, este diagrama representa  3+5 :

A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the right, and ends at 3. A second arrow starts at 3, points to the right, and ends at 8. there is a solid dot indicated at 8.

Y este representa 3 + (\text-5) :

A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the right, and ends at three. A second arrow starts at 3, points to the left, and ends at negative 2. There is a solid dot indicated at negative

Problemas de práctica de la lección 2

    1. La temperatura es -2 ^\circ \text{C} . Si la temperatura aumenta en 15 ^\circ \text{C} , ¿cuál es la nueva temperatura?
    2. A la medianoche la temperatura es -6 ^\circ \text{C} . Al mediodía la temperatura es 9 ^\circ \text{C} . ¿En cuánto aumentó la temperatura?

  2. Completa cada desigualdad con un número que la haga verdadera.

    1. _____ < 7^\circ \text{C}
    2. _____ < \text- 3^\circ \text{C}
    3. \text- 0.8^\circ \text{C} < _____ < \text- 0.1^\circ \text{C}
    4. _____ > \text- 2^\circ \text{C}

  3. Dibuja un diagrama para representar cada una de estas situaciones. Luego escribe una expresión de suma que represente la temperatura final.

    1. La temperatura era  80 ^\circ \text{F} y bajó 20 ^\circ \text{F} .
    2. La temperatura era \text-13 ^\circ \text{F} y subió 9 ^\circ \text{F} .
    3. La temperatura era \text-5 ^\circ \text{F} y bajó 8 ^\circ \text{F} .

  4. Decide si cada una de las tablas podría representar una relación proporcional. Si la relación puede ser proporcional, ¿cuál sería la constante de proporcionalidad?

    1. El número de ruedas en un grupo de buses. 

      número de buses número de ruedas ruedas por cada bus
      5 30
      8 48
      10 60
      15 90

    2. El número de ruedas de un tren.

      número de vagones número de ruedas ruedas por cada vagón
      20 184
      30 264
      40 344
      50 424

  5. Noah fue designado para hacer 64 galletas para la feria de pastelería. Él hizo 125% de esta cantidad. El 90% de las galletas que hizo se vendieron. ¿Cuántas galletas de Noah quedaron después de la venta de pastelería?