Lección 11Hagamos cortes a sólidos
Veamos qué formas se obtienen cuando se hacen cortes a un objeto tridimensional.
Metas de aprendizaje:
- Puedo explicar que cuando se hacen cortes a una figura de tres dimensiones, se crea una cara que es de dos dimensiones.
- Puedo imaginar distintas secciones transversales de prismas y pirámides.
11.1 Prismas, pirámides y poliedros
Describe cada objeto de la forma más precisa posible. Haz clic en el applet y arrastra el ratón para mostrar cómo gira el objeto en 3D.
11.2 ¿Cuál es la sección transversal?
Estos son un prisma rectangular y una pirámide que tienen base y altura iguales. Arrastra el punto rojo grande hacia arriba y abajo para mover el plano a través de los sólidos.
-
Si cortamos cada sólido paralelo a su base y hacia la mitad, ¿qué formas de secciones transversales obtendremos? ¿En qué se parecen las secciones transversales? ¿En qué se diferencian?
-
Si cortamos cada sólido paralelo a su base y cerca a su parte superior, ¿qué formas de secciones transversales obtendremos? ¿En qué se parecen las secciones transversales? ¿En qué se diferencian?
¿Estás listo para más?
Describe las secciones transversales que resultarían de hacer cortes perpendiculares a la base de cada sólido.
11.3 Clasificación de tarjetas: secciones transversales
11.4 Dibujemos secciones transversales
Usa el applet para dibujar cada sección transversal y descríbela en palabras.
-
Este es un applet con un prisma rectangular de 4 unidades por 2 unidades por 3 unidades.
- Un plano corta el prisma, paralelo a las caras inferior y superior.
- El plano se mueve hacia arriba y corta el prisma a una altura distinta.
- Un plano vertical corta el prisma diagonalmente.
- Una pirámide de base cuadrada tiene una base de 4 unidades por 4 unidades. Su altura también es de 4 unidades.
- Un plano corta la pirámide paralelo a la base.
- Un plano vertical corta la pirámide.
- Un cubo tiene una arista de longitud 4.
- Un plano corta la esquina del cubo.
- El plano se aleja de la esquina y hace un corte a través de la mitad del cubo.
Resumen de la lección 11
Cuando hacemos cortes a un objeto de tres dimensiones, exponemos nuevas caras que son de dos dimensiones. La cara bidimensional es una sección transversal. Hay varios tipos de secciones transversales posibles al hacer cortes al mismo objeto tridimensional.
Estos son dos pimientos. A uno se le hacen cortes horizontales y al otro se le hacen cortes verticales que producen secciones transversales diferentes.

Las huellas de las rebanadas representan las caras bidimensionales creadas por cada corte.
Toma práctica imaginar cuál será la sección transversal de un objeto de tres dimensiones para diferentes cortes. ¡Ayuda experimentar y ver uno mismo lo que ocurre!
Términos del glosario
Una sección transversal es la nueva cara que ves cuando le haces un corte a una figura tridimensional.
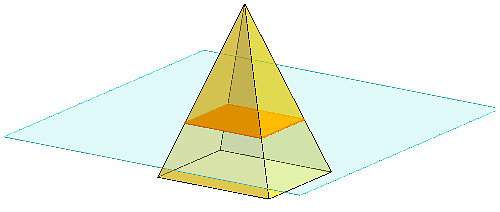
Por ejemplo, si tomas una pirámide rectangular y le haces un corte paralelo a la base, la sección transversal que obtienes es un rectángulo más pequeño.
Problemas de práctica de la lección 11
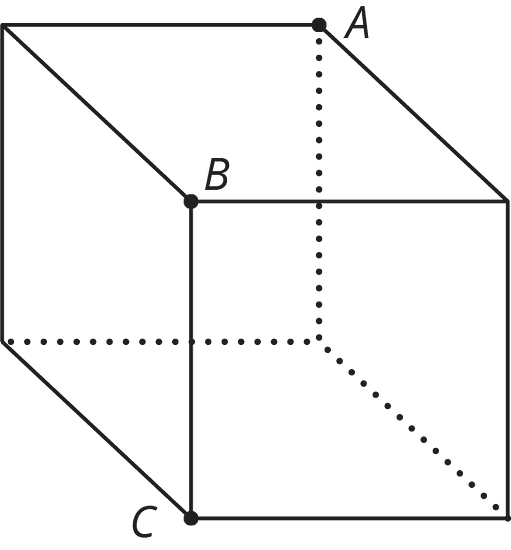
Un cubo se corta en dos partes al hacer un solo corte que pasa a través de los puntos , y . ¿Cuál es la forma de la sección transversal?
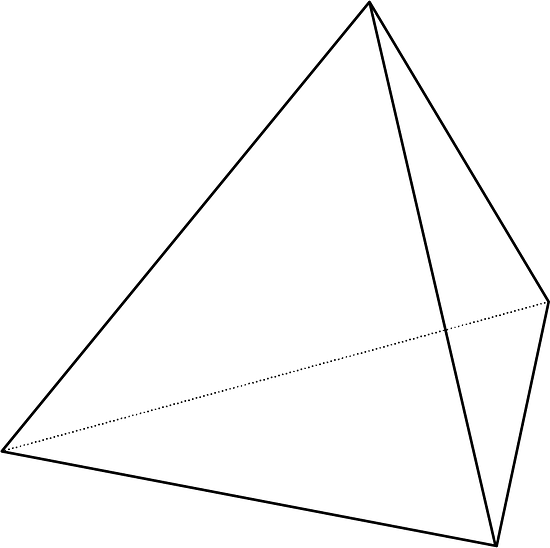
Describe cómo hacer cortes a la figura tridimensional para que resulten las secciones transversales que se muestran.
Figura de tres dimensiones:
Secciones transversales:

Estas son dos figuras tridimensionales.
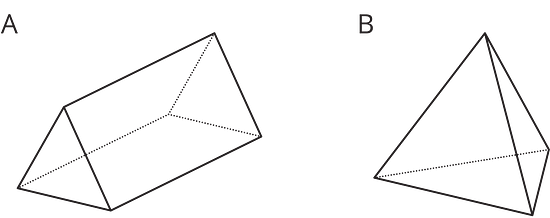 Describe una manera de hacer cortes a una de las figuras para que la sección transversal sea un rectángulo.
Describe una manera de hacer cortes a una de las figuras para que la sección transversal sea un rectángulo.Cada fila tiene la medida en grados de dos ángulos suplementarios. Completa la tabla.
medida de un ángulo medida de su suplemento Hace dos meses, el precio en dólares de un teléfono celular era .
- El mes pasado, el precio del teléfono aumentó un 10%. Escribe una expresión para el precio del teléfono el mes pasado.
- Este mes, el precio del teléfono disminuyó un 10%. Escribe una expresión para el precio del teléfono este mes.
- ¿El precio del teléfono este mes es el mismo que hace dos meses? Explica tu razonamiento.