Lección 14Área de superficie de prismas rectos
Estudiemos el área de superficie de prismas.
Metas de aprendizaje:
- Puedo encontrar y utilizar atajos al calcular el área de superficie de un prisma.
- Puedo representar el desarrollo plano de un prisma como ayuda para calcular su área de superficie.
14.1 Multifacético
Tu profesor les mostrará un prisma.
- ¿Cuáles son algunas cosas del objeto que podrían medir?
-
¿Qué unidades usarían para estas mediciones?
14.2 Demasiadas caras
Esta es una imagen del prisma de tu profesor:

Tres estudiantes intentan calcular el área de superficie de este prisma.
- Noah dice: "Esto es mucho trabajo. Tenemos que calcular el área de 14 caras diferentes y sumarlas".
- Elena dice: "No es tan difícil. Todos los 12 rectángulos son copias idénticas, así que podemos calcular el área de uno de ellos, multiplicarla por 12 y luego sumarle las áreas de las 2 bases".
- Andre dice: "Esperen, ¡veo otra manera! Imaginen que se desdobla el prisma en un desarrollo plano. Podemos usar 1 rectángulo grande en lugar de 12 pequeños".
- ¿Estás de acuerdo con alguno de ellos? Explica tu razonamiento.
- ¿Qué tan grande es "el rectángulo grande" del que habla Andre? Explica o muestra tu razonamiento. Si tienes dificultades, considera dibujar un desarrollo plano para el prisma.
- ¿El método de Noah siempre funcionará para determinar el área de superficie de cualquier prisma?, ¿el método de Elena?, ¿el método de Andre? Prepárate para explicar tu razonamiento.
-
¿Cuál método prefieres? ¿Por qué?
14.3 Retomemos un prisma pentagonal
-
Entre tú y tu compañero, elijan quién usará cada uno de estos dos métodos para determinar el área de superficie del prisma:
- Sumar las áreas de todas las caras.
- Usar el perímetro de la base.
- Usa el método que escogiste para calcular el área de superficie del prisma. Muestra tu razonamiento. Organízalo de manera que otros puedan entenderlo.
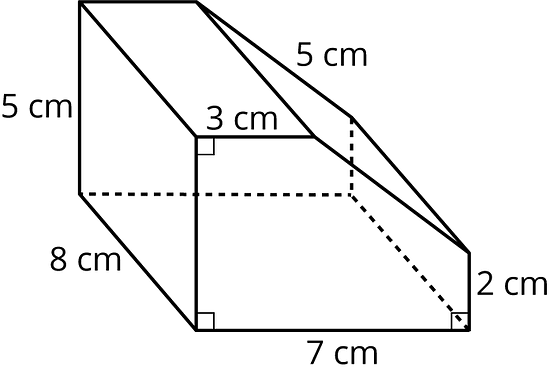
- Intercambia papeles con tu compañero y verifica su trabajo. Discutan sus razonamientos. Si están en desacuerdo, trabajen para llegar a un acuerdo.
¿Estás listo para más?


En una baraja de cartas, cada carta mide 6 cm por 9 cm.
-
Cuando está apilada, la baraja tiene 2 cm de alta, como se muestra el la primera foto. Encuentra el volumen de esta baraja de cartas.
-
Luego, la pila de cartas se despliega en abanico, como se muestra en la segunda imagen. Ahora la distancia del punto extremo a la derecha en la carta inferior al punto extremo a la derecha en la carta superior es de 7 cm en lugar de 2 cm. Determina el volumen de la nueva pila.
Resumen de la lección 14
Para hallar el área de superficie de una figura tridimensional cuyas caras están compuestas por polígonos, podemos hallar el área de cada cara ¡y sumarlas!
Algunas veces hay maneras de simplificar nuestro trabajo. Por ejemplo, todas las caras de un cubo con lado de longitud son iguales. Podemos hallar el área de una cara y multiplicarla por 6. Como el área de una cara de un cubo es , el área de superficie de un cubo es .
Podemos usar esta técnica para hacer más rápido el cálculo del área de superficie de cualquier figura que tenga caras que son iguales.
Para los prismas, hay otra manera. Podemos tratar el prisma como si tuviera tres partes: dos bases idénticas y un rectángulo grande que se ha pegado a lo largo de los bordes de las bases. El rectángulo tiene la misma altura que el prisma y su ancho es el perímetro de la base. Para hallar el área de superficie, sumamos el área de este rectángulo al área de las dos bases.
Problemas de práctica de la lección 14
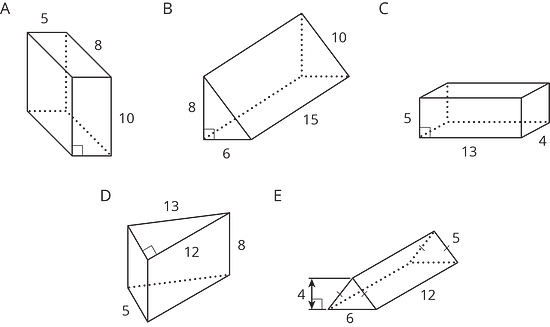
Las longitudes de las aristas se dan en unidades. Encuentra el área de superficie de cada prisma en unidades cuadradas.
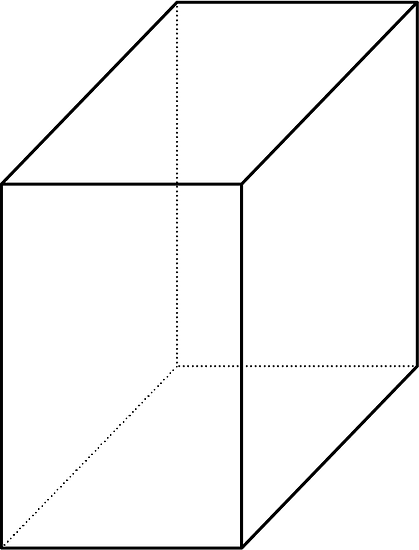
Priya dice, "Sin importar de qué manera se hagan cortes a este prisma rectangular, la sección transversal será un rectángulo". Mai dice, "No estoy segura". Describe un corte en el que Mai puede estar pensando.
es la intersección de la recta y la recta . Encuentra la medida de cada uno de los ángulos.
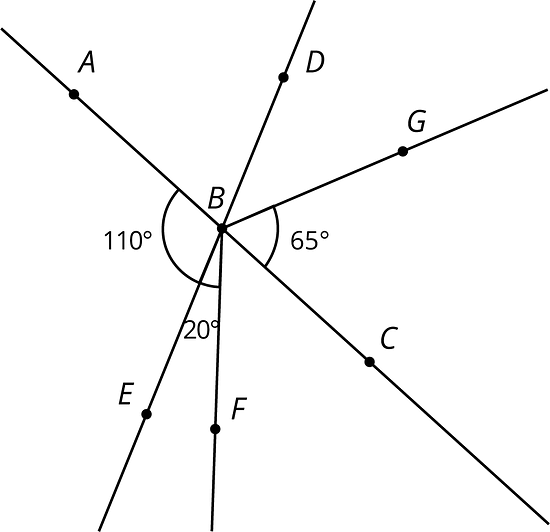
-
La medida del ángulo
-
La medida del ángulo
-
La medida del ángulo
-
La medida del ángulo
-
La medida del ángulo
-
Escribe cada expresión usando menos términos.
- Encuentra el 44% de 625 utilizando el hecho de que el 40% de 625 es 250 y el 4% de 625 es 25.
- ¿Cuánto es 4.4% de 625?
- ¿Cuánto es 0.44% de 625?