Lección 15Estimar medidas de centro de la población
Usemos muestras para estimar medidas de centro de la población.
Metas de aprendizaje:
- Puedo evaluar la variabilidad de una muestra para obtener una idea de qué tan acertada es mi estimación.
- Puedo hacer una estimación de la media y la mediana de una población basado en una muestra de la población.
15.1 Describir el centro
¿Usarían la mediana o la media para describir el centro de cada conjunto de datos? Expliquen su razonamiento.
Estaturas de 50 jugadores de baloncesto
Edades de 30 personas en una cena familiar
Pesos de las mochilas de estudiantes de sexto grado
Cantidad de libros que lee un estudiante en las vacaciones de verano
15.2 Tres programas de televisión diferentes
Estas son las edades (en años) de una muestra aleatoria de 10 espectadores de 3 programas de televisión diferentes. Los programas se llaman, "Experimentos científicos que TÚ puedes hacer", "Aprendamos a leer" y "Concurso de preguntas".
| muestra 1 | 6 | 6 | 5 | 4 | 8 | 5 | 7 | 8 | 6 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| muestra 2 | 15 | 14 | 12 | 13 | 12 | 10 | 12 | 11 | 10 | 8 |
| muestra 3 | 43 | 60 | 50 | 36 | 58 | 50 | 73 | 59 | 69 | 51 |
- Calculen la media de una de las muestras. Asegúrense de que cada persona de su grupo trabaje con una muestra diferente. Anoten las respuestas de todas las tres muestras.
- ¿Cuál muestra creen que representa cada programa? Expliquen su razonamiento.
15.3 ¿Quién ve qué?
Estas son tres muestras adicionales de las edades de los espectadores recolectadas de estos mismos 3 programas de televisión.
| muestra 4 | 57 | 71 | 5 | 54 | 52 | 13 | 59 | 65 | 10 | 71 |
|---|---|---|---|---|---|---|---|---|---|---|
| muestra 5 | 15 | 5 | 4 | 5 | 4 | 3 | 25 | 2 | 8 | 3 |
| muestra 6 | 6 | 11 | 9 | 56 | 1 | 3 | 11 | 10 | 11 | 2 |
- Calculen la media de una de estas muestras. Anoten todas las tres respuestas.
- ¿Qué programa creen que cada una de estas muestras representa? Expliquen su razonamiento.
- Para cada programa, estimen la edad media de todos los espectadores del programa.
-
Calculen la desviación media absoluta de una de las muestras de un programa. Asegúrense de que cada persona de su grupo trabaje con una muestra diferente. Anoten todas las tres respuestas.
Aprendamos a leer
Experimentos científicos que TÚ puedes hacerConcurso de preguntas ¿Muestra número qué? MAD - ¿Qué nos dicen los diferentes valores de la MAD sobre cada grupo?
- Un anunciante tiene un comercial televisivo dirigido a personas entre 15 y 16 años de edad. Con base en estas muestras, ¿alguno de estos programas sería una buena opción para este anuncio televisivo? Expliquen o muestren su razonamiento.
15.4 Críticas de películas
Un sitio web sobre críticas de películas hizo que muchas personas calificaran una película nueva en una escala de 0 a 100. Este es el diagrama de puntos que exhibe una muestra aleatoria de 20 de estas críticas.
- ¿Cuál de las dos, la media o la mediana, sería una mejor medida de centro para estos datos? Expliquen su razonamiento.
- Usen la muestra para estimar la medida de centro que escogieron para todas las críticas.
- Para esta muestra, la desviación media absoluta es 19.6 y el rango intercuartil es 15. ¿Cuál de estos valores corresponde a la medida de centro que escogieron?
- Las películas deben tener una calificación promedio de 75 o más en todas las críticas que recibieron en el sitio web para que sean consideradas para un premio. ¿Creen que esta película será considerada para el premio? Usen la medida de centro y la medida de variabilidad que escogieron para justificar su respuesta.
¿Estás listo para más?
Estimen las temperaturas normales de hoy en los Estados Unidos mirando las temperaturas actuales en varios lugares de todo el país. Usen los datos que recolectaron para decidir la medida de centro adecuada para el país y calculen la medida de variación correspondiente para su muestra.
Resumen de la lección 15
Algunas poblaciones tienen mayor variabilidad que otras. Por ejemplo, esperaríamos mayor variabilidad en los pesos de los perros en un parque para perros que en una convención de beagles.
Parque para perros:
- Peso medio: 12.8 kg
- MAD: 2.3 kg

Convención de beagles:
- Peso medio: 10.1 kg
- MAD: 0.8 kg

La MAD más pequeña indica que hay menor variabilidad en los pesos de los beagles. Esperaríamos que la media de los pesos de una muestra, que es seleccionada aleatoriamente de un grupo de beagles, nos diera una estimación más acertada de la media de los pesos de todos los beagles que una muestra del mismo tamaño de los perros en el parque.
En general, una muestra de tamaño semejante de una población con menos variabilidad tiene más probabilidad de tener una media cercana a la media de la población.
Problemas de práctica de la lección 15
Se seleccionó una muestra aleatoria de 15 artículos.
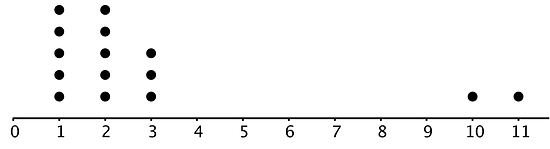
Para este conjunto de datos, ¿cuál es una mejor medida de centro, la media o la mediana? Explica tu razonamiento.
Un desarrollador de videojuegos quiere saber cuánto se demora la gente en completar su nuevo juego. Se encuesta un muestra aleatoria de 13 jugadores, preguntándoles cuánto tardaron en completar su nuevo juego (en minutos).
1,235 952 457 1,486 1,759 1,148 548 1,037 1,864 1,245 976 866 1,431 - Estima la mediana de los tiempos que se gastaron todos los usuarios en completar el juego.
- Encuentra el rango intercuartil (IQR) de esta muestra.
Han y Priya quieren saber la media de las estaturas de los 30 estudiantes en su clase de baile. Cada una selecciona una muestra aleatoria de 5 estudiantes.
- La estatura media en la muestra de Han es 59 pulgadas.
- La estatura media en la muestra de Priya es 61 pulgadas.
¿Te sorprende que las medias de las dos muestras sean distintas? ¿Las medias de las poblaciones son distintas? Explica tu razonamiento.Clare y Priya tomaron, cada una, una muestra aleatoria de 25 estudiantes en su escuela.
- Clare le preguntó a cada estudiante en su muestra cuánto tiempo gastan haciendo tareas cada noche. La media de la muestra fue 1.2 horas y la MAD fue 0.6 horas.
- Priya le preguntó a cada estudiante en su muestra cuánto tiempo gastan viendo televisión cada noche. La media de la muestra fue 2 horas y la MAD fue 1.3 horas.
-
En su escuela, ¿piensas que hay mayor variabilidad en la cantidad de tiempo que los estudiantes gastan haciendo tareas o en el tiempo que gastan viendo televisión? Explica tu razonamiento.
-
Clare estima que los estudiantes en su escuela gastan un promedio de 1.2 horas cada noche haciendo tareas. Priya estima que los estudiantes en su escuela gastan un promedio de 2 horas cada noche viendo televisión. ¿Cuál de estas dos estimaciones es probablemente más cercana al valor real de la media para todos los estudiantes en su escuela? Explica tu razonamiento.