Lección 2Cuadrícula circular
Dilatemos figuras sobre cuadrículas circulares.
Metas de aprendizaje:
- Puedo aplicar dilataciones a figuras sobre una cuadrícula circular cuando el centro de dilatación es el centro de la cuadrícula.
2.1 Observa y pregúntate: círculos concéntricos
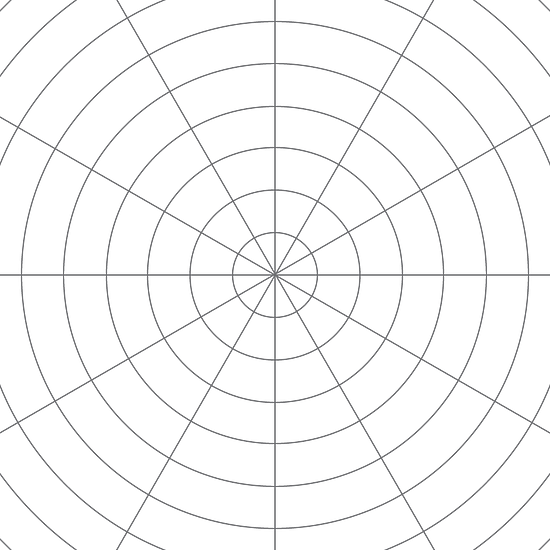
2.2 Una gota en la superficie
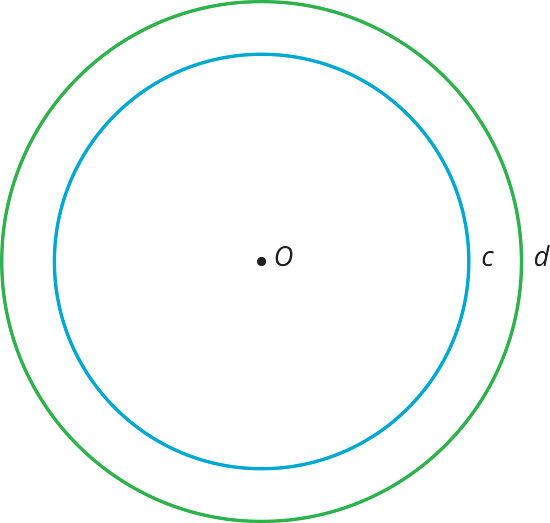
El círculo grande d es una dilatación del círculo pequeño c. es el centro de dilatación.
-
Dibuja cuatro puntos sobre el círculo pequeño usando la herramienta "Punto sobre un objeto".
-
Dibuja los rayos desde a través de cada uno de esos cuatro puntos. Elige la herramienta "Semirrecta", luego el punto y luego el segundo punto.
-
Marca los puntos de intersección de los rayos y el círculo d seleccionando la herramienta "Intersección" y haciendo clic sobre el punto de intersección.
-
Completa la tabla. En la fila etiquetada S, escribe la distancia entre y el punto sobre el círculo pequeño, en unidades de la cuadrícula. En la fila etiquetada L, escribe la distancia entre y el punto correspondiente del círculo más grande, en unidades de la cuadrícula. Mide las distancias entre pares de puntos seleccionando la herramienta Distancia, y luego haciendo clic sobre los dos puntos.

S L - El centro de dilatación es el punto . ¿Cuál es el factor de escala que lleva el círculo más pequeño al círculo más grande? Explica tu razonamiento.
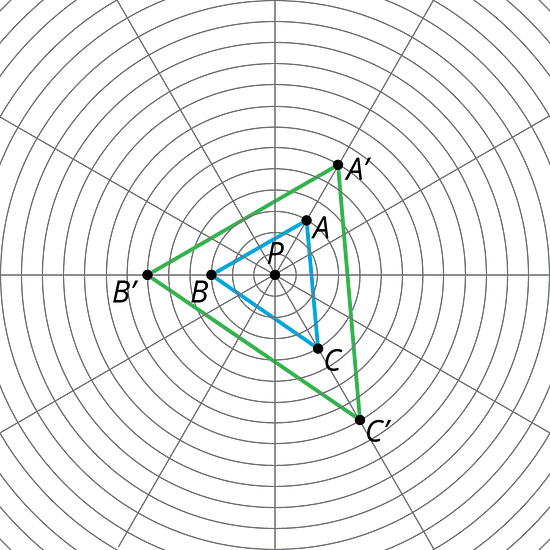
2.3 Cuadrilátero sobre una cuadrícula circular
-
Dilata cada vértice del polígono usando como el centro de dilatación y un factor de escala 2.
- Dibuja segmentos entre los puntos dilatados para crear un nuevo polígono.
-
¿Cuáles son algunas cosas que observas sobre el nuevo polígono?
-
Elige algunos puntos más en los lados del polígono original y transfórmalos usando la misma dilatación. ¿Qué observas?
-
Dilata cada vértice del polígono usando como el centro de dilatación y un factor de escala .
-
¿Qué observas sobre este nuevo polígono?
¿Estás listo para más?
Supongamos que es un punto que no está sobre el segmento de recta . Llamemos a la dilatación del segmento de recta que usa como centro y tiene factor de escala 2. Experimenta con una cuadrícula circular para hacer predicciones acerca de si cada uno de los siguientes enunciados tiene que ser verdadero, puede ser verdadero o tiene que ser falso.
- es el doble de largo que .
- mide 5 unidades más que .
- El punto está sobre .
- y se intersecan.
2.4 Un cuadrilátero y círculos concéntricos
-
Dilata el polígono usando como el centro de dilatación y un factor de escala . La imagen de ya se muestra en el diagrama. (Puede que tengas que dibujar más rayos que salgan de para encontrar las imágenes de otros puntos).
Resumen de la lección 2
Una cuadrícula circular como esta puede ser útil para realizar dilataciones.
El radio del círculo más pequeño mide una unidad y el radio de cada círculo sucesivo mide una unidad más que el anterior.
Como los círculos de la cuadrícula están a la misma distancia, el segmento tiene el doble de la longitud del segmento y lo mismo es cierto para los otros puntos.
Términos del glosario
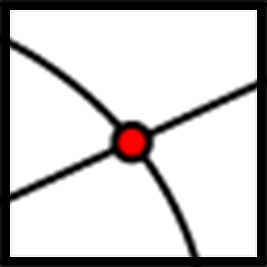
El centro de una dilatación es un punto fijo en un plano. Es el punto desde el cual medimos las distancias en una dilatación.
En este diagrama, el punto es el centro de la dilatación.
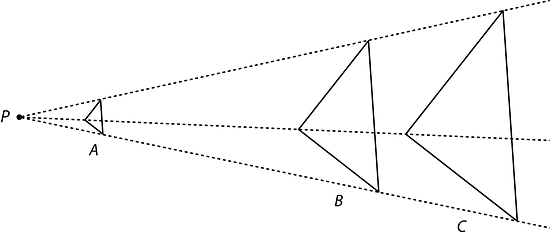
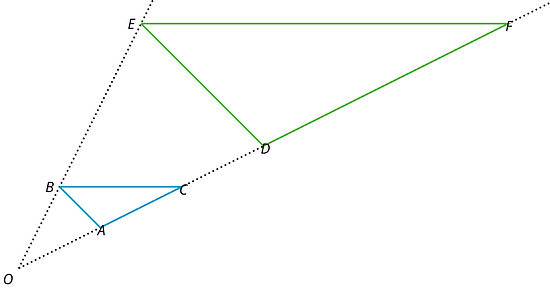
Una dilatación es una transformación en la cual cada punto de una figura cambia su distancia a un punto fijo al moverse sobre la recta que pasa por el punto fijo. El punto fijo es el centro de la dilatación. Todas las distancias originales se multiplican por el mismo factor de escala.
Por ejemplo, el triángulo es una dilatación del triángulo . El centro (el punto fijo) es y el factor de escala es 3.
Esto significa que todos los puntos del triángulo están 3 veces tan lejos de como todos los puntos correspondientes del triángulo .
Problemas de práctica de la lección 2
Estos son los círculos y . El punto es el centro de dilatación, y la dilatación lleva el círculo al círculo .
- Marca un punto en el círculo . Etiqueta el punto . Marca a dónde va cuando se realiza la dilatación.
- Marca un punto en el círculo . Etiqueta el punto . Marca un punto que la dilatación lleve a .
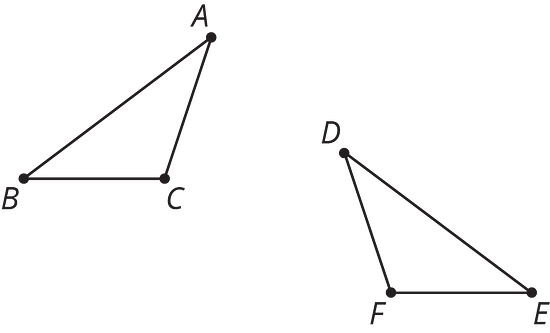
Este es el triángulo .

- Dilata cada vértice del triángulo usando como el centro de dilatación y un factor de escala de 2. Dibuja el triángulo que une los tres puntos nuevos.
- Dilata cada vértice del triángulo usando como el centro de dilatación y un factor de escala de . Dibuja el triángulo que une los tres puntos nuevos.
-
Mide el lado más largo de los tres triángulos. ¿Qué observas?
-
Mide los ángulos de cada triángulo. ¿Qué observas?
Describe una transformación rígida que podrías usar para mostrar que los triángulos son congruentes.
La recta se dividió en tres ángulos.
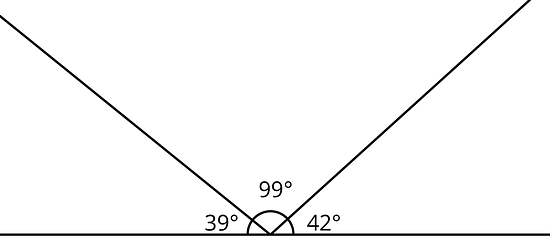
¿Existe un triángulo con estas tres medidas de ángulos? Explica.