Lección 9Cocientes de longitudes de los lados de triángulos semejantes
Encontremos las longitudes de los lados que faltan en triángulos.
Metas de aprendizaje:
- Puedo decidir si dos triángulos son semejantes examinando los cocientes de las longitudes de lados correspondientes.
- Puedo encontrar las longitudes de los lados que faltan en un par de triángulos semejantes usando los cocientes de las longitudes de los lados.
9.1 Dos-tres-cuatro y cuatro-cinco-seis
Las longitudes de los lados del triángulo son 2, 3 y 4. Las longitudes de los lados del triángulo son 4, 5 y 6. ¿El triángulo es semejante al triángulo ?
9.2 Cocientes de lados en triángulos semejantes
El profesor te asignará una de las tres columnas de la segunda tabla.
El triángulo es semejante a los triángulos , y . Los factores de escala de las dilataciones que muestran que el triángulo es semejante a cada triángulo están en la tabla.
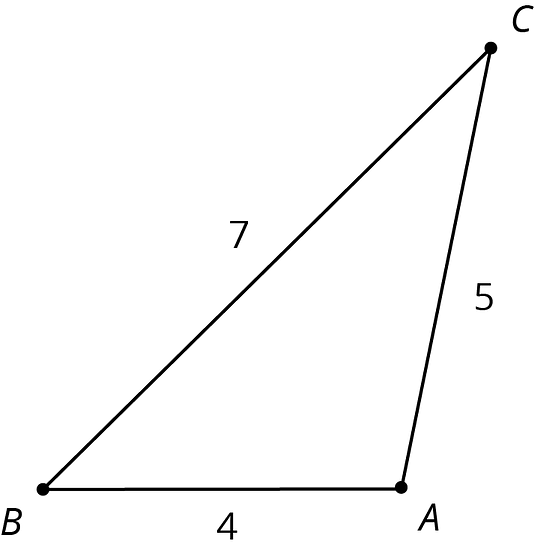
| triángulo | factor de escala | longitud del lado corto | longitud del lado mediano | longitud del lado largo |
|---|---|---|---|---|
| 1 | 4 | 5 | 7 | |
| 2 | ||||
| 3 | ||||
| triángulo | (lado largo) (lado corto) | (lado largo) (lado mediano) | (lado mediano) (lado corto) |
|---|---|---|---|
| o | |||
- Encuentra las longitudes de los lados de los triángulos , y . Escríbelas en la primera tabla.
-
En los cuatro triángulos, encuentra el cociente de las longitudes de los lados que se te asignaron y escríbelos en la segunda tabla. ¿Qué observas en estos cocientes?
- Compara tus resultados con los de tus compañeros y completa la tabla.
¿Estás listo para más?
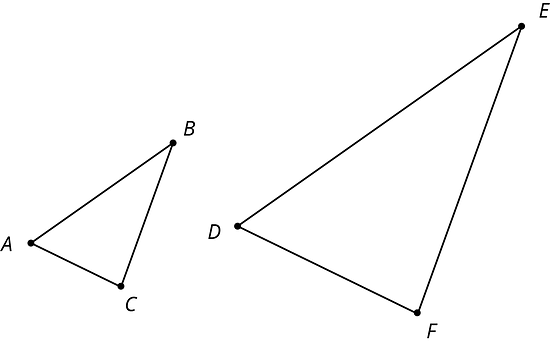
Los triángulos y son semejantes. Explica por qué .
9.3 Usemos los cocientes de los lados para encontrar las longitudes de los lados de triángulos semejantes
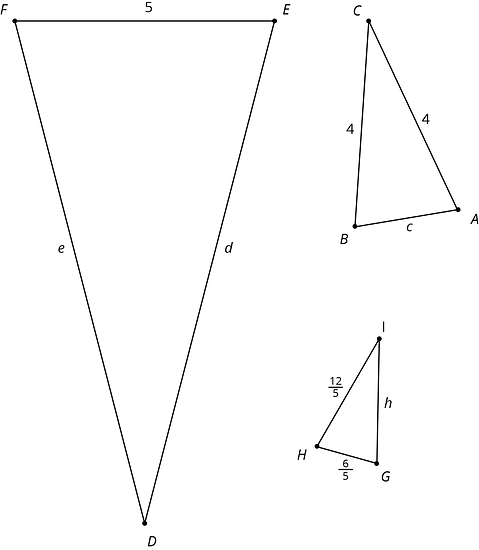
Los triángulos , y son semejantes. Todas las longitudes de los lados de los triángulos tienen las mismas unidades. Encuentra las longitudes de los lados que son desconocidas.
Resumen de la lección 9
Si dos polígonos son semejantes, entonces las longitudes de los lados de un polígono se multiplican por el mismo factor de escala para obtener las longitudes de los lados correspondientes del otro polígono. Para estos triángulos el factor de escala es 2:
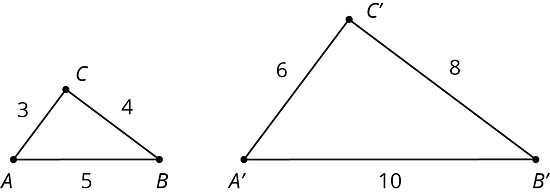
Esta es una tabla que muestra las relaciones entre la longitud de los lados corto y mediano del triángulo pequeño y del grande.
| triángulo pequeño | triángulo grande | |
|---|---|---|
| lado mediano | 4 | 8 |
| lado corto | 3 | 6 |
| (lado mediano) (lado corto) |
Las longitudes del lado mediano y del lado corto tienen una razón de . Esto significa que el lado mediano de cada triángulo es tan largo como el lado corto.
Podemos usar estos hechos para calcular las longitudes que faltan en polígonos semejantes. Por ejemplo, los triángulos y que se muestran aquí son semejantes. Encontremos la longitud del segmento .

En el triángulo , el lado es el doble de largo que el lado , entonces esto debe cumplirse para cualquier triángulo que sea semejante al triángulo . Dado que tiene 1.2 unidades de largo y , la longitud del lado es 2.4 unidades.
Problemas de práctica de la lección 9
Estos dos triángulos son semejantes.
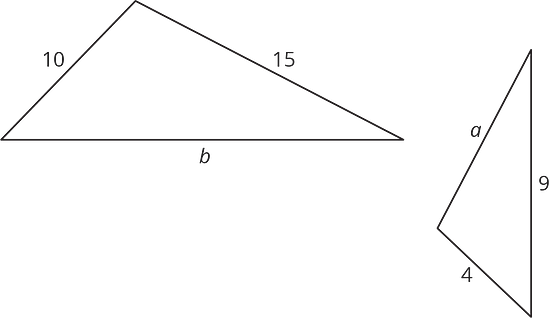
¿Cuánto valen y ? Nota: las dos figuras no están dibujadas a escala.
Este es el triángulo . El triángulo es semejante a con factor de escala .

- Dibuja cómo se vería el triángulo .
-
¿En qué se parecen o diferencian las medidas de los ángulos del triángulo a las del triángulo ? Explica cómo lo sabes.
-
¿Cuáles son las longitudes de los lados del triángulo ?
- Para el triángulo , calcula (lado largo) (lado mediano) y compara el resultado con el del triángulo .
Los dos triángulos que se muestran son semejantes. Encuentra el valor de .

El diagrama muestra dos triángulos anidados que comparten un vértice. Encuentra un centro y un factor de escala para una dilatación que movería el triángulo grande al triángulo pequeño.
