Lección 11Ecuaciones de todo tipo de rectas
Escribamos ecuaciones de rectas verticales y horizontales.
Metas de aprendizaje:
- Puedo escribir ecuaciones de rectas que tienen una pendiente positiva o una pendiente negativa.
- Puedo escribir ecuaciones de rectas verticales y horizontales.
11.1 ¿Cuál es diferente?: pares de rectas
¿Cuál es diferente?
11.2 Siempre iguales
-
Ubica por lo menos 10 puntos cuya coordenada sea -4. ¿Qué observas acerca de ellos?
-
¿Cuál ecuación sirve para representar todos los puntos que tienen coordenada de -4? Explica cómo lo sabes.
-
Ubica por lo menos 10 puntos cuya coordenada sea 3. ¿Qué observas acerca de ellos?
-
¿Cuál ecuación sirve para representar todos los puntos que tienen coordenada de 3? Explica cómo lo sabes.
-
Grafica la ecuación .
-
Grafica la ecuación .
¿Estás listo para más?
- Dibuja el rectángulo con vértices en , , , .
- Para cada uno de los cuatro lados del rectángulo, escribe una ecuación que represente la recta que contiene el lado.
- Un rectángulo tiene lados sobre las gráficas de las rectas , , , . Halla las coordenadas de cada vértice.
11.3 El mismo perímetro
-
Hay muchos rectángulos posibles que tienen un perímetro de 50 unidades. Completa la tabla con el largo, y el ancho, , de por lo menos 10 de esos rectángulos.
-
La gráfica muestra un rectángulo cuyo perímetro es 50 unidades y que tiene su vértice inferior izquierdo en el origen y dos lados sobre los ejes. En la misma gráfica, usando los valores de tu tabla dibuja más rectángulos que tengan perímetro de 50 unidades. Asegúrate de que cada rectángulo tenga un vértice inferior izquierdo en el origen y dos lados sobre los ejes.
-
Todos los rectángulos tienen un vértice que está en el primer cuadrante. Estos vértices están sobre una recta. Dibuja la recta en la misma gráfica y escribe una ecuación para esta.
-
¿Cuál es la pendiente de esta recta? ¿De qué manera la pendiente nos indica cómo cambia el ancho cuando cambia el largo (o viceversa)?
Resumen de la lección 11
En el plano de coordenadas, las rectas horizontales representan situaciones en las que el valor de nunca cambia mientras el valor de está cambiando. Por ejemplo, la recta horizontal que pasa por el punto se puede describir en palabras como "el valor de siempre es 13 para todos los puntos sobre la recta". Una ecuación que dice lo mismo es .
Las rectas verticales representan situaciones en las que el valor de nunca cambia mientras el valor de está cambiando. La ecuación describe a una recta vertical que pasa por el punto .
Problemas de práctica de la lección 11
Supongamos que quieres graficar la ecuación .
- Describe los pasos que seguirías para dibujar la gráfica.
- ¿Cómo comprobarías que la gráfica que dibujaste es correcta?
Dibuja las siguientes rectas y luego escribe una ecuación para cada una.
- La pendiente es 0, la intersección con el eje es 5
- La pendiente es 2, la intersección con el eje es
- La pendiente es , la intersección con el eje es 1
- La pendiente es , la intersección con el eje es

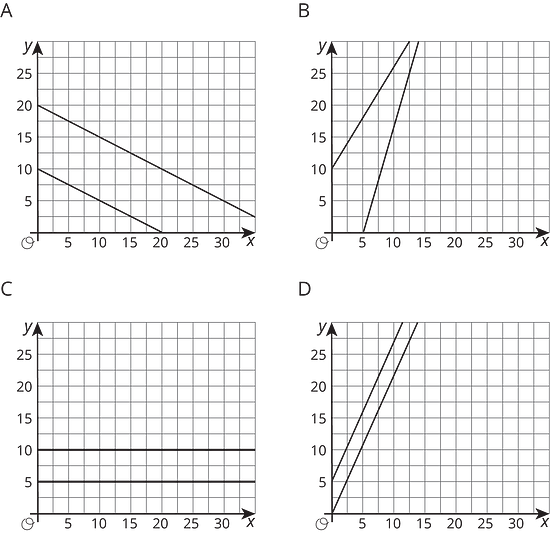
Escribe una ecuación para cada recta.

Un editor quiere averiguar qué tan grueso será su nuevo libro. El libro tiene una portada y una contraportada, cada una tiene un grosor de de pulgada. Él puede elegir el tipo de papel para imprimir el libro.
- El papel bond tiene un grosor de de pulgada por cien páginas. Escribe una ecuación para el ancho del libro, , si tiene cientos de páginas, impresas en papel bond.
- El papel Ledger tiene un grosor de pulgadas por cada cien páginas. Escribe una ecuación para el ancho del libro, , si tiene cientos de páginas, impresas en papel Ledger.
- Si, en cambio, se eligieran portadas y contraportadas de grosor de pulgada, ¿cómo cambiaría esto las ecuaciones de los dos puntos anteriores?