Lección 12Soluciones de ecuaciones lineales
Pensemos en lo que significa ser una solución de una ecuación lineal que tiene dos variables.
Metas de aprendizaje:
- Entiendo lo que es la solución de una ecuación en dos variables.
- Sé que la gráfica de una ecuación es una representación visual de todas las soluciones de la ecuación.
12.1 Estimemos el área
¿Cuál figura tiene el área sombreada más grande?

12.2 Manzanas y naranjas
En el mercado de la esquina, las manzanas cuestan $1 cada una y las naranjas cuestan $2 cada una.
- Halla el costo de:
- 6 manzanas y 3 naranjas
- 4 manzanas y 4 naranjas
- 5 manzanas y 4 naranjas
- 8 manzanas y 2 naranjas
-
Noah tiene $10 para gastar en el mercado. ¿Puede comprar 7 manzanas y 2 naranjas? Explica o muestra tu razonamiento.
-
¿Qué combinaciones de manzanas y naranjas puede comprar Noah si gasta todos sus $10?
-
Utiliza dos variables para escribir una ecuación que represente combinaciones de manzanas y naranjas que cuesten $10. Asegúrate de decir qué significa cada variable.
-
¿Cuáles 3 combinaciones de manzanas y naranjas hacen verdadera tu ecuación? ¿Cuáles tres combinaciones de manzanas y naranjas la hacen falsa?
¿Estás listo para más?
- Grafica la ecuación que escribiste para relacionar el número de manzanas y el número de naranjas.
- ¿Cuál es la pendiente de la gráfica? ¿Cuál es el significado de la pendiente en términos del contexto?
- Supongamos que Noah tiene $20 para gastar. Grafica la ecuación que describe esta situación. ¿Qué observas acerca de la relación que hay entre esta gráfica y la gráfica anterior?
12.3 Soluciones y todo lo demás
Tienes dos números. Si duplicas el primer número y lo sumas al segundo número, la suma es 10.
-
Digamos que representa al primer número y representa al segundo número. Escribe una ecuación que muestre la relación que hay entre , y 10.
-
Dibuja y etiqueta un par de ejes y . Ubica por lo menos cinco puntos en este plano de coordenadas que hagan verdadera la afirmación y tu ecuación. ¿Qué observas acerca de los puntos que ubicaste?
-
Haz una lista de diez puntos que no hagan verdadera la afirmación. Usa un color diferente para ubicar cada punto en el mismo plano de coordenadas. ¿Qué observas acerca de estos puntos en comparación con tu primer conjunto de puntos?
Resumen de la lección 12
Piensa en todos los rectángulos que tienen un perímetro de 8 unidades. Si representa el ancho y representa el largo, entonces la ecuación expresa la relación que hay entre el ancho y el largo de todos estos rectángulos.
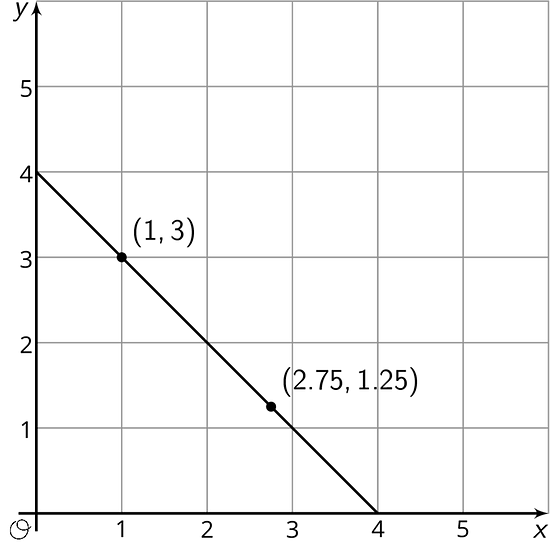
Por ejemplo, el ancho y el largo pueden ser 1 y 3, ya que o el ancho y el largo pueden ser 2.75 y 1.25, ya que .
Podemos hallar muchas otras parejas posibles de ancho y largo, , que hacen verdadera la ecuación, es decir, parejas que al ser sustituidas en la ecuación hacen que el lado izquierdo y el lado derecho sean iguales.
Una solución de una ecuación en dos variables es cualquier pareja de valores que hacen verdadera la ecuación.
Podemos pensar en las parejas de números que son soluciones de una ecuación como puntos en el plano de coordenadas. Esta es una recta formada por todos los puntos que son soluciones de la ecuación . Cada punto que está sobre la recta representa un rectángulo de perímetro 8 unidades. Todos los puntos que no están sobre la recta no son soluciones de la ecuación .
Términos del glosario
Una solución de una ecuación en dos variables es una pareja de valores para las variables que hacen que la ecuación sea verdadera.
Por ejemplo, una posible solución de la ecuación es . Al remplazar por 6 y por 0, la ecuación es verdadera porque .
Problemas de práctica de la lección 12
Selecciona todos los pares ordenados que sean soluciones de la ecuación lineal .
La gráfica muestra una relación lineal entre y .
representa el número de cómics que compra Priya en la tienda, todos al mismo precio, y representa la cantidad de dinero (en dólares) que tiene Priya después de comprar los cómics.
- Halla la intersección con el eje y la intersección con el eje de esta recta.
- Halla e interpreta la pendiente de esta recta.
- Halla una ecuación para esta recta.
- Si Priya compra 3 cómics, ¿cuánto dinero le quedará?
Empareja cada ecuación con sus tres soluciones.
- , ,
- , ,
- , ,
- , ,
- , ,
Un tanque de combustible dispensa combustible a una tasa de 5 galones por segundo. Si representa la cantidad de combustible que queda en el tanque y representa el número de segundos que han pasado desde que se empezó a dispensar combustible, entonces y satisfacen una relación lineal.
En el plano de coordenadas, ¿la pendiente de la recta que representa esta relación tendrá una pendiente positiva, negativa o cero? Explica cómo lo sabes.
Una tienda de sándwiches cobra una tarifa de domicilio para llevar el almuerzo a un edificio de oficinas. Una oficina paga $33 por 4 sándwiches de pavo. Otra oficina paga $61 por 8 sándwiches de pavo. ¿Cuánto suma cada sándwich de pavo al costo de la entrega? Explica cómo lo sabes.