Lección 4Comparemos relaciones proporcionales
Comparemos relaciones proporcionales.
Metas de aprendizaje:
- Puedo comparar relaciones proporcionales representadas de diferentes formas.
4.1 ¿Cuál es la relación?
La ecuación podría representar una variedad de situaciones diferentes.
-
Escribe una descripción de una situación representada por esta ecuación. Decide qué representan las cantidades y en tu situación.
-
Haz una tabla y una gráfica que representen la situación.
4.2 Trabajos de verano
-
Elena y Jada ganan dinero ayudando a sus vecinos.
Elena es niñera. Sus ganancias están dadas por la ecuación , donde representa la cantidad de horas que trabaja y representa la cantidad de dinero que gana.
Jada gana $7 por hora cortando el césped de sus vecinos.
- ¿Quién gana más dinero después de trabajar 12 horas? ¿Cuánto más gana? Explica cómo lo sabes.
- ¿Cuál es la tasa de cambio para cada situación y qué significa?
- ¿Cuánto tiempo le tomaría a cada persona ganar $150? Explica o muestra tu razonamiento.
-
Han y Clare tienen trabajos de verano diligenciando sobres para dos compañías diferentes.
Han gana $15 por cada 300 sobres que finaliza.
Ganancias de Clare:
cantidad de sobres dinero en dólares 400 40 900 90 - ¿Quién ganaría más dinero después de diligenciar 1,500 sobres? ¿Cuánto más dinero ganaría? Explica cómo lo sabes.
- ¿Cuál es la tasa de cambio para cada situación y qué significa?
- ¿A quién se le paga más en su trabajo? Explica o muestra tu razonamiento.
-
Tyler planea comenzar un puesto de limonada y está probando diferentes recetas de limonada. Él quiere asegurarse de que la receta no tenga demasiada mezcla de limonada (jugo de limón y azúcar) pero que aún tenga buen sabor.
La receta 1 viene dada por la ecuación , donde representa las tazas de la mezcla de limonada y representa las tazas de agua.
Receta 2:
mezcla de limonada (tazas) agua (tazas) 10 50 13 65 21 105 - Si Tyler tuviera 16 tazas de mezcla de limonada, ¿cuántas tazas de agua necesitaría para cada receta? Explica cómo lo sabes.
- ¿Cuál es la tasa de cambio para cada situación y qué significa?
- Tyler tiene una jarra de 5 galones (esto es 80 tazas) para usar en su puesto de limonada y 16 tazas de mezcla de limonada. ¿Qué receta de limonada debería usar? Explica o muestra tu razonamiento.
¿Estás listo para más?
Han y Clare todavía están llenando sobres. Han puede llenar 20 sobres en un minuto y Clare puede llenar 10 sobres en un minuto. Comienzan a trabajar juntos en una pila de 1,000 sobres.
- ¿Cuánto tardan en terminar la pila?
- ¿Quién gana más dinero?
Resumen de la lección 4
Cuando dos relaciones proporcionales se representan de diferentes maneras, las comparamos encontrando información común. Por ejemplo:
Las ganancias de Clare están representadas por la ecuación , donde es la cantidad de dinero que gana, en dólares, por trabajar horas.
La tabla muestra alguna información sobre el pago de Jada.
| tiempo trabajado (horas) | ganancias (dólares) |
|---|---|
| 7 | 92.75 |
| 4.5 | 59.63 |
| 37 | 490.25 |
¿A quién se le paga a una tasa más alta por cada hora? ¿Cuánto más gana esa persona después de 20 horas?
En la ecuación de Clare, vemos que la constante de proporcionalidad que relaciona sus ganancias con el tiempo trabajado es 14.50. Esto significa que gana $14.50 por cada hora.
Podemos calcular la constante de proporcionalidad de Jada dividiendo un valor en la columna de ganancias entre el valor de la misma fila en la columna de tiempo trabajado. Usando la última fila, la constante de proporcionalidad para Jada es 13.25, dado que . Una ecuación que representa las ganancias de Jada es . Esto significa que gana $13.25 por cada hora.
Entonces, a Clare se le paga a una tasa mayor que a Jada. Clare gana $1.25 más por cada hora que Jada, lo que significa que después de 20 horas de trabajo ella tiene más que Jada.
Problemas de práctica de la lección 4
Una contratista debe transportar una gran cantidad de tierra a un sitio de trabajo. Ella recogió información de dos empresas de transporte. "EZ Excavación" presenta sus precios en una tabla. "Transportadora Feliz" presenta sus precios en una gráfica.
tierra (yardas cúbicas) costo (dólares) 8 196 20 490 26 637 - ¿Cuánto cobraría cada empresa por transportar 40 yardas cúbicas de tierra? Explica o muestra tu razonamiento.
- Calcula la tasa de cambio para cada relación. ¿Qué significan para cada empresa?
- Si la contratista tiene 40 yardas cúbicas de tierra y un presupuesto de $1000, ¿qué compañía de transporte debería contratar? Explica o muestra tu razonamiento.
Andre y Priya están monitoreando la cantidad de pasos que caminan. Andre registra que puede caminar 6000 pasos en 50 minutos. Priya escribe la ecuación para describir su tasa de pasos, donde es la cantidad de pasos y es la cantidad de minutos que camina. Esta semana, Andre y Priya caminan cada uno un total de 5 horas. ¿Quién da más pasos? ¿Cuántos más?
Encuentra las coordenadas del punto en cada diagrama:
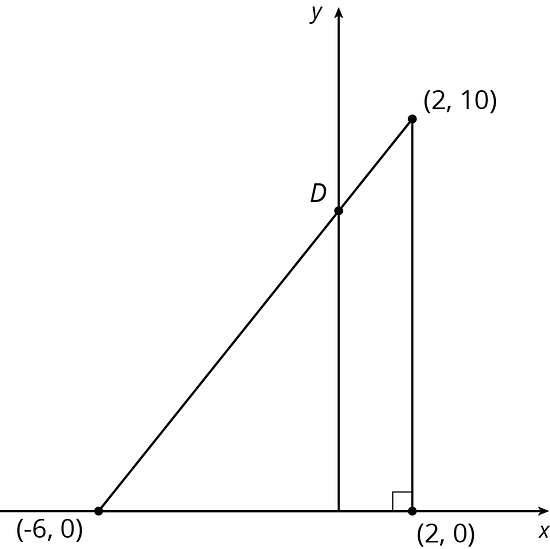
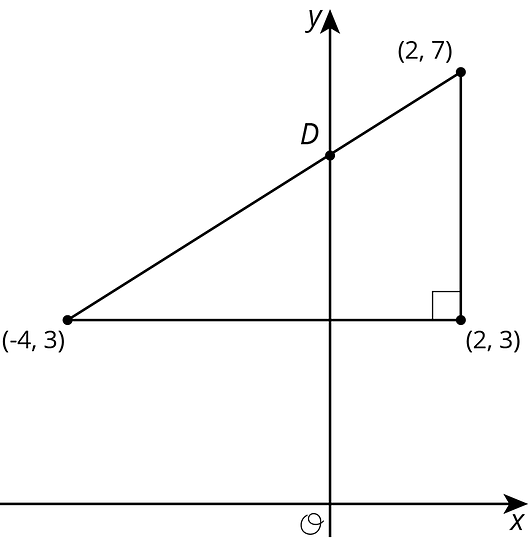
Selecciona todas las parejas de puntos para las cuales la recta entre esos puntos tiene una pendiente de .
- y
- y
- y
- y
- y