Lección 3Ecuaciones para funciones
Encontremos salidas de ecuaciones.
Metas de aprendizaje:
- Puedo encontrar la salida de una función si conozco la entrada.
- Puedo nombrar la variable independiente y la dependiente de una función dada y representar la función con una ecuación.
3.1 El área de un cuadrado
Llena la tabla de parejas de entrada y salida con la regla dada. En la caja del diagrama, escribe una expresión algebraica para esta regla.
| entrada | salida |
|---|---|
| 8 | |
| 2.2 | |
3.2 Diagramas, ecuaciones y descripciones
En la tabla, escribe las respuestas a estas preguntas:
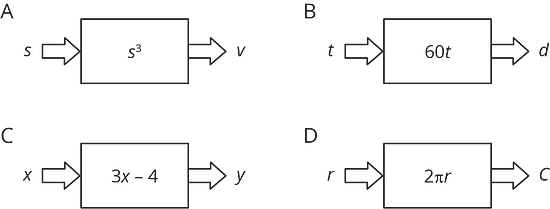
- Empareja cada una de estas descripciones con un diagrama:
- la circunferencia, , de un círculo con radio
- la distancia, , en millas que podrías recorrer en horas si manejas a 60 millas por hora
- la salida si triplicas la entrada y al resultado le restas 4
- el volumen, , de un cubo dada la longitud de su arista,
- Escribe una ecuación para cada descripción que exprese la salida como una función de la entrada.
- Para cada ecuación, encuentra la salida si la entrada es 5.
- Nombra la variable independiente y la dependiente de cada ecuación.
| descripción | a | b | c | d |
|---|---|---|---|---|
| diagrama | ||||
| ecuación | ||||
| entrada = 5 salida = ? |
||||
| variable independiente |
||||
| variable dependiente |
¿Estás listo para más?
Elige un número de 3 dígitos como entrada y aplícale la siguiente regla, un paso a la vez:
- Multiplica tu número por 7.
- Suma uno al resultado.
- Multiplica el resultado por 11.
- Resta 5 del resultado.
- Multiplica el resultado por 13.
- Resta 78 del resultado para obtener la salida.
¿Puedes describir una forma más simple de escribir esta regla? ¿Por qué esto funciona?
3.3 Monedas de 10 y de 25 centavos
Jada tenía algunas monedas de 10 centavos y otras de 25 centavos. En total tenía $12.50. La relación entre la cantidad de monedas de 10 centavos, , y la cantidad de monedas de 25 centavos, , se puede expresar con la ecuación .
- Si Jada tiene 4 monedas de 25 centavos, ¿cuántas monedas de 10 centavos tiene?
- Si Jada tiene 10 monedas de 25 centavos, ¿cuántas monedas de 10 centavos tiene?
- ¿El número de monedas de 10 centavos es una función del número de monedas de 25 centavos? Si lo es, escribe una regla (que comience con ...) que puedas usar para determinar la salida, , de una entrada dada, . Si no lo es, explica por qué no.
- Si Jada tiene 25 monedas de 10 centavos, ¿cuántas monedas de 25 centavos tiene?
- Si Jada tiene 30 monedas de 10 centavos, ¿cuántas monedas de 25 centavos tiene?
- ¿El número de monedas de 25 centavos es una función del número de monedas de 10 centavos? Si lo es, escribe una regla (que comience con ...) que puedas usar para determinar la salida, , de una entrada dada, . Si no lo es, explica por qué no.
Resumen de la lección 3
A veces podemos representar funciones con ecuaciones. Por ejemplo, el área () de un círculo es una función del radio () y podemos expresarla con una ecuación:
También podemos dibujar un diagrama para representar esta función:

En este caso, pensamos en el radio () como la entrada y en el área del círculo () como la salida. Por ejemplo, si la entrada es un radio de 10 cm, entonces la salida es un área de cm2, o aproximadamente 314 cm cuadrados. Como esta es una función, podemos encontrar el área () para cualquier radio () dado.
Como es la entrada, decimos que es la variable independiente y que la salida, , es la variable dependiente.
A veces, cuando tenemos una ecuación podemos elegir cuál variable es la variable independiente. Por ejemplo, si sabemos que
entonces, podemos pensar en como una función de y escribir
o podemos pensar en como una función de y escribir
Términos del glosario
Una variable dependiente representa la salida de una función.
Vamos a comprar 20 frutas y decidimos que serán manzanas y bananos. Si elegimos el número "" de manzanas primero, la ecuación nos dice el número "" de bananos que podemos comprar. El número de bananos es la variable dependiente porque depende del número de manzanas.
Una variable independiente es una cantidad que se usa para calcular otra cantidad. Una variable independiente representa la entrada de una función.
Vamos a comprar 20 frutas y decidimos que serán manzanas y bananos. Si elegimos el número "" de manzanas primero, la ecuación nos dice el número "" de bananos que podemos comprar. El número de manzanas es la variable independiente porque podemos elegir cualquier número como su valor.
Problemas de práctica de la lección 3
Esta es una ecuación que representa una función: .
Selecciona todas las diferentes ecuaciones que describen la misma función:
-
- Grafica un sistema de ecuaciones lineales que no tenga soluciones.
- Escribe una ecuación para cada recta que grafiques.
El arroz integral cuesta $2 por cada libra, y los frijoles cuestan $1.60 por cada libra. Lin tiene $10 para comprar estos artículos y hacer una gran comida de frijoles y arroz para una cena informal. es el número de libras de frijoles que Lin compra y es el número de libras de arroz que ella compra, cuando gasta todo su dinero en esta comida.
- Escribe una ecuación que relacione las dos variables.
- Reorganiza la ecuación para que sea la variable independiente.
- Reorganiza la ecuación para que sea la variable independiente.
Resuelve cada ecuación y comprueba tu respuesta.