Open Up Resources Logo

Lección 14Representaciones decimales de números racionales

Aprendamos más sobre cómo se pueden representar los números racionales.

Metas de aprendizaje:

  • Entiendo que todos los números tienen una expansión decimal.
  • Puedo escribir una fracción como un decimal que se repite.

14.1 Observa y pregúntate: barras sombreadas

¿Qué observas? ¿Qué te preguntas?

There are four rectangular bars of equal length, aligned vertically. The first rectangular bar is divided into two equal sized parts and the first part is shaded. The second rectangular bar is divided into 4 equal sized parts and the first part is shaded. The third rectangular bar is divided into 8 equal sized parts and the firts part is shaded. The fourth rectangular bar is divided into 16 equal sized parts and the first bar is shaded.

14.2 Partamos la longitud por la mitad

Esta es una recta numérica que va desde 0 hasta 1.

A number line with two tick marks, one on either end of the number line. The first tick mark is labeled "0" and the second tick mark is labeled "1."
  1. Marca el punto medio entre 0 y 1. ¿Cuál es la representación decimal de ese número?
  2. Marca el punto medio entre 0 y el último punto que marcaste. ¿Cuál es la representación decimal de ese número?
  3. Repite el paso dos. ¿Cómo hallaste el valor de este número?
  4. Describe cómo cambia el valor de los puntos medios que has agregado a la recta numérica a medida que hallas más. ¿Cómo cambian las representaciones decimales? 

14.3 Recalculemos números racionales

  1. Los números racionales son fracciones y sus opuestos. Todos estos números son números racionales. Muestra que son números racionales escribiéndolos en la forma  \frac{a}{b} o \text -\frac{a}{b} .

    1. 0.2
    2. \text -\sqrt{4}
    3. 0.333
    4. \sqrt[3]{1000}
    5. -1.000001
    6. \sqrt{\frac19}

  2. Todos los números racionales también tienen representaciones decimales. Halla la representación decimal de cada uno de estos números racionales.

    1. \frac38
    2. \frac75
    3. \frac{999}{1000}
    4. \frac{111}{2}
    5. \sqrt[3]{\frac18}

14.4 Acerquémonos a \frac{2}{11}

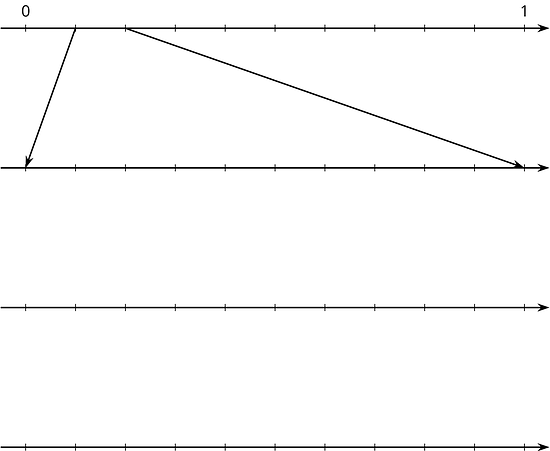
A zooming number line cosisting of 4 number lines, aligned vertically, each with 11 evenly spaced tick marks. On the first number line, the first tick mark is labeled "0" and the 11th tick mark is labeled "1." Two arrows are drawn from the first number line to the second number line. The first arrow is drawn from the second tick mark on the first number line to the first tick mark on the second number line. The second arrow is drawn from the third tick mark on the first number line to the eleventh tick mark on the second number line. There are no numbers inidicated on the second number line. The third and fourth number lines are both unlabeled.

  1. Etiqueta las marcas de la recta numérica que está más arriba. Después, halla la primera cifra decimal de  \frac{2}{11} utilizando división larga y estima dónde se debe ubicar  \frac{2}{11} sobre la primera recta numérica.

  2. Etiqueta las marcas de la segunda recta numérica. Halla la siguiente cifra decimal de  \frac{2}{11} continuando con la división larga y estima dónde se debe ubicar  \frac{2}{11} sobre la segunda recta numérica. Agrega flechas desde la segunda hasta la tercera recta numérica para hacer un acercamiento a la ubicación de  \frac{2}{11} .

  3. Repite el paso anterior para las rectas numéricas restantes.

  4. ¿Cuál crees que es la expansión decimal de  \frac{2}{11} ?

¿Estás listo para más?

Llamemos  x=\frac{25}{11}=2.272727 … y y=\frac{58}{33}=1.75757575 …

Para cada una de las siguientes preguntas, primero decide si es más útil la representación en forma de fracción o la representación decimal de los números para responder la pregunta y luego encuentra la respuesta.

  • ¿Cuál está más cerca de 2, x o  y ?
  • Halla x^2 .

Resumen de la lección 14

Anteriormente, aprendimos que los números racionales son una fracción o el opuesto de una fracción. Por ejemplo,  \frac34 y \text-\frac52 son números racionales. Una expresión numérica que se ve complicada también puede ser un número racional, siempre y cuando el valor de la expresión sea una fracción positiva o negativa. Por ejemplo,  \sqrt{64} y \text-\sqrt[3]{\frac18} son números racionales porque  \sqrt{64} = 8 y \text-\sqrt[3]{\frac18} = \text-\frac12 .

Los números racionales también se pueden escribir utilizando notación decimal. Algunos tienen expansiones decimales finitas, como 0.75, -2.5 o -0.5. Otros números racionales tienen expansiones decimales infinitas, como 0.7434343 . . . donde los 43 se repiten indefinidamente (por siempre). Para evitar escribir la parte que se repite una y otra vez, utilizamos la notación  0.7\overline{43} para este número. La barra que se encuentra sobre una parte de la expresión nos indica cuál es la parte que se repite indefinidamente.

La expansión decimal de un número nos ayuda a ubicarlo con precisión sobre una recta numérica que esté dividida en décimas. Por ejemplo,  0.7\overline{43} debe estar entre 0.7 y 0.8. Cada dígito decimal adicional aumenta la precisión de nuestra ubicación. Por ejemplo, el número  0.7\overline{43} está entre 0.743 y 0.744.

Problemas de práctica de la lección 14

  1. Andre y Jada discuten cómo escribir  \frac{17}{20} como un decimal.

    Andre dice que puede utilizar la división larga para dividir  17 entre 20 para obtener el decimal.

    Jada dice que puede escribir una fracción equivalente con un denominador de 100 al multiplicar por \frac{5}{5} , y luego escribir el número de centésimas como un decimal.

    1. ¿Ambas estrategias funcionan?

    2. ¿Cuál estrategia prefieres? Explica tu razonamiento.

    3. Escribe  \frac{17}{20} como un decimal. Explica o muestra tu razonamiento.

  2. Escribe cada fracción como un decimal.

    1. \sqrt{\frac{9}{100}}

    2. \frac{99}{100}

    3. \sqrt{\frac{9}{16}}

    4. \frac{23}{10}

  3. Escribe cada decimal como una fracción.

    1. \sqrt{0.81}

    2. 0.0276

    3. \sqrt{0.04}

    4. 10.01

  4. Halla la solución positiva de cada ecuación. Si la solución es irracional, escribe la solución utilizando la notación de raíz cuadrada o de raíz cúbica.

    1. x^2=90

    2. p^3=90

    3. z^2=1

    4. y^3=1

    5. w^2=36

    6. h^3=64

  5. Esta es una pirámide recta de base cuadrada.

    A right square pyramid. The side lengths of the square base are labeled 16. The slant height is labeled “L” and is indicated by a dashed line from the top vertex of the pyramid, along the middle of one of the side triangular faces. A right triangle is formed inside the pyramid by the slant height line, “L,” a dashed line from the top vertex of the pyramid, to the middle of the square, labeled 15, and by another dashed line that forms a right angle and connects along the base of the pyramid to the slant height, “L.” The slant height “L” is opposite the right angle.

    1. ¿Cuál es la medida de la altura inclinada \ell de la cara triangular de la pirámide? Si te estancas, utiliza una sección transversal de la pirámide.

    2. ¿Cuál es el área de superficie de la pirámide?