Open Up Resources Logo

Lección 3Números racionales e irracionales

Aprendamos sobre números irracionales.

Metas de aprendizaje:

  • Sé que es un número irracional y puedo dar un ejemplo.
  • Sé que es un número racional y puedo dar un ejemplo.

3.1 Conversación algebraica: soluciones positivas

Encuentra una solución positiva para cada ecuación: 

  1. x^2=36
  2. x^2=\frac94
  3. x^2=\frac14
  4. x^2=\frac{49}{25}

3.2 Tres cuadrados

Three blank square grids. Each grid has 2 rows of 2 squares.
  1. Dibuja 3 cuadrados de diferentes tamaños con vértices alineados a los vértices de la cuadrícula.

  2. Para cada cuadrado:

    1. Etiqueta el área.

    2. Etiqueta la longitud de lado.

    3. Escribe una ecuación que muestre la relación entre la longitud de lado y el área.

3.3 Busquemos una solución

¿Alguno de estos números es una solución a la ecuación x^2=2 ? Explica tu razonamiento.

  • 1

  • \frac12

  • \frac32

  • \frac75

3.4 Busquemos \sqrt2

Un número racional es una fracción o su opuesto (o cualquier número equivalente a una fracción o su opuesto).

  1. Encuentra más números racionales que estén cerca de \sqrt2 .
  2. ¿Puedes encontrar un número racional que sea exactamente \sqrt2 ?

¿Estás listo para más?

Si tienes una calculadora antigua evalúa la expresión \left(\frac{577}{408}\right)^2 y te dirá que la respuesta es 2, lo que podría llevarte a pensar que  \sqrt{2}=\frac{577}{408} .

  1. Explica por qué es sospechoso el resultado de la calculadora.
  2. Encuentra una explicación de por qué 408^2\boldcdot 2  no podría ser igual a 577^2 . ¿Cómo muestra esto que \left(\frac{577}{408}\right)^2  no podría ser igual a 2?
  3. Repite estas preguntas para \left(\frac{1414213562375}{10000000000000}\right)^2\neq 2, una ecuación en la que incluso muchas calculadoras y computadoras modernas se equivocarán.

Resumen de la lección 3

En una actividad previa, aprendimos que la notación de la raíz cuadrada se usa para escribir la longitud de lado de un cuadrado dada su área. Por ejemplo, un cuadrado cuya área es 2 unidades cuadradas tiene un lado de longitud de \sqrt{2}  unidades, lo que significa que  \sqrt{2} \boldcdot \sqrt{2} = 2.

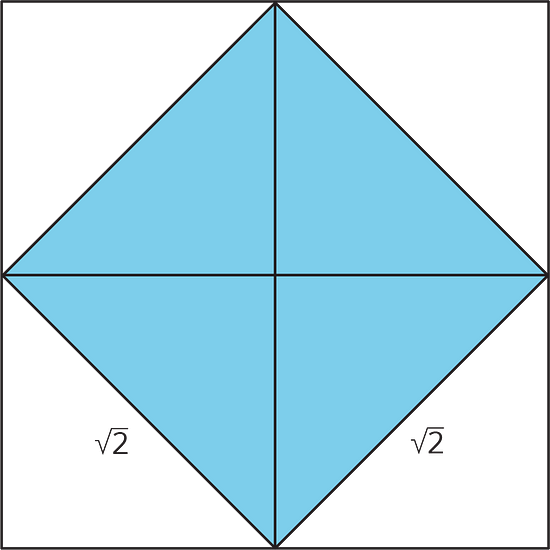
Un cuadrado cuya área es 25 unidades cuadradas tiene una longitud de lado de \sqrt{25}  unidades, lo que significa que  \sqrt{25} \boldcdot \sqrt{25} = 25. Dado que  5 \boldcdot 5 = 25 , sabemos que \sqrt{25}=5.

\sqrt{25}  es un ejemplo de un número racional. Un número racional es una fracción o su opuesto. Recuerda que una fracción \frac{a}{b}  es un punto en la recta numérica que se encuentra al dividir el segmento desde 0 a 1 en b  intervalos iguales y desplazarse a  de esos intervalos a la derecha desde 0. Siempre podemos escribir una fracción de la forma \frac{a}{b}  donde a  y b  son números enteros (y b  no es 0), pero hay otras formas de escribirlos. Por ejemplo, podemos escribir \sqrt{25} = \frac{5}{1} . Primero aprendiste sobre fracciones en grados anteriores y, en ese momento, probablemente no conocías los números negativos. Los números racionales son fracciones, pero pueden ser positivos o negativos. Entonces, -5 es también un número racional. Debido a que las fracciones y las razones son ideas estrechamente relacionadas, las fracciones y sus opuestos se denominan números racionales.

Estos son algunos ejemplos de números racionales: \frac{7}{4},\text{ } 0,\frac63, 0.2, \text-\frac{1}{3},\text-5, \sqrt{9},\text{ -}\frac{\sqrt{16}}{\sqrt{100}} ¿Puedes ver por qué son ejemplos de "una fracción o su opuesto"?   

Un número irracional es un número que no es racional. Es decir, es un número que no es una fracción o su opuesto. \sqrt{2}  es un ejemplo de un número irracional. Tiene una ubicación en la recta numérica, la cual puede aproximarse mediante números racionales (está justo a la derecha de \frac75 ); sin embargo,  \sqrt{2} no se puede encontrar en una recta numérica al dividir el segmento de 0 a 1 en b  partes iguales y desplazarse a  de esas partes a un lado de 0 (si a  y b  son números enteros).

A number line with 10 evenly spaced tick marks. The first tick mark is labeled 0 and the sixth tick mark is labeled 1. An arrow points to the eighth tick mark and is labeled seven-fifths. A second arrow points to a point slightly to the right of the eighth tick mark and is labeled the square root of 2.

\frac{17}{12}  también está cerca de \sqrt{2} , porque \left( \frac{17}{12} \right)^2=\frac{289}{144} . El número \frac{289}{144} está muy cerca de 2, ya que \frac{288}{144}=2 . Pero podríamos seguir buscando por siempre soluciones para x^2=2  que sean números racionales y no encontraríamos ninguna. ¡ \sqrt2 no es un número racional! Es irracional.

En tus estudios futuros, es posible que tengas la oportunidad de comprender o escribir una demostración de que \sqrt2  es irracional, pero por ahora simplemente demos por hecho que \sqrt2  es irracional. De manera similar, la raíz cuadrada de cualquier número entero o es un número entero ( \sqrt{36}=6 , \sqrt{64}=8 , etc.) o es un número irracional ( \sqrt{17} , \sqrt{65} , etc.). Estos son algunos otros ejemplos de números irracionales: \sqrt{10}, \text{ -}\sqrt3, \text{ }\frac{\sqrt5}{2},\text{ } \pi

Términos del glosario

número irracional

Un número irracional es un número que no es una fracción ni el opuesto de una fracción.

Pi ( \pi ) y \sqrt{2} son ejemplos de números irracionales.

número racional

Un número racional es una fracción o el opuesto de una fracción.

Algunos ejemplos de números racionales son: \frac74, 0, \frac63, 0.2, \text-\frac13, \text-5, \sqrt9

Problemas de práctica de la lección 3

  1. Decide si cada número en esta lista es racional o irracional. 

    \frac {\text{-}13}{3}, \text{ }0.1234, \text{ }\sqrt{37}, \text{ -} 77, \text{ -} \sqrt{100}, \text{ -} \sqrt{12}  

  2. ¿Qué valor es una solución exacta de la ecuación m^2=14 ?

    1. 7

    2. \sqrt{14}

    3. 3.74

    4. \sqrt{3.74}

  3. Un cuadrado tiene vértices  (0,0), (5,2), (3,7) , y  (\text-2,5) . ¿Cuál de las siguientes afirmaciones es verdadera?

    1. La longitud de lado del cuadrado es 5.

    2. La longitud de lado del cuadrado está entre 5 y 6.

    3. La longitud de lado del cuadrado está entre 6 y 7.

    4. La longitud de lado del cuadrado es 7.

  4. Reescribe cada una de las expresiones de una forma equivalente usando un solo exponente. 

    1. (10^2)^{\text-3}
    2. (3^{\text-3})^2
    3. 3^{\text-5} \boldcdot 4^{\text-5}
    4. 2^5 \boldcdot 3^{\text-5}

  5. La gráfica representa el área de hielo marino en el ártico en kilómetros cuadrados como una función del día del año, en 2016.

    1. Da un intervalo aproximado de días en el que el área de hielo marino en el ártico estuvo decreciendo.
    2. ¿En qué días el área de hielo marino en el ártico fue 12 millones de kilómetros cuadrados?

  6. Una preparatoria está organizando un evento para los estudiantes de último año pero se permitirá el ingreso de algunos estudiantes de primer año. El director aprobó el ingreso de 200 estudiantes al evento, y decidió que los estudiantes de primer año serían el 25% de los estudiantes de último año. ¿A cuántos estudiantes de último año se les permitirá asistir? Si tienes alguna dificultad, intenta escribir dos ecuaciones que representen el número de estudiantes de primer y último año en el evento.