Scaled Copies
This week your student will learn about scaling shapes. An image is a scaled copy of the original if the shape is stretched in a way that does not distort it. For example, here is an original picture and five copies. Pictures C and D are scaled copies of the original, but pictures A, B, and E are not.
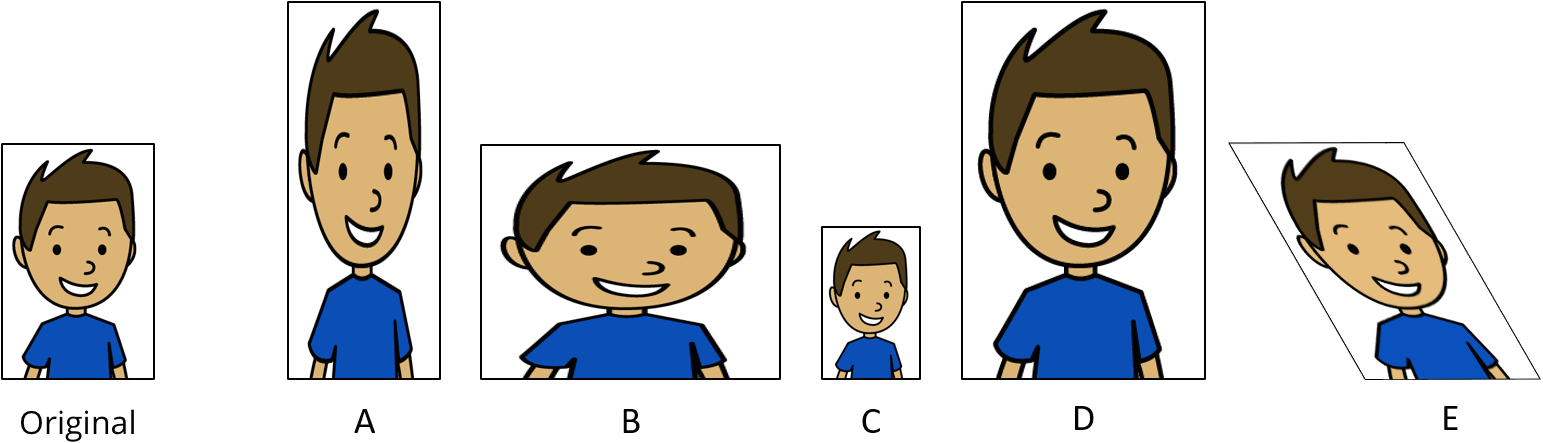
In each scaled copy, the sides are a certain number of times as long as the corresponding sides in the original. We call this number the scale factor. The size of the scale factor affects the size of the copy. A scale factor greater than 1 makes a copy that is larger than the original. A scale factor less than 1 makes a copy that is smaller.
Here is a task to try with your student:
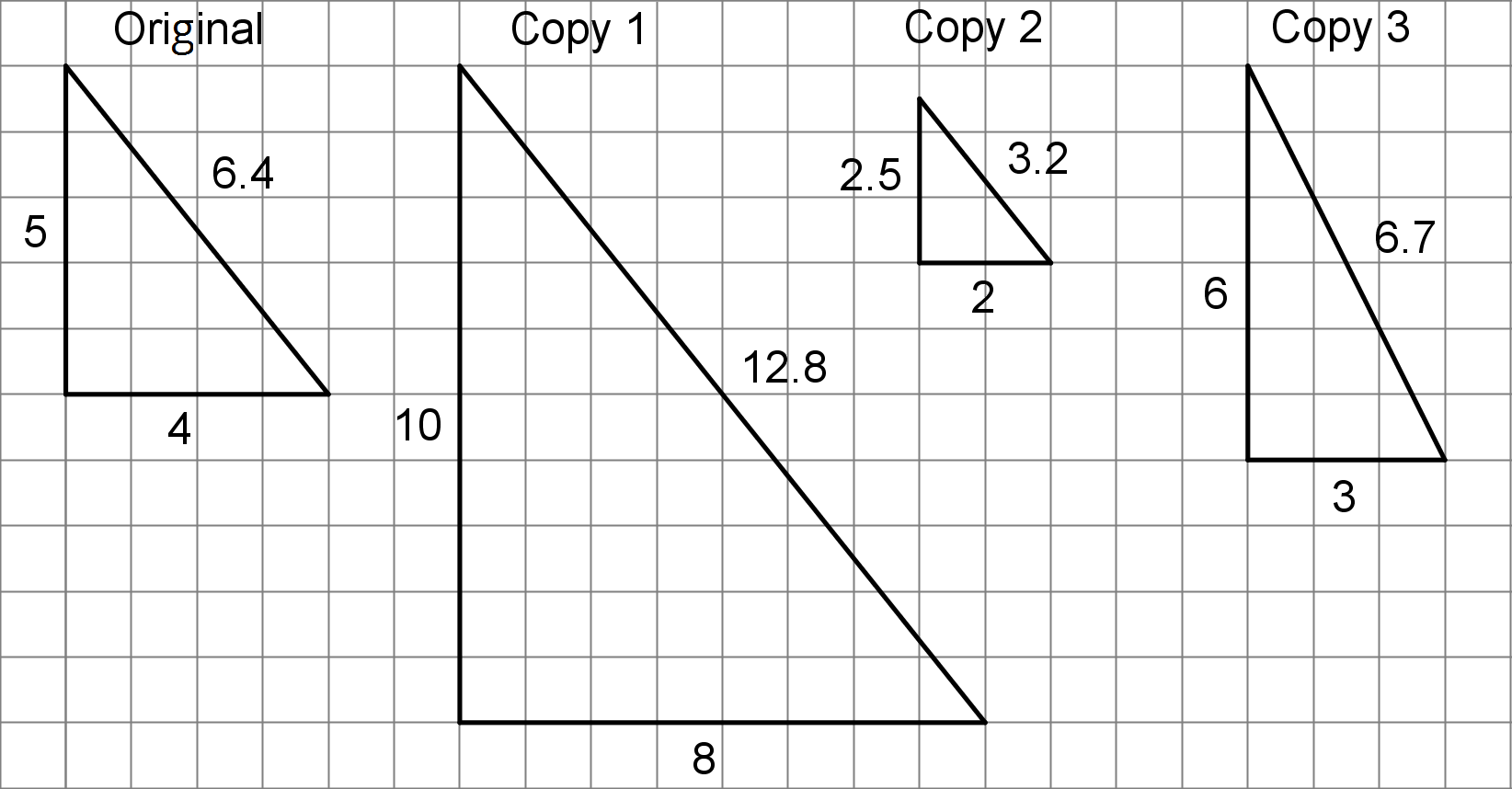
- For each copy, tell whether it is a scaled copy of the original triangle. If so, what is the scale factor?
- Draw another scaled copy of the original triangle using a different scale factor.
Solution:
-
- Copy 1 is a scaled copy of the original triangle. The scale factor is 2, because each side in Copy 1 is twice as long as the corresponding side in the original triangle. 5 \boldcdot 2 = 10, 4 \boldcdot 2 = 8, (6.4) \boldcdot 2 = 12.8
- Copy 2 is a scaled copy of the original triangle. The scale factor is \frac12 or 0.5, because each side in Copy 2 is half as long as the corresponding side in the original triangle. 5 \boldcdot (0.5) = 2.5, 4 \boldcdot (0.5) = 2, (6.4) \boldcdot (0.5) = 3.2
- Copy 3 is not a scaled copy of the original triangle. The shape has been distorted. The angles are different sizes and there is not one number we can multiply by each side length of the original triangle to get the corresponding side length in Copy 3.
- Answers vary. Sample response: A right triangle with side lengths of 12, 15, and 19.2 units would be a scaled copy of the original triangle using a scale factor of 3.
Scale Drawings
This week your student will be learning about scale drawings. A scale drawing is a two-dimensional representation of an actual object or place. Maps and floor plans are some examples of scale drawings.

The scale tells us what some length on the scale drawing represents in actual length. For example, a scale of “1 inch to 5 miles” means that 1 inch on the drawing represents 5 actual miles. If the drawing shows a road that is 2 inches long, we know the road is actually 2 \boldcdot 5, or 10 miles long.
Scales can be written with units (e.g. 1 inch to 5 miles), or without units (e.g., 1 to 50, or 1 to 400). When a scale does not have units, the same unit is used for distances on the scale drawing and actual distances. For example, a scale of “1 to 50” means 1 centimeter on the drawing represents 50 actual centimeters,1 inch represents 50 inches, etc.
Here is a task to try with your student:
Kiran drew a floor plan of his classroom using the scale 1 inch to 6 feet.
- Kiran's drawing is 4 inches wide and 5\frac12 inches long. What are the dimensions of the actual classroom?
- A table in the classroom is 3 feet wide and 6 feet long. What size should it be on the scale drawing?
- Kiran wants to make a larger scale drawing of the same classroom. Which of these scales could he use?
- 1 to 50
- 1 to 72
- 1 to 100
Solution:
- 24 feet wide and 33 feet long. Since each inch on the drawing represents 6 feet, we can multiply by 6 to find the actual measurements. The actual classroom is 24 feet wide because 4 \boldcdot 6 = 24. The classroom is 33 feet long because 5\frac12 \boldcdot 6 = 5 \boldcdot 6 + \frac12 \boldcdot 6 = 30 + 3 = 33.
- \frac12 inch wide and 1 inch long. We can divide by 6 to find the measurements on the drawing. 6 \div 6 = 1 and 3 \div 6 = \frac12.
- A, 1 to 50. The scale “1 inch to 6 feet” is equivalent to the scale “1 to 72,” because there are 72 inches in 6 feet. The scale “1 to 100” would make a scale drawing that is smaller than the scale “1 to 72,” because each inch on the new drawing would represent more actual length. The scale “1 to 50” would make a scale drawing that is larger than the scale “1 to 72,” because Kiran would need more inches on the drawing to represent the same actual length.