Lección 7Sumar y restar para resolver problemas
Apliquemos lo que sabemos acerca de números con signo a diversas situaciones.
Metas de aprendizaje:
- Puedo resolver problemas que involucran suma y resta de números racionales.
7.1 ¿Positivo o negativo?
Sin cálculos:
- ¿La solución para es positiva o negativa?
-
¿Cuáles de las siguientes opciones son soluciones para ?
7.2 Inventario de teléfonos
Un almacén registra el número de teléfonos celulares que tiene en inventario y cuántos teléfonos celulares vende. La tabla muestra el inventario para un modelo de teléfono al comienzo de cada día de la semana pasada. El inventario cambia cuando venden teléfonos o reciben entregas de teléfonos en el almacén.
| inventario | cambio | |
|---|---|---|
| Lunes | 18 | -2 |
| Martes | 16 | -5 |
| Miércoles | 11 | -7 |
| Jueves | 4 | -6 |
| Viernes | -2 | 20 |
- ¿Qué crees que significa que el cambio sea positivo?, ¿que sea negativo?
- ¿Qué crees que significa que el inventario sea positivo?, ¿que sea negativo?
- Basándonos en la información de la tabla, ¿cuál crees que será el inventario el sábado en la mañana? Explica tu razonamiento.
- ¿Cuál es la diferencia entre el mayor inventario y el menor inventario?
7.3 Energía solar
La familia de Han adquirió un panel solar. Cada mes, ellos obtienen un crédito en su cuenta por la electricidad que es generada por el panel solar. El crédito que ellos reciben varía de acuerdo a qué tan soleado está.

En enero usaron $83.56 de electricidad y generaron $6.75 de electricidad. Esta es su factura de electricidad para enero.
Cargos actuales: $83.56
Crédito solar: -$6.75
Cantidad a pagar: $76.81
- En julio, ellos viajaron lejos de casa y solo usaron $19.24 de electricidad. Su panel solar generó $22.75 de electricidad. ¿Cuál fue la cantidad a pagar en julio?
-
La tabla muestra el valor de la electricidad que usaron y el valor de la electricidad que generaron cada semana durante un mes. ¿Cuál es la cantidad a pagar para este mes?
usado ($) generado ($) semana 1 13.45 -6.33 semana 2 21.78 -8.94 semana 3 18.12 -7.70 semana 4 24.05 -5.36 - ¿Cuál es la diferencia entre el valor de la electricidad generada en la semana 1 y la semana 2?, ¿entre la semana 2 y la semana 3?
¿Estás listo para más?
7.4 Diferencias y distancias
Ubica estos puntos en el plano de coordenadas:
- ¿Qué figura se forma si conectas los puntos en orden?
- ¿Cuáles son las longitudes de los lados de la figura ?
- ¿Cuál es la diferencia entre las coordenadas de y ?
- ¿Cuál es la diferencia entre las coordenadas de y ?
- ¿Cómo se relacionan las diferencias de las coordenadas con las distancias entre los puntos?
Resumen de la lección 7
Algunas veces usamos números positivos y negativos para representar cantidades en un contexto determinado. Estos son algunos contextos que hemos estudiado que se pueden representar con números positivos y negativos:
- temperatura
- altitud
- inventario
- saldo en una cuenta
- electricidad entrante y saliente
En estas situaciones usar números positivos y negativos, y operaciones con números positivos y negativos nos ayuda a entenderlos y analizarlos. Para resolver problemas en estas situaciones, solo tenemos que entender qué significa que la cantidad sea positiva o negativa, y qué significa sumarlas y restarlas.
Cuando dos puntos en el plano de coordenadas están sobre una recta horizontal, puedes encontrar la distancia entre ellos al restar sus coordenadas .
Cuando dos puntos en el plano de coordenadas están sobre una recta vertical, puedes encontrar la distancia entre ellos al restar sus coordenadas .
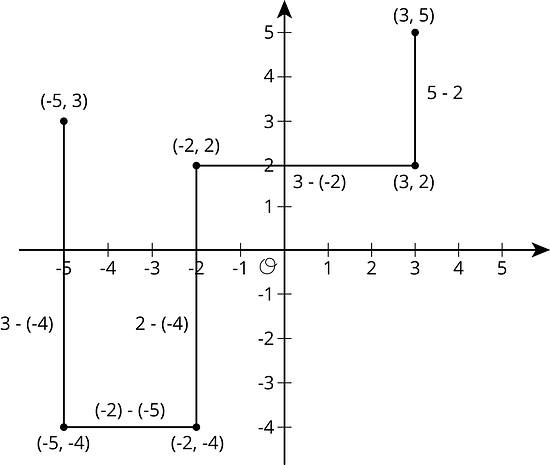
Recuerda: la distancia entre dos números es independiente del orden, pero la diferencia depende del orden.
Problemas de práctica de la lección 7
Tyler ordena una comida que cuesta $15.
- Si la tasa de impuesto es 6.6%, ¿cuánto será el impuesto de venta de la comida de Tyler?
- Tyler también quiere dejar una propina para el mesero. ¿Cuánto crees que debería pagar en total? Explica tu razonamiento.
En un videojuego, un personaje se cura a una tasa constante mientras permanezca parado en un círculo en particular. Completa la tabla.
tiempo en el círculo
(segundos)salud obtenida
(puntos)4 100 10 3 1,000 - ¿Cuánto más alto es 500 m que 400 m?
- ¿Cuánto más alto es 500 m que -400 m?
- ¿Cuál es el cambio en altitud desde 8,500 m a 3,400 m?
- ¿Cuál es el cambio en altitud entre 8,500 m y -300 m?
- ¿Cuánto más alto es -200 m que 450 m?
La tabla muestra cuatro transacciones y el saldo de cuenta en una cuenta bancaria, aunque algunos números hacen falta. Completa los números que faltan.
cantidad de la transacción saldo en la cuenta transacción 1 360 360 transacción 2 -22.50 337.50 transacción 3 182.35 transacción 4 -41.40 La desviación del promedio es la diferencia entre la cantidad real de lluvia y la cantidad promedio de lluvia para un mes determinado.
El promedio histórico de lluvia en Albuquerque, NM para junio, julio y agosto se muestra en la tabla.
Junio Julio Agosto 0.67 1.5 1.57 - En junio pasado, cayeron solo 0.17 pulgadas de lluvia durante todo el mes. ¿Cuál es la diferencia entre el promedio de lluvias y la lluvia real en junio pasado?
- La desviación del promedio de lluvias en julio pasado fue -0.36 pulgadas. ¿Cuánto llovió en julio pasado?
- ¿Cuánta lluvia tendría que caer en agosto para que la cantidad total de lluvia iguale el promedio de lluvias para estos tres meses? ¿Cuál sería la desviación del promedio en agosto en esta situación?