Open Up Resources Logo

Lección 8Posición, rapidez y dirección

Usemos números con signo para representar movimiento.

Metas de aprendizaje:

  • Puedo multiplicar un número positivo con un número negativo.
  • Puedo usar números racionales para representar rapidez y dirección.

8.1 Distancia, tasa, tiempo

  1. Un avión se mueve a una rapidez constante de 120 millas por hora durante 3 horas. ¿Cuánto avanza?
  2. Un tren se mueve a una rapidez constante y recorre 6 millas en 4 minutos. ¿Cuál es su rapidez en millas por minuto?
  3. Un automóvil se mueve a una rapidez constante de 50 millas por hora. ¿Cuánto tarda el automóvil en recorrer 200 millas?

8.2 Hacia la izquierda, hacia la derecha

A blank number line. The numbers negative 24 through 24, in increments of two, are indicated. There are tick marks midway between.
  1. Después de cada movimiento, anota tu ubicación en la tabla. Después, escribe una expresión para representar la posición final que use la posición inicial, la rapidez y el tiempo. La primera fila ya se ha completado.
    posición
    inicial    		 dirección rapidez
    (unidades por
    segundo)    		 tiempo
    (segundos)    		 posición
    final
    (unidades)    		 expresión
    0 derecha 5 3 +15 0 + 5 \boldcdot 3
    0 izquierda 4 6
    0 derecha 2 8
    0 derecha 6 2
    0 izquierda 1.1 5
  2. ¿Cómo puedes ver la dirección del movimiento en la expresión?
  3. Usando una posición inicial  p , una rapidez s  y un tiempo t , escribe dos expresiones para un punto final. Una expresión debe mostrar el resultado de moverse a la derecha y una expresión debe mostrar el resultado de moverse a la izquierda.

8.3 Velocidad

Una ingeniera de seguridad vial estaba estudiando patrones de desplazamiento en una autopista. Ella configuró una cámara y grabó la rapidez y dirección de los automóviles y camiones que pasaban frente a la cámara. Las posiciones al este de la cámara son positivas y al oeste son negativas.

A number line with 3 evenly spaced tick marks. Starting with the first tick mark, the numbers negative 100, 0 and 100 are indicated. The leftmost side is labeled “west.” The rightmost side is labeled “east.”

Los vehículos que viajan hacia el este tienen una velocidad positiva y los vehículos que viajan hacia el oeste tienen una velocidad negativa.

  1. Completa la tabla con la posición de cada vehículo, suponiendo que el vehículo viaja a una rapidez constante durante el período de tiempo indicado. Luego escribe una ecuación.
    velocidad
    (metros por
    segundo)    		 tiempo después
    de pasar frente
    a la cámara
    (segundos)    		 posición
    final
    (metros)    		 ecuación que
    describe la
    posición
    +25 +10 +250 25 \boldcdot 10 = 250
    -20 +30
    +32 +40
    -35 +20
    +28 0
  2. Si un automóvil está viajando al este cuando pasa frente a la cámara, ¿su posición será positiva o negativa 60 segundos después de que pase la cámara? Si multiplicamos dos números positivos, ¿el resultado es positivo o negativo?
  3. Si un automóvil está viajando al oeste cuando pasa frente a la cámara, ¿su posición será positiva o negativa 60 segundos después de que pase la cámara? Si multiplicamos un número positivo y uno negativo, ¿el resultado es positivo o negativo?

¿Estás listo para más?

En muchos contextos podemos interpretar tasas negativas como "tasas en la dirección opuesta". Por ejemplo, un automóvil que viaja a -35 millas por hora está desplazándose en la dirección opuesta de un automóvil que viaja a 40 millas por hora.

  1. ¿Qué podría significar si decimos que el agua está fluyendo a una tasa de -5 galones por minuto? 
  2. Inventa otra situación usando una tasa negativa y explica lo que esto podría significar.

Resumen de la lección 8

Podemos usar números con signo para representar la posición de un objeto sobre una recta. Seleccionamos un punto como el punto de referencia y lo llamamos cero. Las posiciones a la derecha del cero son positivas. Las posiciones a la izquierda del cero son negativas.

A number line with the numbers negative 10 through 10 indicated. A point is indicated at zero and is labeled "reference point." Another point is indicated at negative 4 and is labeled "4 units to the left of zero." A third point is indicated at 7 and is labeled "7 units to the right of zero."

Cuando se combina rapidez con dirección, indicada por el signo del número, esta se llama velocidad. Por ejemplo, si nos estamos moviendo 5 metros por segundo hacia la derecha, entonces la velocidad es +5 metros por segundo. Si nos estamos moviendo 5 metros por segundo hacia la izquierda, entonces la velocidad es -5 metros por segundo.

Si comenzamos en cero y nos movemos 5 metros por segundo durante 10 segundos, estaremos 5\boldcdot 10= 50 metros a la derecha del cero. En otras palabras, 5\boldcdot 10 = 50 .

Si comenzamos en cero y nos movemos -5 metros por segundo durante 10 segundos, estaremos -5\boldcdot 10= 50 metros a la izquierda del cero. En otras palabras,

\text-5\boldcdot 10 = \text-50

En general, un número negativo multiplicado por un número positivo es un número negativo.

Problemas de práctica de la lección 8

  1. Una recta numérica puede representar posiciones que están al norte y al sur de una parada de camiones. Decide si quieres que las posiciones positivas estén al norte o al sur de la parada de camiones. Luego, grafica las siguientes posiciones en la recta numérica.

    1. La parada de camiones
    2. 5 millas al norte de la parada de camiones
    3. 3.5 millas al sur de la parada de camiones
    1. ¿Cómo podrías diferenciar entre desplazarse al oeste a 5 millas por hora y desplazarse al este a 5 millas por hora sin usar las palabras "este" u "oeste"?
    2. Cuatro personas están montando en bicicleta. Cada uno comienza en el mismo lugar (0 representa su punto inicial). Grafica sus posiciones finales después de cinco segundos de montar en bicicleta, en una recta numérica.
      • Lin anda a 5 metros por segundo
      • Diego anda a -4 metros por segundo
      • Elena anda a 3 metros por segundo
      • Noah anda a -6 metros por segundo

  3. Encuentra el valor de cada expresión.

    16.2 + \text-8.4

    \frac25 - \frac35

    \text-9.2 + \text-7

    (\text-4\frac38) - (\text-1\frac14)

  4. Un cliente compró una sandía, un paquete de servilletas y algunos platos de papel. En su estado, no hay impuestos sobre la comida. La tasa de impuestos sobre los artículos que no son comida es del 5%. El total de los tres artículos que compró fue de $8.25 sin impuestos y pagó $0.19 en impuestos. ¿Cuánto costó la sandía?

  5. Para cada pregunta, escribe dos ecuaciones más que usen los mismos números y que expresen la misma relación de una manera diferente.

    1. 3 + 2 = 5
    2. 7.1 + 3.4 = 10.5
    3. 15 - 8 = 7
    4. \frac32 + \frac95 = \frac{33}{10}

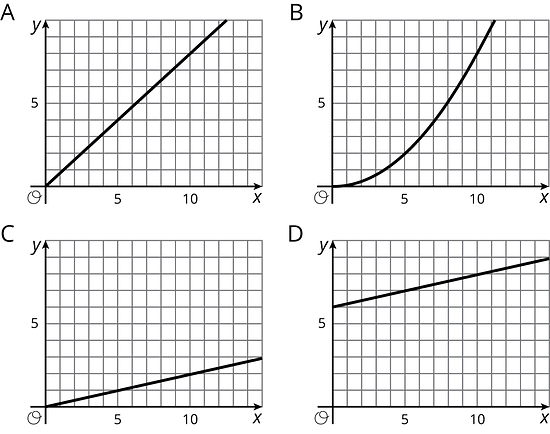
  6. ¿Qué gráficas no podrían representar una relación proporcional? Explica cómo lo decidiste.

    Four graphs of curves labeled A, B, C, and D in the xy coordinate plane with the origin labeled “O”. For each graph, the x axis has the numbers 0, 5, and 10 indicated. The y axis has the numbers 0 and 5. In graph A, the curve is a line that begins at the origin and moves steadily upward and to the right. In graph B, the curve begins at the origin and moves upward and to the right. It moves slowly in the beginning and then goes steeply upward. In graph C, the curve is a line that begins at the origin and moves slowly upward and to the right. In graph D, the curve is a line that begins on the vertical axis and above the origin. It moves slowly upward and to the right.