Open Up Resources Logo

Lección 7Una demostración del teorema de Pitágoras

Demostremos el teorema de Pitágoras.

Metas de aprendizaje:

  • Puedo explicar por qué el teorema de Pitágoras es verdadero.

7.1 Observa y pregúntate: un cuadrado y cuatro triángulos

¿Que observas? ¿Qué te preguntas?

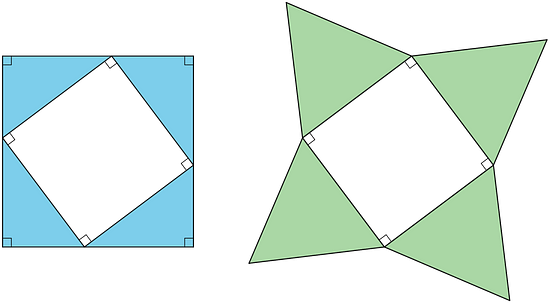
7.2 Sumemos áreas

Las dos figuras que se muestran a continuación son cuadrados con una longitud de lado de a + b . Observa que la primera figura se divide en dos cuadrados y dos rectángulos. La segunda figura está dividida en un cuadrado y cuatro triángulos rectángulos con catetos de longitud a  y b . Llamemos a la hipotenusa de estos triángulos c .

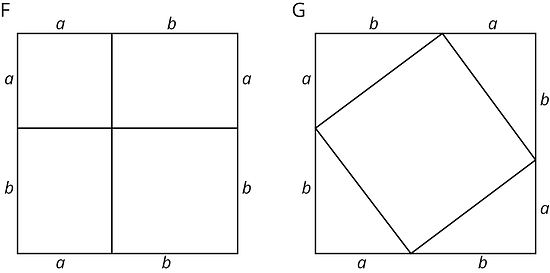
Two squares of the same area are labeled “F” and “G”. Square F is divided into the following: A square with side lengths “a”. Two rectangles with side lengths “a” and “b”. A square with side lengths “b”. Square G is divided into the following: Four identical triangles on each corner of the square with sides labeled “a” and “b”. A square in the center with unlabeled side lengths.
  1. ¿Cuál es el área total de cada figura?
  2. Encuentra el área de cada una de las 9 regiones más pequeñas que se muestran en las figuras y márcalas sobre el dibujo.
  3. Suma el área de las cuatro regiones de la figura F y suma el área de las cinco regiones de la figura G. Plantea una ecuación igualando estas dos expresiones. Si reescribes esta ecuación usando la menor cantidad de términos posible, ¿qué obtienes?

¿Estás listo para más?

Toma un triángulo rectángulo con lados 3-4-5, agrega los cuadrados de las longitudes de los lados y forma un hexágono que una los vértices de los cuadrados como en la imagen. ¿Cuál es el área de este hexágono?

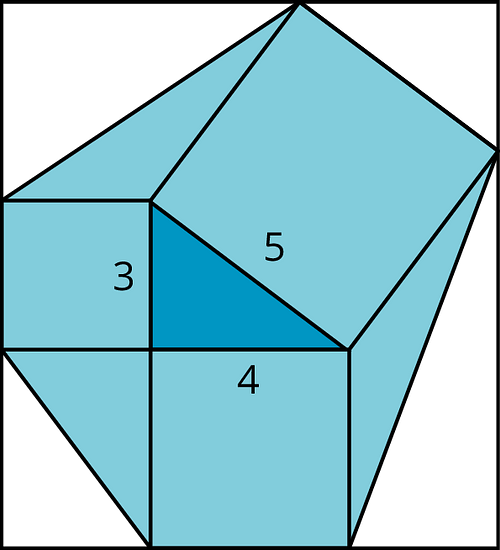
7.3 Utilicemos esta nueva herramienta

Encuentra las longitudes de lado desconocidas de estos triángulos rectángulos.

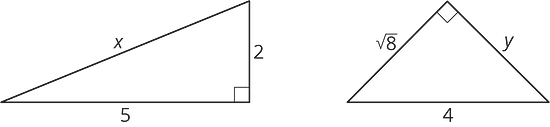
7.4 Una demostración con transformaciones

Usa los applets para explorar la relación entre áreas.

  • Considera los cuadrados A y  B .

  • Marca la casilla para ver el área dividida en cinco partes con dos segmentos.

  • Marca la casilla para ver las piezas.

  • Organiza las cinco piezas para que quepan dentro del cuadrado C .

  • Marca la casilla para ver el triángulo rectángulo.

  • Organiza las figuras para que los cuadrados sean adyacentes a los lados del triángulo.
  1. Si el triángulo rectángulo tiene catetos a  y b  e hipotenusa c , ¿qué has demostrado que es verdadero?
abrir en modo presentación
  1. Inténtalo de nuevo con diferentes cuadrados. Calcula las áreas de los nuevos cuadrados, A , B y  C  y explica lo que observas.
abrir en modo presentación
  1. Calcula las áreas de estos nuevos cuadrados  A , B y  C y luego explica lo que observas a medida que completas la actividad.
abrir en modo presentación

4. ¿Qué crees que podamos concluir?

Resumen de la lección 7

Las figuras que se muestran a continuación se pueden usar para ver por qué el teorema de Pitágoras es verdadero. Ambos cuadrados grandes tienen la misma área, pero se dividen de diferentes maneras. (¿Puedes ver dónde están ubicados los triángulos del Cuadrado G en el Cuadrado F? ¿Qué quiere decir eso con respecto a los cuadrados que están adentro de F y G?). Cuando se establece que la suma de las cuatro áreas que se encuentran en el Cuadrado F es igual a la suma de las 5 áreas que se encuentran en el Cuadrado G, el resultado es que a^2 + b^2 = c^2 , donde c  es la hipotenusa de los triángulos en el Cuadrado G y también la longitud del lado del cuadrado que se encuentra en el centro. ¡Inténtalo!

Two squares of the same area are labeled “F” and “G”. Square F is divided into the following: A square with side lengths “a”. Two rectangles with side lengths “a” and “b”. A square with side lengths “b”. Square G is divided into the following: Four identical triangles on each corner of the square with sides labeled “a” and “b”. A square in the center with unlabeled side lengths.

Esto es cierto para cualquier triángulo rectángulo. Si los catetos son a  y b  y la hipotenusa es c , entonces a^2+b^2=c^2 . Esta propiedad se puede utilizar en cualquier oportunidad en la podamos hacer un triángulo rectángulo. Por ejemplo, para encontrar la longitud de este segmento de recta:

A line segment slanted downward and to the right on a square grid. The bottom endpoint is 7 units down and 24 units to the right from the top endpoint.

La cuadrícula se puede usar para hacer un triángulo rectángulo, donde el segmento de recta es la hipotenusa y los catetos miden 24 unidades y 7 unidades:  

A right triangle on a square grid. The horizontal side has a length of 24 and the vertical side has a length of 7. The hypotenuse is labeled c.

Dado que este es un triángulo rectángulo, 24^2+7^2=c^2 . La solución a esta ecuación (y la longitud del segmento de recta) es c=25 .

Problemas de práctica de la lección 7

    1. Encuentra las longitudes de los lados sin marcar. 
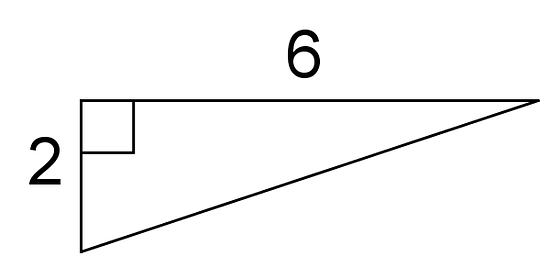
      A right triangle with a horizontal side on the top and a vertical side on the left. The top side is labeled 6 and the side on the left is labeled 2.
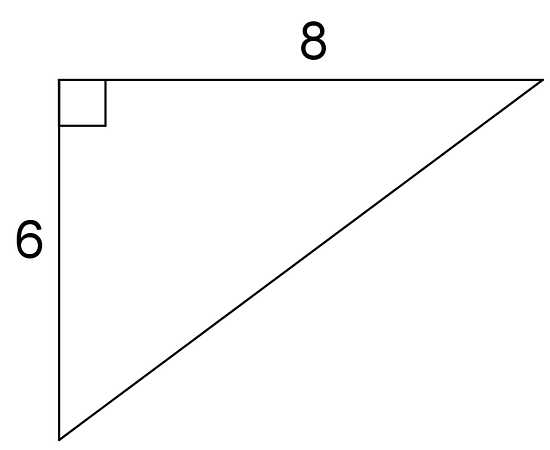
      A right triangle with a horizontal side on top and a vertical side on the left. The top side is labeled 8 and the left side is labeled 6.
    2. Un segmento tiene n unidades de largo y el otro tiene p unidades de largo. Encuentra el valor de  n y  p . (Cada cuadrado de la cuadrícula pequeña es 1 unidad cuadrada). 
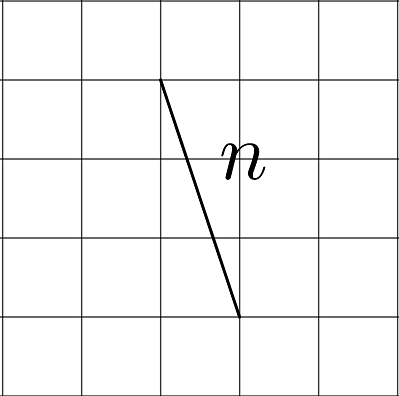
      A line segment labeled “n” on a square grid. The line segment starts at an intersection point on the grid and slants downward and to the right to an end point that is 1 unit to the right and 3 units down.
      A line segment labeled “p” on a square grid. The line segment starts at an intersection point on the grid and slants upward and to the right to an end point that is 3 units to the right and 4 units up.

  2. Utiliza las área de los dos cuadrados idénticos para explicar por qué 5^2+12^2=13^2 sin hacer ningún cálculo. 

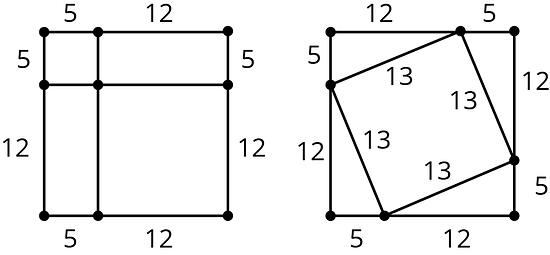
  3. ¿Entre cuáles dos números enteros consecutivos se encuentra cada número? 

    1. \sqrt{10}

    2. \sqrt{54}

    3. \sqrt{18}

    4. \sqrt{99}

    5. \sqrt{41}

    1. Da un ejemplo de un número racional y explica cómo sabes que es racional.

    2. Da tres ejemplos de números irracionales.

  5. Escribe cada expresión como una sola potencia de 10.

    1. 10^5 \boldcdot 10^0
    2. \frac{10^9}{10^0}

  6. Andre debe pedir cinta para hacer las decoraciones en un evento escolar. Él necesita exactamente 50.25 metros de cinta azul y verde. Andre necesita un 50% más de cinta azul que de cinta verde para el diseño básico, más 6.5 metros adicionales de cinta azul para los detalles. ¿Cuántos metros de cinta de cada color necesita Andre?