Section C: Practice Problems Angle Analysis
Section Summary
Details
Earlier in the unit, we learned that a right angle measures exactly
-
Acute angles are less than 90º.
-
Obtuse angles are greater than 90º but less than 180º.
-
Straight angles are exactly 180º.
We also solved problems about angles. For example, if two angles make a right angle or a straight angle, we can use the size of one angle to find the other.
The shaded angle here must be
Another example: Knowing that a full turn measures
a
angle every hour a
angle every one-half hour a
angle every 15 minutes a
angle every 10 minutes
Problem 1 (Lesson 12)
Draw an acute angle. Explain how you know the angle is acute.
Extend one of the rays of your angle in the opposite direction. Explain why you’ve now created a new angle that is obtuse.
Problem 2 (Lesson 13)
The circle is divided into 12 equal parts. What is the measure of angle
? Explain or show how you know.
Can you put together
angles to make a circle? How many of them will it take?
Problem 3 (Lesson 13)
A circle has been cut into eighths. How many degrees is the angle labeled
? Explain or show your reasoning. 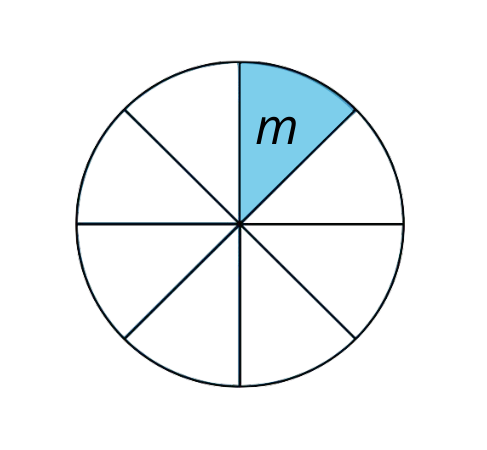
Another circle has been cut into fifths. How many degrees is the angle labeled
? Explain or show your reasoning. 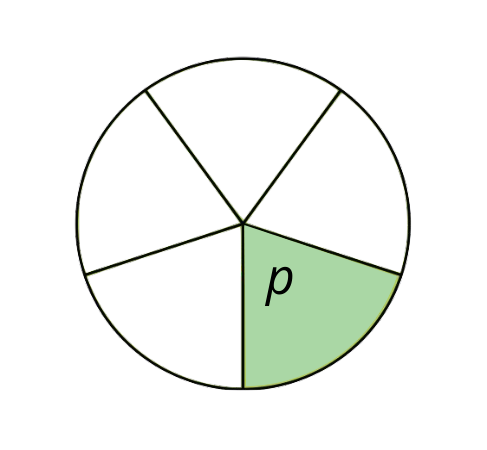
Problem 4 (Lesson 13)
What is the measure of each angle
? Explain or show how you know. How many
angles can you fit together at one vertex without gaps or overlaps?
Problem 5 (Lesson 14)
What angles are made by the hour and minute hands on a clock at these times? Explain or show your reasoning.
3:00
5:00
6:00
How many degrees has the hour hand moved between 3:00 and 7:00? Explain or show how you know.
Problem 6 (Lesson 14)
When Jada looked up at the clock, the long hand pointed at 12. Less than an hour later, she looked up again, and the long hand of the clock had turned 210 degrees. How many minutes had passed? Explain or show your reasoning.
Problem 7 (Lesson 15)
Find the measure of each labeled angle in the drawing. Assume that:
The angles of the triangles meeting at the point in the middle of the figure are all the same.
The other angles of the triangles all have the same measure.
Problem 8 (Lesson 15)
In this diagram each angle on the left hand side is the same as the corresponding angle on the right hand side. Find the measure of angles
Problem 9 (Exploration)
Tyler wonders if the hour hand and minute hand ever point in the same direction at the same time. Can you find some times when the hour hand and minute hand point in the same direction? Explain or show your reasoning.
Problem 10 (Exploration)
Draw a rhombus with a
angle. Explain how you know your shape is a rhombus. Draw another rhombus with a
angle. How are your rhombuses the same? How are they different?
Problem 11 (Exploration)
How many degrees does the minute hand turn in each of the following times? Show how you know.
30 seconds
10 seconds
80 minutes
2.5 hours
Problem 12 (Exploration)
Here are diagrams of some pattern blocks. Each shape has some angles.
How many angles do you see inside each shape?
a triangle
a trapezoid
a rhombus
a hexagon
Here are diagrams of each type of blocks arranged around a shared point.
Use what you know about angle measurement to find the sizes of angles
– . Show your reasoning.