Equations in One Variable
This week your student will be learning to visualize, write, and solve equations. They did this work in previous grades with numbers. In grade 6, we often use a letter called a variable to represent a number whose value is unknown. Diagrams can help us make sense of how quantities are related. Here is an example of such a diagram:

Since 3 pieces are labeled with the same variable x, we know that each of the three pieces represent the same number. Some equations that match this diagram are x+x+x=15 and 15=3x.
A solution to an equation is a number used in place of the variable that makes the equation true. In the previous example, the solution is 5. Think about substituting 5 for x in either equation: 5+5+5=15 and 15=3 \boldcdot 5 are both true. We can tell that, for example, 4 is not a solution, because 4+4+4 does not equal 15.
Solving an equation is a process for finding a solution. Your student will learn that an equation like 15=3x can be solved by dividing each side by 3. Notice that if you divide each side by 3, 15 \div 3 = 3x \div 3, you are left with 5=x, the solution to the equation.
Here is a task to try with your student:
Draw a diagram to represent each equation. Then, solve each equation.
2y=11
11=x+2
Solution:

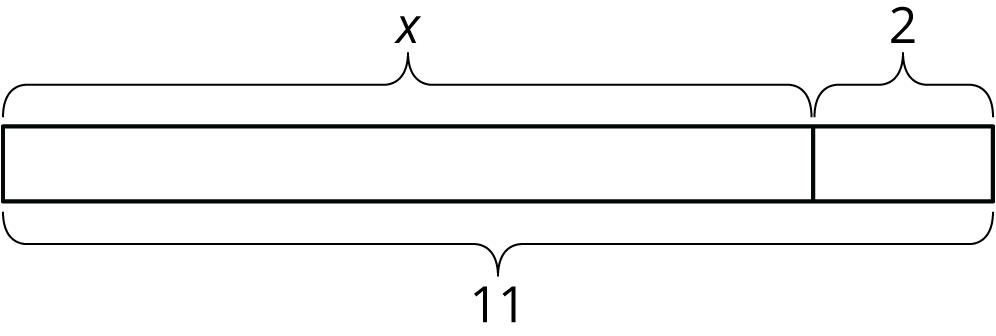
y=5.5 \text{ or }y=\frac{11}{2}
x=9
Equal and Equivalent
This week your student is writing mathematical expressions, especially expressions using the distributive property.

In this diagram, we can say one side length of the large rectangle is 3 units and the other is x + 2 units. So, the area of the large rectangle is 3(x+2). The large rectangle can be partitioned into two smaller rectangles, A and B, with no overlap. The area of A is 6 and the area of B is 3x. So, the area of the large rectangle can also be written as 3x + 6. In other words, 3(x+2)=3x+3\boldcdot2 This is an example of the distributive property.
Here is a task to try with your student:
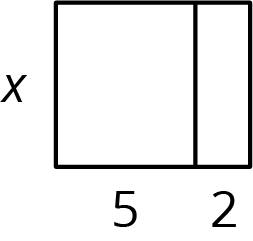
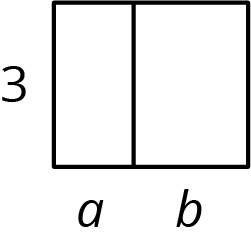
Draw and label a partitioned rectangle to show that each of these equations is always true, no matter the value of the letters.
- 5x+2x=(5+2)x
- 3(a+b)=3a+3b
Solution:
Answers vary. Sample responses:
Expressions with Exponents
This week your student will be working with exponents. When we write an expression like 7^n, we call n the exponent. In this example, 7 is called the base. The exponent tells you how many factors of the base to multiply. For example, 7^4 is equal to 7 \boldcdot 7 \boldcdot 7 \boldcdot 7. In grade 6, students write expressions with whole-number exponents and bases that are
- whole numbers like 7^4
- fractions like \left(\frac17\right) ^ 4
- decimals like 7.7^4
- variables like x^4
Here is a task to try with your student:
Remember that a solution to an equation is a number that makes the equation true. For example, a solution to x^5=30+x is 2, since 2^5=30+2. On the other hand, 1 is not a solution, since 1^5 does not equal 30+1. Find the solution to each equation from the list provided.
- n^2=49
- 4^n=64
- 4^n=4
- \left(\frac{3}{4}\right)^2=n
- 0.2^3=n
- n^4=\frac{1}{16}
- 1^n=1
- {3^n} \div {3^2}=3^3
List: 0, 0.008, \frac12, \frac{9}{16}, \frac{6}{8}, 0.8, 1, 2, 3, 4, 5, 6, 7
Solution:
- 7, because 7^2=49. (Note that -7 is also a solution, but in grade 6 students aren’t expected to know about multiplying negative numbers.)
- 3, because 4^3=64
- 1, because 4^1=4
- \frac{9}{16}, because \left(\frac{3}{4}\right)^2 means \left(\frac{3}{4}\right) \boldcdot \left(\frac{3}{4}\right)
- 0.008, because 0.2^3 means (0.2) \boldcdot (0.2) \boldcdot (0.2)
- \frac12, because \left(\frac{1}{2}\right)^4=\frac{1}{16}
- Any number! 1^n=1 is true no matter what number you use in place of n.
- 5, because this can be rewritten {3^n} \div 9=27. What would we have to divide by 9 to get 27? 243, because 27 \boldcdot 9=243. 3^5=243.
Relationships Between Quantities
This week your student will study relationships between two quantities. For example, since a quarter is worth 25ȼ, we can represent the relationship between the number of quarters, n, and their value v in cents like this:
v = 25n
We can also use a table to represent the situation.
| n | v | |
|---|---|---|
| Row 1 | 1 | 25 |
| Row 2 | 2 | 50 |
| Row 3 | 3 | 75 |
Or we can draw a graph to represent the relationship between the two quantities:

Here is a task to try with your student:
A shopper is buying granola bars. The cost of each granola bar is $0.75.
- Write an equation that shows the cost of the granola bars, c, in terms of the number of bars purchased, n.
- Create a graph representing associated values of c and n.
- What are the coordinates of some points on your graph? What do they represent?
Solutions
- c=0.75n. Every granola bar costs $0.75 and the shopper is buying n of them, so the cost is 0.75n.
- Answers vary. One way to create a graph is to label the horizontal axis with "number of bars" with intervals, 0, 1, 2, 3, etc, and label the vertical axis with "total cost in dollars" with intervals 0, 0.25, 0.50, 0.75, etc.
- If the graph is created as described in this solution, the first coordinate is the number of granola bars and the second is the cost in dollars for that number of granola bars. Some points on such a graph are (2,1.50) and (10,7.50)