Negative Numbers and Absolute Value
This week, your student will work with signed numbers, or positive and negative numbers. We often compare signed numbers when talking about temperatures. For example, -30 degrees Fahrenheit is colder than -10 degrees Fahrenheit. We say “-30 is less than -10” and write: $\text- 30 < \text- 10$.
We also use signed numbers when referring to elevation, or height relative to the sea level. An elevation of 2 feet (which means 2 feet above sea level) is higher than an elevation of -4 feet (which means 4 feet below sea level). We say “2 is greater than -4” and write $2 > \text- 4$.
We can plot positive and negative numbers on the number line. Numbers to the left are always less than numbers to the right.

We can see that -1.3 is less than 0.8 because -1.3 is to the left of 0.8, but -1.3 is greater than -2.7 because it is to the right of -2.7.
We can also talk about a number in terms of its absolute value, or its distance from zero on the number line. For example, 0.8 is 0.8 units away from zero, which we can write as $|0.8| = 0.8$, and -2.7 is 2.7 units away from zero, which we can write as $|\text- 2.7| = 2.7$. The numbers -3 and 3 are both 3 units from 0, which we can write as $|3| = 3$ and $|\text{-}3| = 3$.
Here is a task to try with your student:
-
A diver is at the surface of the ocean, getting ready to make a dive. What is the diver’s elevation in relation to sea level?
-
The diver descends 100 feet to the top of a wrecked ship. What is the diver’s elevation now?
-
The diver descends 25 feet more toward the ocean floor. What is the absolute value of the diver’s elevation now?
-
Plot each of the three elevations as a point on a number line. Label each point with its numeric value.
Solution:
- 0, because sea level is 0 feet above or below sea level
- -100, because the diver is 100 feet below sea level
- The new elevation is -125 feet or 125 feet below sea level, so its absolute value is 125 feet.
- A number line with 0, -100, and -125 marked, as shown:
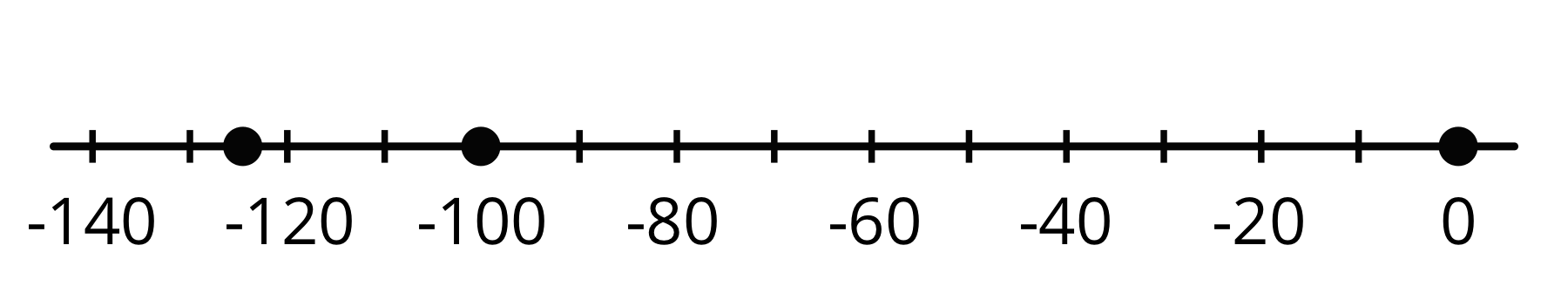
Inequalities
This week, your student will compare positive and negative numbers with inequalities symbols (< and >). They will also graph inequalities in one variable, such as $x < 1$ or $1 > x$, on the number line.
For example, to represent the statement “the temperature in Celsius ($x$) is less than 1 degree,” we can write the inequality $x < 1$ and draw a number line like this:

The diagram shows all numbers to the left of 1 (or less than 1) being possible values of $x$.
We call any value of $x$ that makes an inequality true a solution to the inequality.
This means $x$ values that are greater than -8 are solutions to the inequality $x>\text{-}8$. Likewise, $x$ values that are less than 15 could be a solution to the inequality $x<15$. Depending on the context, however, the solutions may include only positive whole numbers (for example, if $x$ represents the number of students in a class), or any positive and negative numbers, not limited to whole numbers (for example, if $x$ represents temperatures).
Here is a task to try with your student:
A sign at a fair says, “You must be taller than 32 inches to ride the ferris wheel.” Write and graph an inequality that shows the heights of people who are tall enough to ride the ferris wheel.
Solution:
If $x$ represents the height of a person in inches, then the inequality $x >32$ represents the heights of people who can ride the ferris wheel. We can also write the inequality $32 < x$.
The graph of the inequality is:
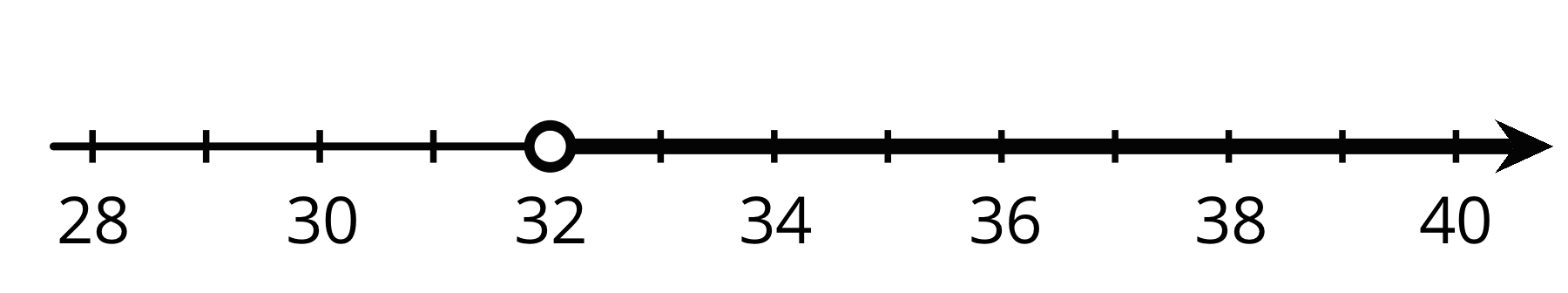
The Coordinate Plane
This week, your student will plot and interpret points on the coordinate plane. In earlier grades, they plotted points where both coordinates are positive, such as point $A$ in the figure. They will now plot points that have positive and negative coordinates, such as points $B$ and $C$.

To find the distance between two points that share the same horizontal line or the same vertical lines, we can simply count the grid units between them. For example, if we plot the point $(2, \text- 4)$ on the grid above (try it!), we can tell that the point will be 7 units away from point $A = (2, 3)$.
Points on a coordinate plane can also represent situations that involve positive and negative numbers. For instance, the points on this coordinate plane shows the temperature in degrees Celsius every hour before and after noon on a winter day. Times before noon are negative and times after noon are positive.

For example, the point $(5, 10)$ tells us that 5 hours after noon, or 5:00 p.m, the temperature was 10 degrees Celsius.
Here is a task to try with your student:
In the graph of temperatures above:
- What was the temperature at 7 a.m.?
- For which recorded times was it colder than 5 degrees Celsius?
Solution:
- It was -5 degrees Celsius at 7:00 a.m. You can see this at the point $(\text- 5, \text- 5)$.
- It was 5 degrees Celsius right at noon, and for the times recorded before that, it was colder.
Common Factors and Common Multiples
This week, your student will solve problems that involve factors and multiples. Because $2 \boldcdot 6 = 12$, we say that 2 and 6 are factors of 12, and that 12 is a multiple of both 2 and 6. The number 12 has other factors: 1, 3, 4, and 12 itself.
Factors and multiples were studied in earlier grades. The focus here is on common factors and common multiples of two whole numbers. For example, 4 is a factor of 8 and a factor of 20, so 4 is a common factor of 8 and 20. 80 is a multiple of 8 and a multiple of 20, so 80 is a common multiple of those two numbers.
One way to find the common factors of two numbers is to list all of the factors for each number and see which factors they have in common. Sometimes we want to find the greatest common factor. To find the greatest common factor of 18 and 24, we first list all the factors of each number and look for the greatest one they have in common.
-
Factors of 18: 1, 2, 3, 6, 9,18
-
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors are 1, 2, 3, and 6. Of these, 6 is the greatest one, so 6 is the greatest common factor of 18 and 24.
To find the common multiples of two numbers, we can do the same. Sometimes we want to find the least common multiple. Let’s find the least common multiple of 18 and 24.
-
Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, . . .
-
Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, . . .
The first two common multiples are 72 and 144. We can see that 72 is the least common multiple.
Here is a task to try with your student:
A cook is making cheese sandwiches to sell. A loaf of bread can make 10 sandwiches. A package of cheese can make 15 sandwiches. How many loaves of bread and how many packages of cheese should the cook buy so that he can make cheese sandwiches without having any bread or any cheese left over?
Solution:
If he is using up the entire loaf of bread, then the number of sandwiches he can make will be a multiple of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, . . .
If he is using up all of the cheese in each package, then the number of sandwiches he can make will be a multiple of 15: 15, 30, 45, 60, 75, 90, 105, . . .
30, 60, and 90 are some of the common multiples.
- To make 30 sandwiches, he will need 3 loaves of bread ($3 \boldcdot 10 =30$) and 2 packages of cheese ($2 \boldcdot 15 =30$).
- To make 60 sandwiches, he will need 6 loaves of bread and 4 packages of cheese.
- To make 90 sandwiches, he will need 9 loaves of bread and 6 packages of cheese.
There are other solutions as well! If he wants to buy the fewest number of loaves and cheese packages, then the first solution is the least.