Proportional Relationships
This week your student will consider what it means to make a useful graph that represents a situation and use graphs, equations, tables, and descriptions to compare two different situations.
There are many successful ways to set up and add scale to a pair of axes in preparation for making a graph of a situation. Sometimes we choose specific ranges for the axes in order to see specific information. For example, if two large, cylindrical water tanks are being filled at a constant rate, we could show the amount of water in them using a graph like this:
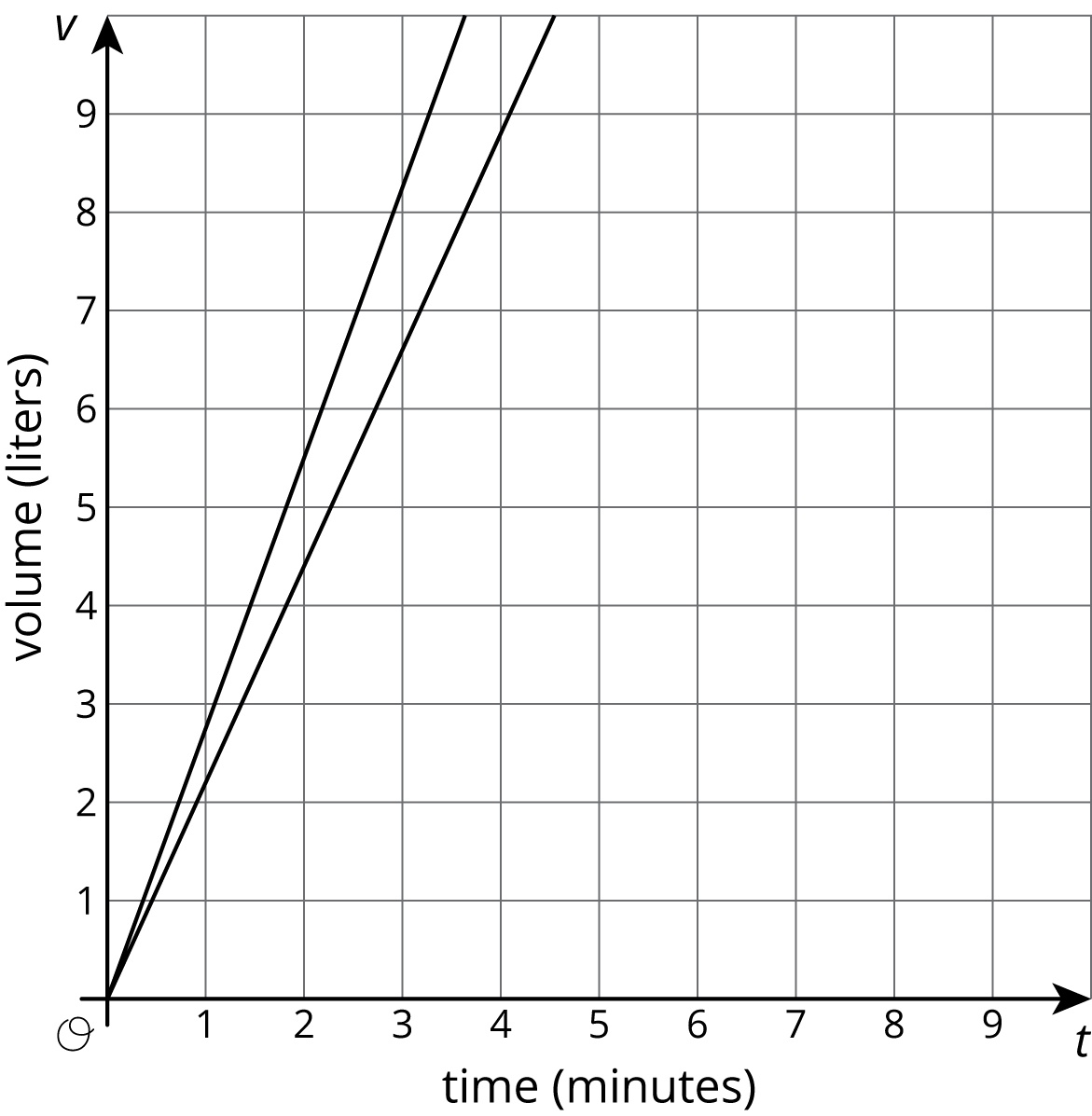
While this graph is accurate, it only shows up to 10 liters, which isn’t that much water. Let’s say we wanted to know how long it would take each tank to have 110 liters. With 110 as a guide, we could set up our axes like this:
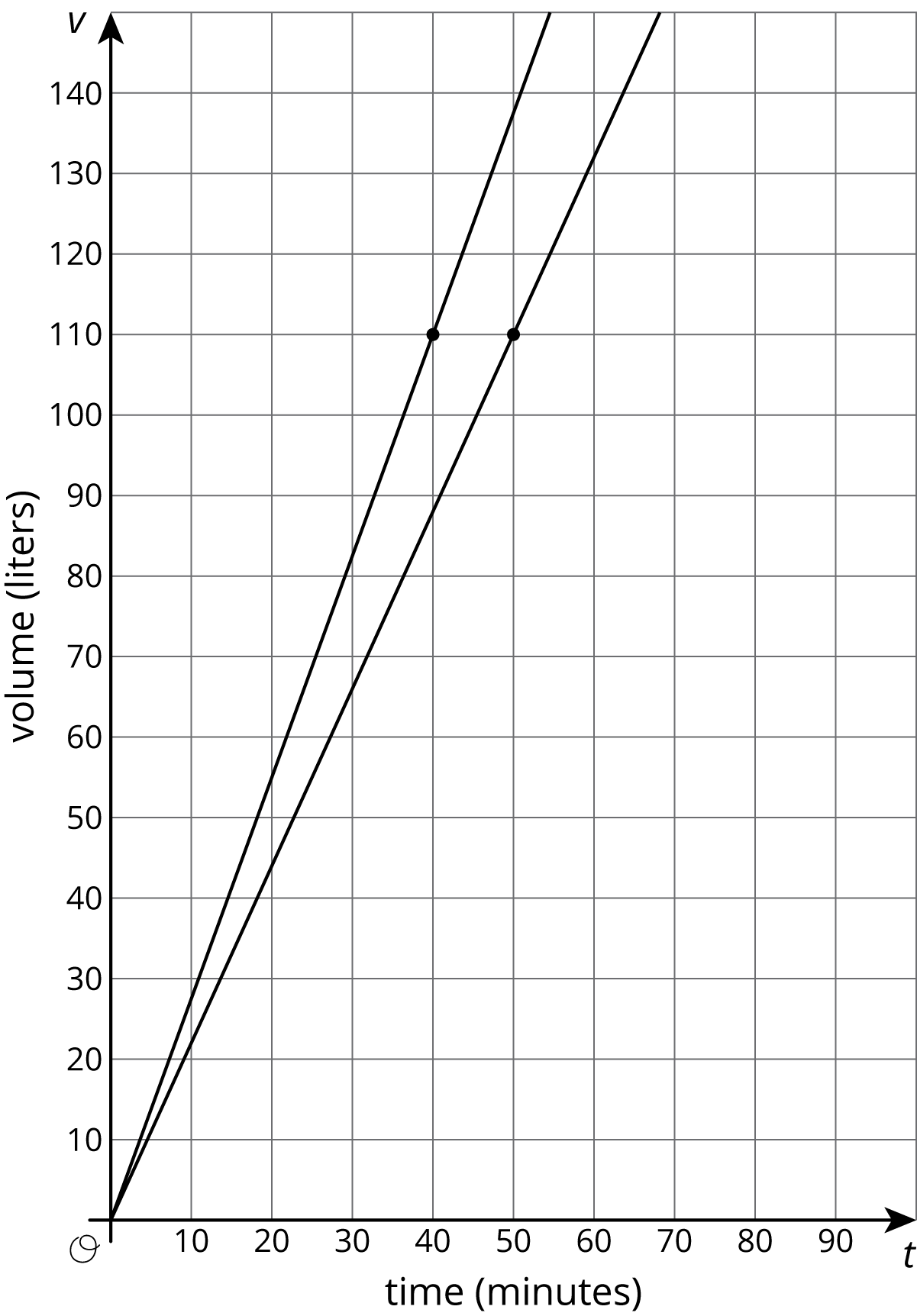
Notice how the vertical scale goes beyond the value we are interested in. Also notice how each axis has values that increase by 10, which, along with numbers like 1, 2, 5, 25, is a friendly number to count by.
Here is a task to try with your student:
This table shows some lengths measured in inches and the equivalent length in centimeters.
| length (inches) | length (centimeters) | |
|---|---|---|
| row 1 | 1 | 2.54 |
| row 2 | 2 | |
| row 3 | 10 | |
| row 4 | 50.8 |
- Complete the table.
- Sketch a graph of the relationships between inches and centimeters. Scale the axis so that all the values in the table can been seen on the graph.
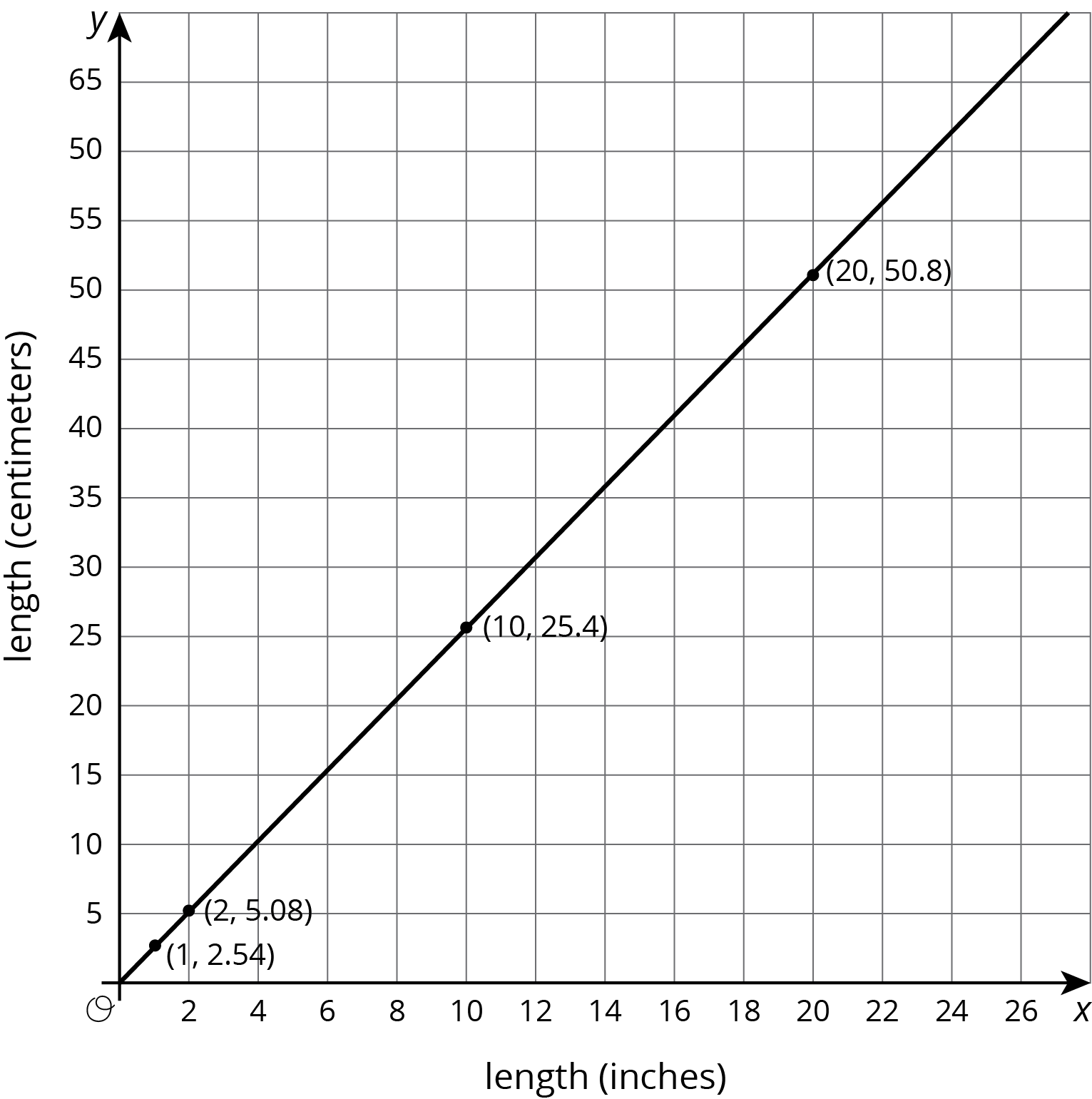
Solution:
-
length (inches) length (centimeters) row 1 1 2.54 row 2 2 5.08 row 3 10 25.4 row 4 20 50.8 -
Representing Linear Relationships
This week your student will learn how to write equations representing linear relationships. A linear relationship exists between two quantities where one quantity has a constant rate of change with respect to the other. The relationship is called linear because its graph is a line.
For example, say we are 5 mile into a hike heading toward a lake at the end of the trail. If we walk at a speed of 2.5 miles per hour, then for each hour that passes we are 2.5 miles further along the trail. After 1 hour we would be 7.5 miles from the start. After 2 hours we would be 10 miles from the start (assuming no stops). This means there is a linear relationship between miles traveled and hours walked. A graph representing this situation is a line with a slope of 2.5 and a vertical intercept of 5.
Here is a task to try with your student:
The graph shows the height in inches, h, of a bamboo plant t months after it has been planted.
- What is the slope of this line? What does that value mean in this context?
- At what point does the line intersect the h-axis? What does that value mean in this context?
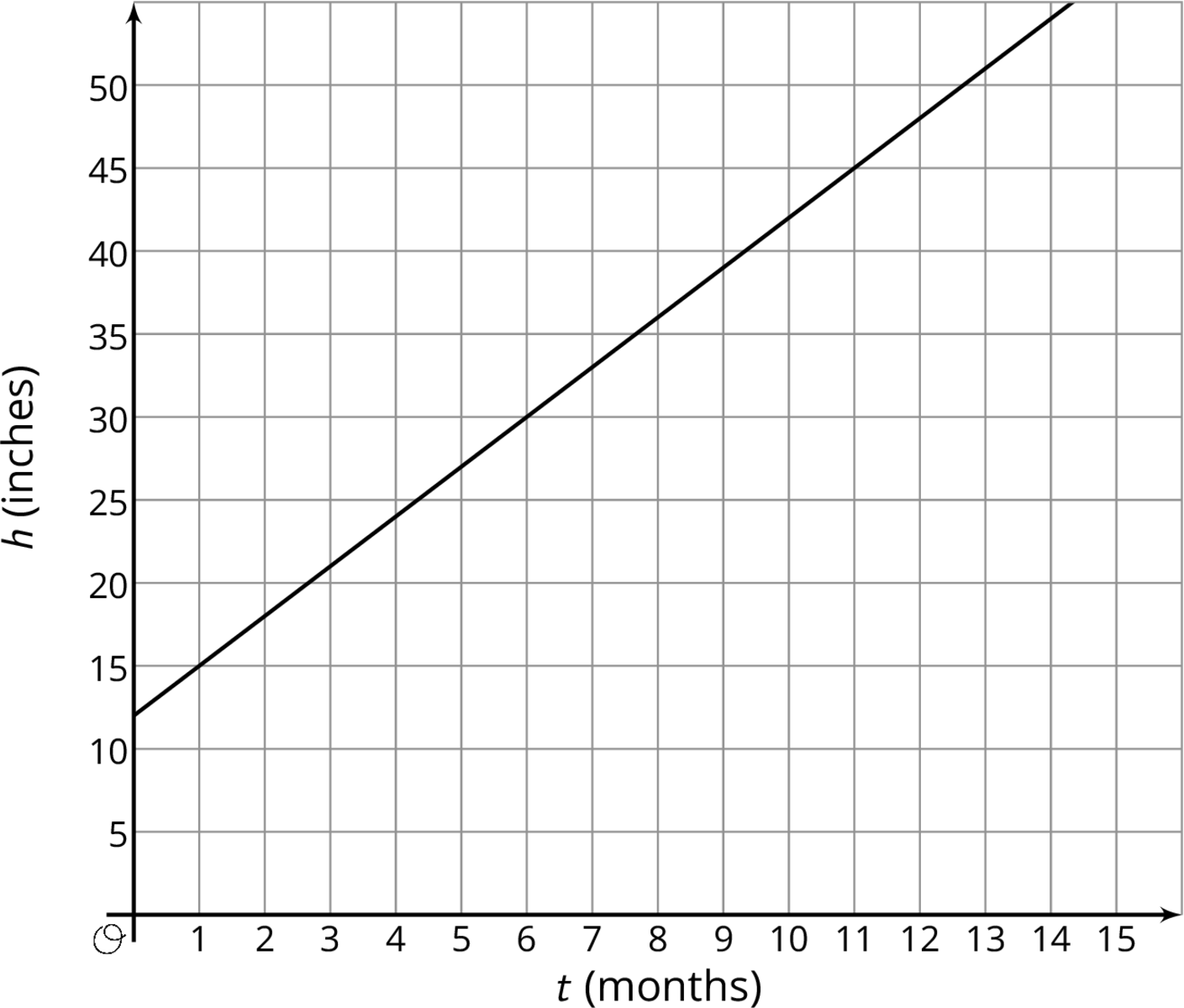
Solution:
- 3. Every month that passes, the bamboo plant grows an additional 3 inches.
- (0,12). This bamboo plant was planted when it was 12 inches tall.
Finding Slopes
This week your student will investigate linear relationships with slopes that are not positive. Here is an example of a line with negative slope that represents the amount of money on a public transit fare card based on the number of rides you take:

The slope of the line graphed here is \text-2.5 since \text{slope}=\frac{\text{vertical change}}{\text{horizontal change}}=\frac{\text-40}{16}=\text-2.5. This corresponds to the cost of 1 ride. The vertical intercept is 40, which means the card started out with $40 on it.
One possible equation for this line is y=\text-2.5x+40. It is important for students to understand that every pair of numbers (x,y) that is a solution to the equation representing the situation is also a point on the graph representing the situation. (We can also say that every point (x,y) on the graph of the situation is a solution to the equation representing the situation.)
Here is a task to try with your student:
A length of ribbon is cut into two pieces. The graph shows the length of the second piece, x, for each length of the first piece, y.

- How long is the original ribbon? Explain how you know.
- What is the slope of the line? What does it represent?
- List three possible pairs of lengths for the two pieces and explain what they mean.
Solution:
- 15 feet. When the second piece is 0 feet long, the first is 15 feet long, so that is the length of the ribbon.
- -1. For each length the second piece increases by, the first piece must decrease by the same length. For example, if we want the second piece to be 1 foot longer, then the first piece must be 1 foot shorter.
- Three possible pairs: (14.5,0.5), which means the second piece is 14.5 feet long so the first piece is only a half foot long. (7.5,7.5), which means each piece is 7.5 feet long, so the original ribbon was cut in half. (0,15), which means the original ribbon was not cut at all to make a second piece, so the first piece is 15 feet long.