Section B: Practice Problems The Size of Angles
Section Summary
Details
In this section, we learned about ways to describe and measure the size of angles.
We used clocks to describe angles as a turn of one away from the other. We learned that a degree is a measure of the turn around a circle and that 1 degree is
Finally, we learned that a protractor is a tool used to measure angles and can also be used to create angles of a certain measure.
A protractor has two sets of numbers and that either set of numbers could be used, but it is helpful to use the set that counts up from 0 rather than count down from 180. We used a protractor to measure and draw different angles.
Problem 1 (Lesson 6)
Write two statements that compare the size of angles A and B.
Draw an angle C that is bigger than both angle A and angle B.
Problem 2 (Lesson 7)
Which set of clock hands make a greater angle? Explain how you know.
Choose one of the clocks and describe how to use the clock to draw the angle represented by the hands on the clock.
Problem 3 (Lesson 8)
This angle has a measure of
How many of these angles can you put together, without overlaps, to make a complete circle? Explain or show how you know.
Explain how you can use the given angle to sketch a
angle.
Problem 4 (Lesson 9)
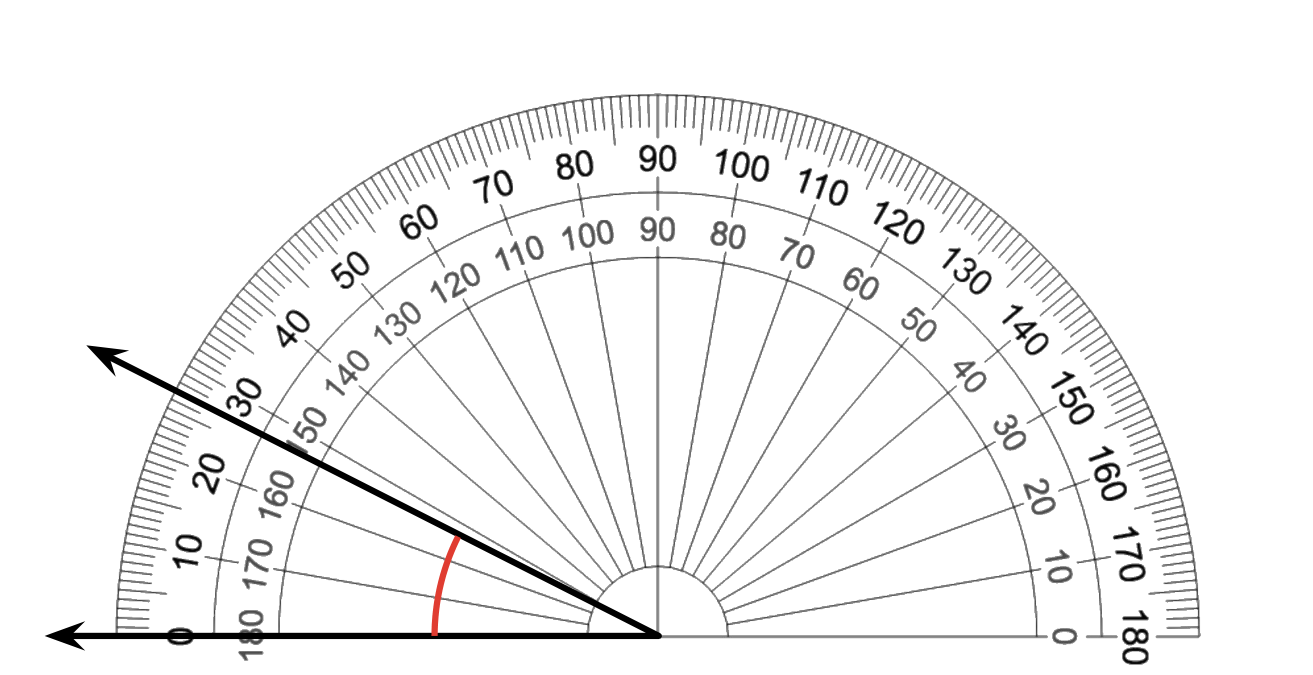
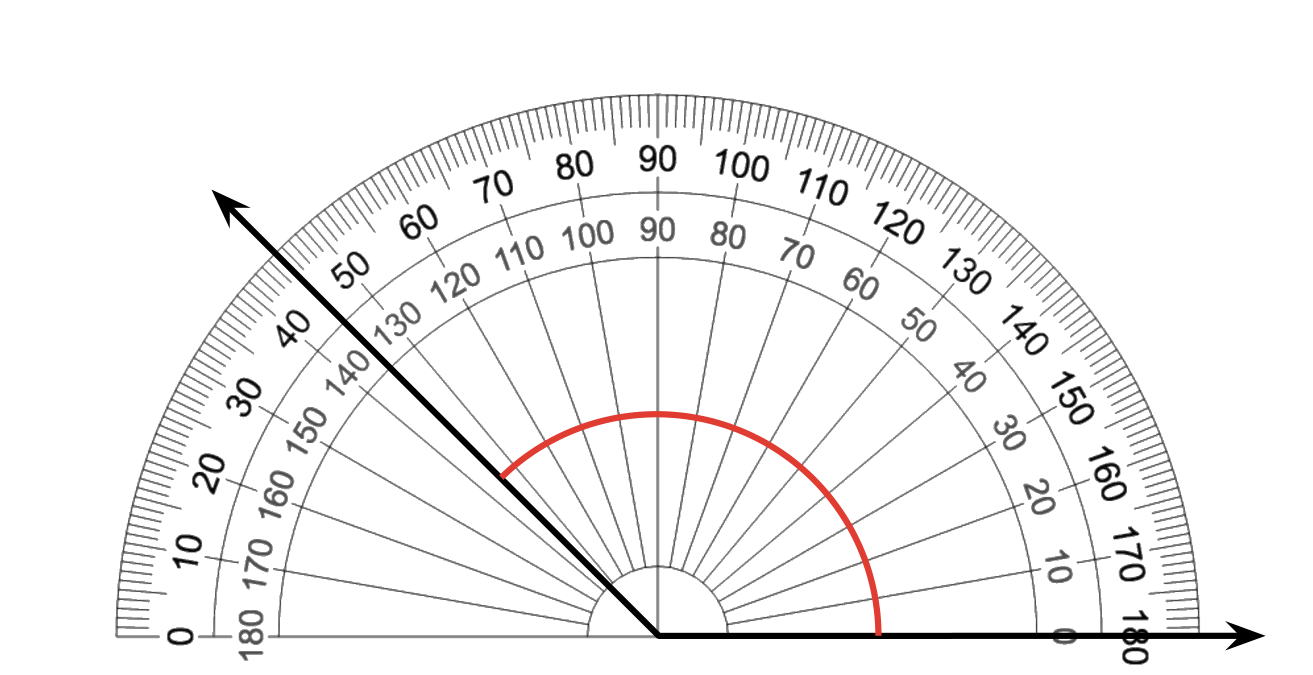
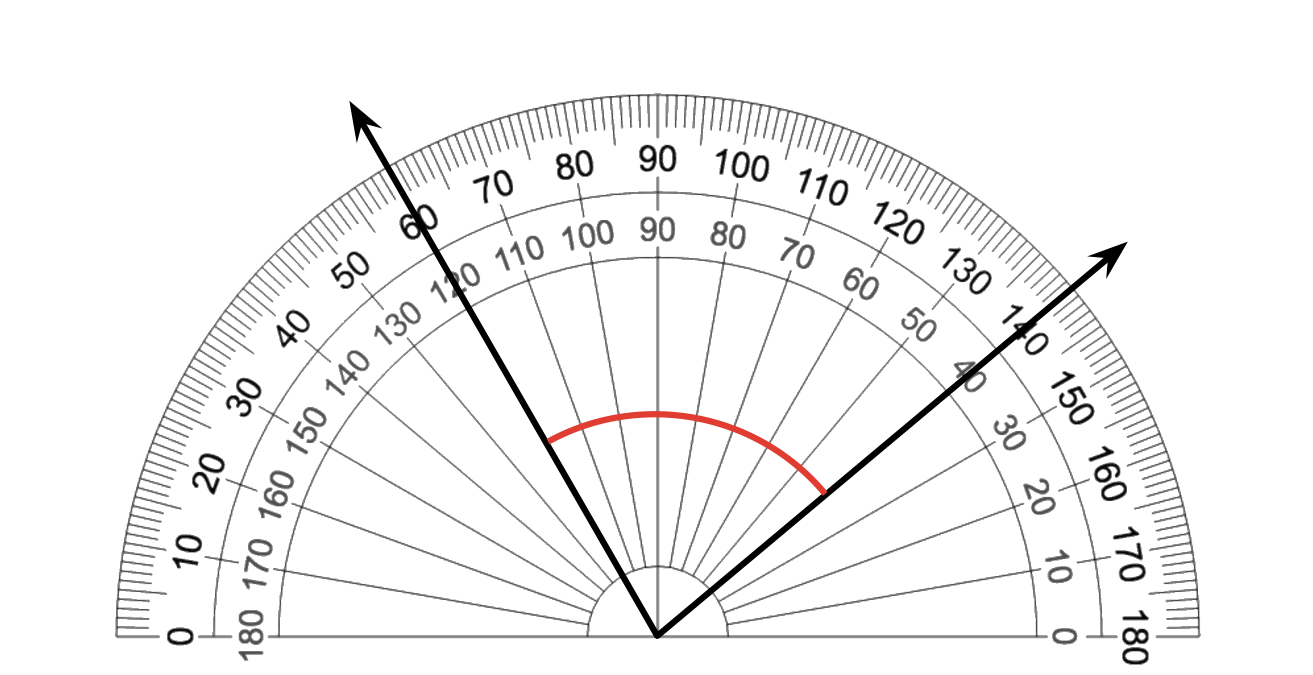
Use the given protractor to find the measurement of each angle.
Problem 5 (Lesson 10)
Which of these shapes have segments that are perpendicular to one another? Trace or circle the perpendicular segments.
Problem 6 (Lesson 11)
Draw a ray. How many different
Problem 7 (Exploration)
What is the smallest angle you can draw?
Can you draw a
angle? What about a
angle or a angle? What is difficult about drawing a small angle?
Problem 8 (Exploration)
What are the measurements of the angles on the pentagon?
Connect every pair of vertices of the pentagon with a line segment. What do you notice? What do you wonder?
Problem 9 (Exploration)
Exploration
Can you estimate or find the measurement of the angle labeled