Lección 4 Exploremos relaciones entre valores posicionales

    • Exploremos relaciones entre valores posicionales.

Calentamiento Observa y pregúntate: Mantén el equilibrio

¿Qué observas? ¿Qué te preguntas?

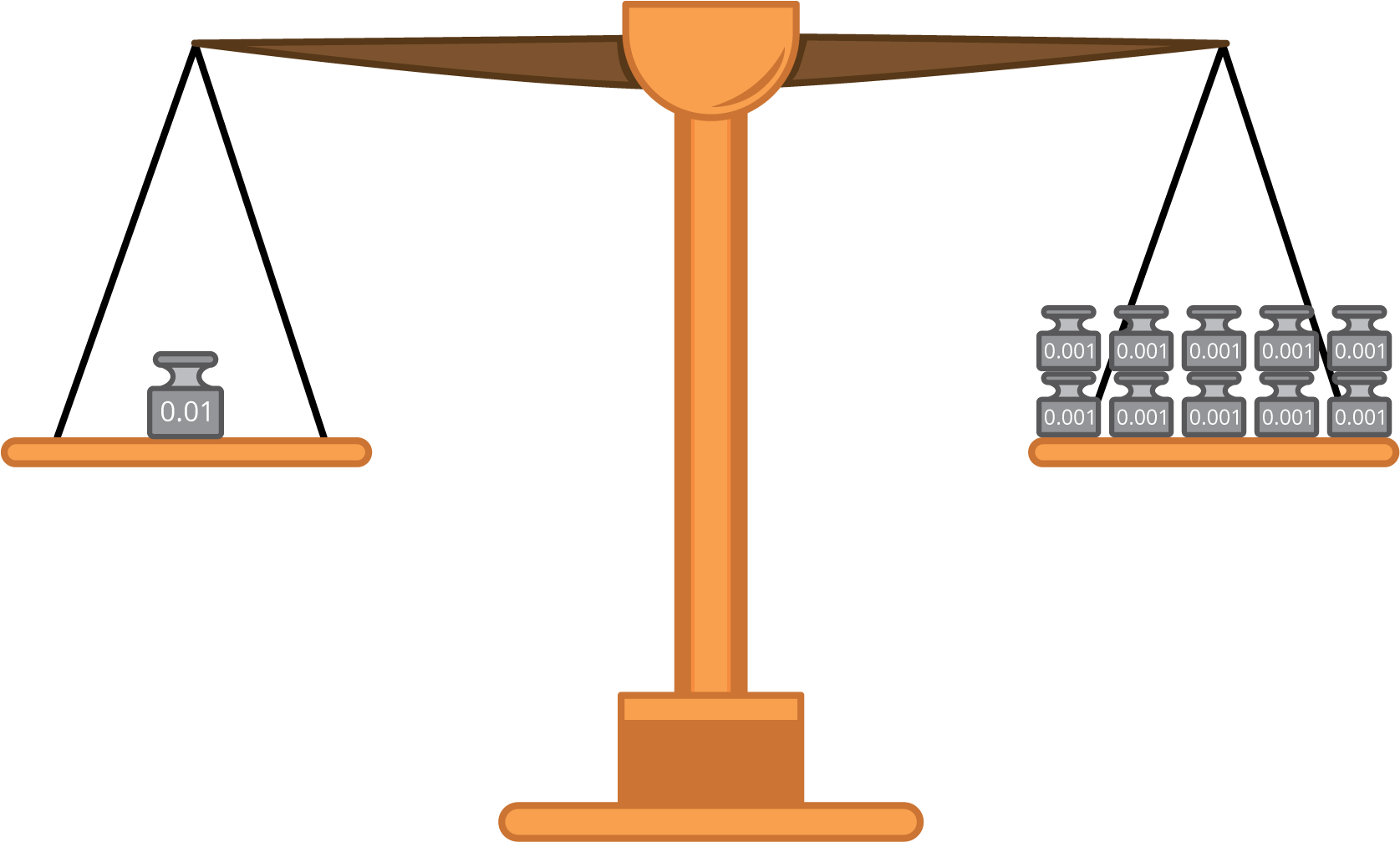
Balanza equilibrada. A la izquierda, 1 peso marcado con 1 centésima. A la derecha, 10 pesos, cada uno marcado con 1 milésima.

Actividad 1 Equilibremos el peso

Problema 1

Balanza inclinada hacia el lado izquierdo. En la placa de la izquierda hay una pepita de oro. En la de la derecha no hay nada.

En cada problema tienes una balanza y pesos de 0.1 onzas, 0.01 onzas y 0.001 onzas.
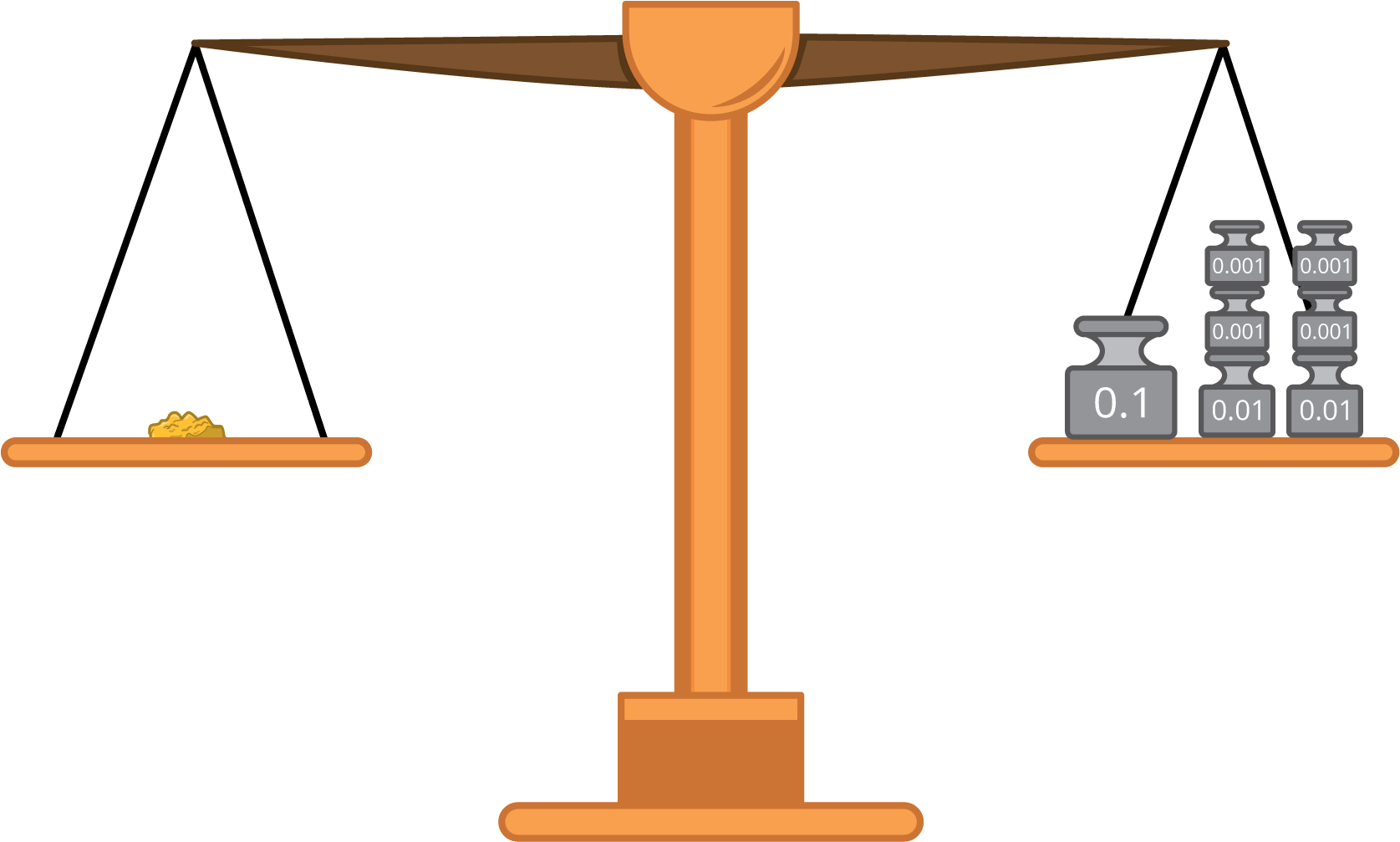
Una pepita de oro pesa 0.2 onzas.

  1. ¿Qué colección de pesos podrías usar para equilibrar la pepita? Explica o muestra tu razonamiento.

  2. ¿Qué otra colección de pesos podrías usar para equilibrar la pepita? Explica o muestra tu razonamiento.

  3. ¿Cuántos pesos de 0.01 onzas necesitarías para equilibrar la pepita?, ¿cuántos pesos de 0.001 onzas?

Problema 2

Otra pepita pesa 0.385 onzas.

  1. ¿Qué colección de pesos podrías usar para equilibrar la pepita? Explica o muestra tu razonamiento.

  2. ¿Cuál es el menor número de pesos que puedes usar para equilibrar la pepita? Explica o muestra tu razonamiento.

  3. ¿Cuál es el mayor número de pesos que puedes usar para equilibrar la pepita? Explica o muestra tu razonamiento.

Problema 3

Escribe un número decimal que represente el peso de las pepitas de oro que se equilibran con:

  1. 266 pesos de 0.001 onzas

  2. 150 pesos de 0.01 onzas

  3. 27 pesos de 0.1 onzas

Actividad 2 Pesos y valores posicionales

Problema 1

Balanza. En la placa de la izquierda hay unas pepitas de oro. En la de la derecha, hay 1 peso de cero punto uno, 2 pesos de cero punto cero uno y 4 pesos de cero punto cero cero uno.

Para equilibrar algunas pepitas de oro se usan varios pesos. Escribe el peso de cada pepita de oro en forma desarrollada.

  1. tres pesos de 0.1 onzas, cinco pesos de 0.01 onzas y ocho pesos de 0.001 onzas

  2. seis pesos de 0.1 onzas y dos pesos de 0.001 onzas

  3. dos pesos de 0.01 onzas y seis pesos de 0.1 onzas

Problema 2

Estos son los pesos, en palabras, de algunas pepitas de oro. Escribe los pesos en forma desarrollada.

  1. doscientas ochenta y tres milésimas de una onza

  2. cuatrocientas nueve milésimas de una onza

Problema 3

Una pepita de oro pesa 0.527 onzas.

  1. ¿Cuál es el valor de cada uno de los dígitos del decimal 0.527?

  2. ¿Cómo se ve el valor de cada dígito del número decimal 0.527 en su forma desarrollada?

Actividad 3 Comparemos valores posicionales usando pesos

Problema 1

  1. ¿Cuántos pesos de 0.01 onzas equilibran un peso de 0.1 onzas? Explica o muestra tu razonamiento.

  2. ¿Cuántos pesos de 0.001 onzas equilibran un peso de 0.1 onzas? Explica o muestra tu razonamiento.

Problema 2

La tabla muestra los pesos de 3 de las pepitas de oro que Diego y sus amigos encontraron lavando oro.

Llena los espacios en blanco. Explica o muestra tu razonamiento.

oro

peso
(gramos)

pepita A

pepita B

pepita C

  1. La pepita A pesa veces lo que pesa la pepita B.

  2. La pepita A pesa veces lo que pesa la pepita C.

  3. La pepita C pesa veces lo que pesa la pepita B.

  4. La pepita C pesa veces lo que pesa la pepita A.

Problema de práctica

Problema 1

  1. Una pepita de oro pesa 0.265 onzas. Escribe 2 colecciones diferentes de pesos de 0.1 onzas, 0.01 onzas y 0.001 onzas que puedas usar para equilibrar la pepita.

    Balanza inclinada hacia la izquierda. En la placa de la izquierda hay una pepita de oro. En la de la derecha no hay nada.

  2. Una primera pepita de oro pesa 0.008 onzas. Una segunda pepita de oro pesa 0.8 onzas.

    • ¿El peso de la segunda pepita es cuántas veces el peso de la primera pepita?

    • ¿El peso de la primera pepita es cuántas veces el peso de la segunda pepita?