2.1: Notice and Wonder: Paper Towels by the Case
Here is a table that shows how many rolls of paper towels a store receives when they order different numbers of cases.
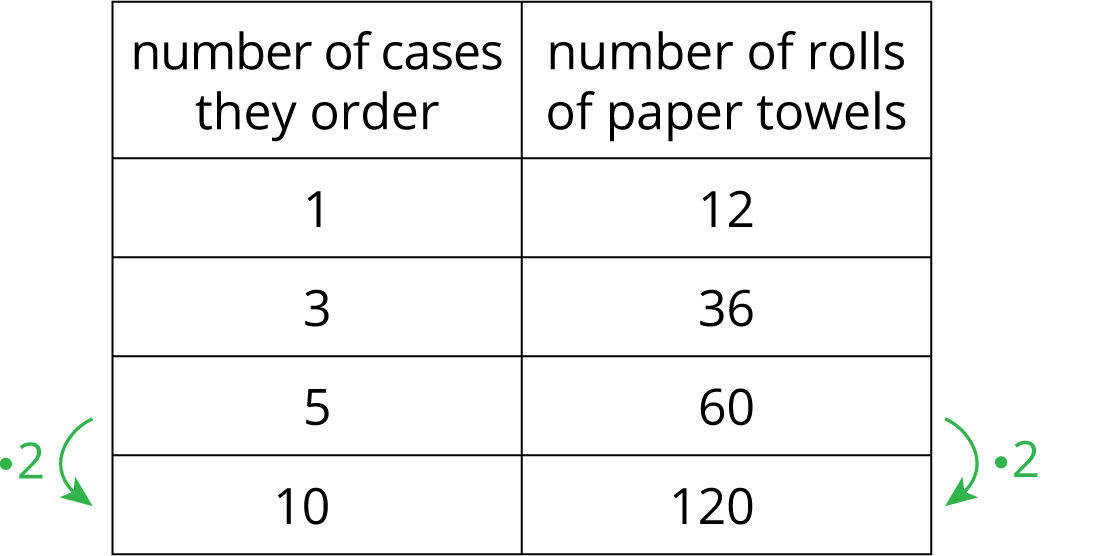
What do you notice about the table? What do you wonder?
Let’s solve problems involving proportional relationships using tables.
Here is a table that shows how many rolls of paper towels a store receives when they order different numbers of cases.

What do you notice about the table? What do you wonder?
A recipe says that 2 cups of dry rice will serve 6 people. Complete the table as you answer the questions. Be prepared to explain your reasoning.
How many people will 10 cups of rice serve?
| row 1 | cups of rice | number of people |
|---|---|---|
| row 2 | 2 | 6 |
| row 3 | 3 | 9 |
| row 4 | 10 | |
| row 5 | 45 |
| row 1 | number of spring rolls | number of people |
|---|---|---|
| row 2 | 6 | 3 |
| row 3 | 30 | |
| row 4 | 40 | |
| row 5 | 28 |
A bakery uses 8 tablespoons of honey for every 10 cups of flour to make bread dough. Some days they bake bigger batches and some days they bake smaller batches, but they always use the same ratio of honey to flour. Complete the table as you answer the questions. Be prepared to explain your reasoning.
How many cups of flour do they use with 20 tablespoons of honey?
How many cups of flour do they use with 13 tablespoons of honey?
How many tablespoons of honey do they use with 20 cups of flour?
| row 1 | honey (tbsp) | flour (c) |
|---|---|---|
| row 2 | 8 | 10 |
| row 3 | 20 | |
| row 4 | 13 | |
| row 5 | 20 |
4 quarters are equal in value to 10 dimes.
| row 1 | number of quarters |
number of dimes |
|---|---|---|
| row 2 | 1 | |
| row 3 | 4 | 10 |
| row 4 | 6 | |
| row 5 | 14 |
If the ratios between two corresponding quantities are always equivalent, the relationship between the quantities is called a proportional relationship.
This table shows different amounts of milk and chocolate syrup. The ingredients in each row, when mixed together, would make a different total amount of chocolate milk, but these mixtures would all taste the same.
Notice that each row in the table shows a ratio of tablespoons of chocolate syrup to cups of milk that is equivalent to 4:1.
About the relationship between these quantities, we could say:
| row 1 | tablespoons of chocolate syrup |
cups of milk |
|---|---|---|
| row 2 | 4 | 1 |
| row 3 | 6 | 1\frac{1}{2} |
| row 4 | 8 | 2 |
| row 5 | \frac{1}{2} | \frac{1}{8} |
| row 6 | 12 | 3 |
| row 7 | 1 | \frac{1}{4} |
We could multiply any value in the chocolate syrup column by \frac14 to get the value in the milk column. We might call \frac14 a unit rate, because \frac14 cups of milk are needed for 1 tablespoon of chocolate syrup. We also say that \frac14 is the constant of proportionality for this relationship. It tells us how many cups of milk we would need to mix with 1 tablespoon of chocolate syrup.
If there is a positive constant k so that the quantities x and y are related by the equation y = kx, then we say that y and x are in a proportional relationship, and that y is proportional to x. The constant k is called the constant of proportionality.
See proportional relationship.