9.1: True or False?
Is each equation true or false? Explain your reasoning.
8=(8+8+8+8)\div3
(10+10+10+10+10)\div5=10
(6+4+6+4+6+4)\div6=5
Let’s look at probabilities of experiments that have multiple steps.
Is each equation true or false? Explain your reasoning.
8=(8+8+8+8)\div3
(10+10+10+10+10)\div5=10
(6+4+6+4+6+4)\div6=5
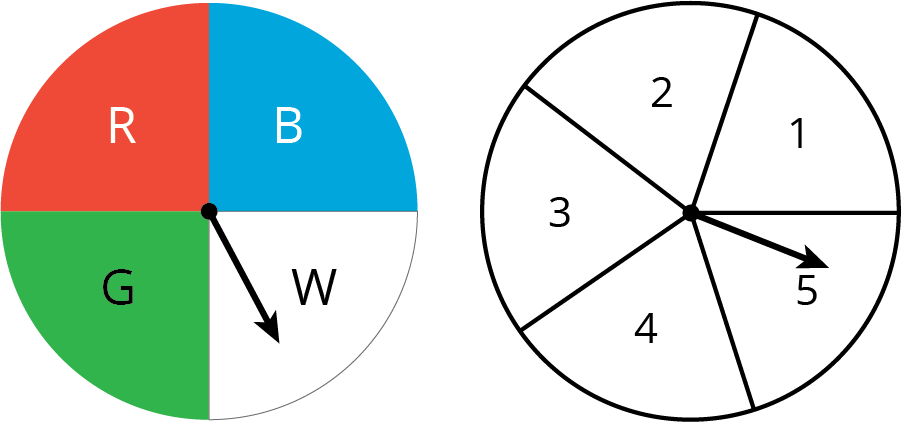
The other day, you wrote the sample space for spinning each of these spinners once.
What is the probability of getting:
The other day you looked at a list, a table, and a tree that showed the sample space for rolling a number cube and flipping a coin.
Your teacher will assign you one of these three structures to use to answer these questions. Be prepared to explain your reasoning.
What is the probability of getting heads and an odd number?
Pause here so your teacher can review your work.
Suppose you roll two number cubes. What is the probability of getting:
Imagine there are 5 cards. They are colored red, yellow, green, white, and black. You mix up the cards and select one of them without looking. Then, without putting that card back, you mix up the remaining cards and select another one.
What is the probability that:
You get a white card and a red card (in either order)?
You get a black card (either time)?
You do not get a black card (either time)?
You get a blue card?
You get 2 cards of the same color?
You get 2 cards of different colors?
In a game using five cards numbered 1, 2, 3, 4, and 5, you take two cards and add the values together. If the sum is 8, you win. Would you rather pick a card and put it back before picking the second card, or keep the card in your hand while you pick the second card? Explain your reasoning.
Suppose we have two bags. One contains 1 star block and 4 moon blocks. The other contains 3 star blocks and 1 moon block.
If we select one block at random from each, what is the probability that we will get two star blocks or two moon blocks?
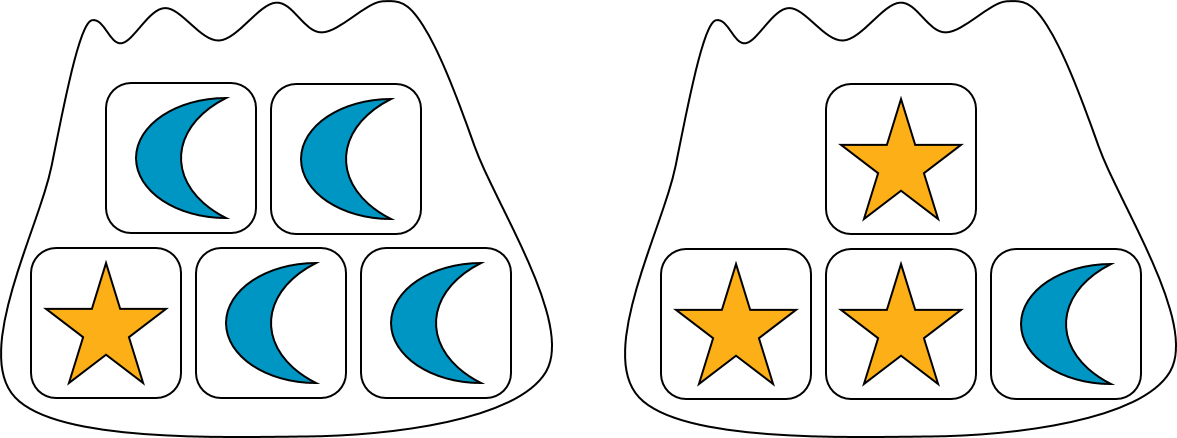
To answer this question, we can draw a tree diagram to see all of the possible outcomes.

There are 5 \boldcdot 4 = 20 possible outcomes. Of these, 3 of them are both stars, and 4 are both moons. So the probability of getting 2 star blocks or 2 moon blocks is \frac{7}{20}.
In general, if all outcomes in an experiment are equally likely, then the probability of an event is the fraction of outcomes in the sample space for which the event occurs.