5.1: Number Talk: Missing Factor
Solve each equation mentally.
16x=176
16x=8
16x=1
\frac15x=1
\frac25x=1
Let’s look at the effects of different scale factors.
Solve each equation mentally.
16x=176
16x=8
16x=1
\frac15x=1
\frac25x=1
Your teacher will give you a set of cards. On each card, Figure A is the original and Figure B is a scaled copy.
Sort the cards based on their scale factors. Be prepared to explain your reasoning.
Examine cards 10 and 13 more closely. What do you notice about the shapes and sizes of the figures? What do you notice about the scale factors?
Examine cards 8 and 12 more closely. What do you notice about the figures? What do you notice about the scale factors?
Triangle B is a scale copy of Triangle A with scale factor \frac12.
Your teacher will give you 2 pieces of a 6-piece puzzle.
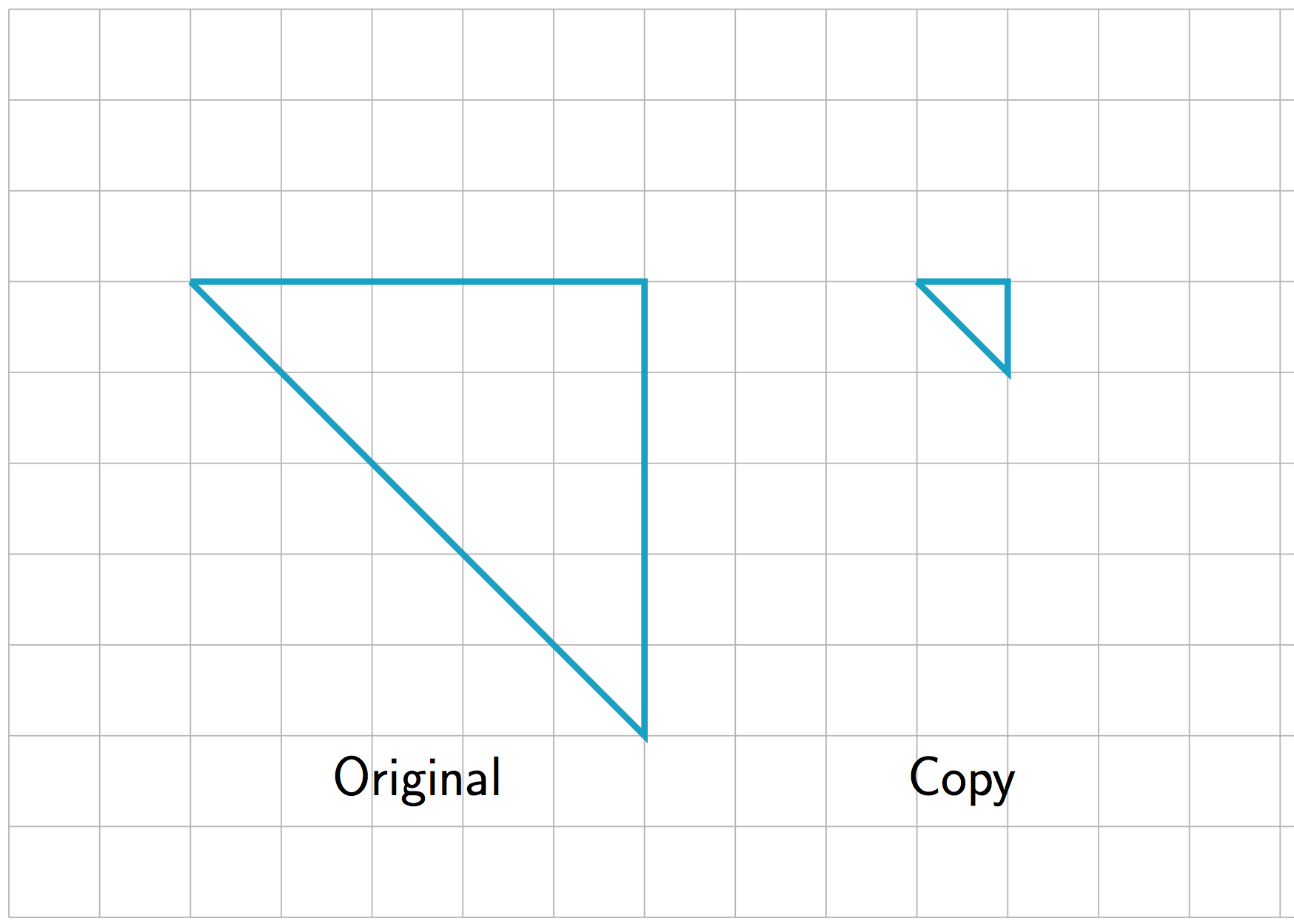
What is the scale factor from the original triangle to its copy? Explain or show your reasoning.
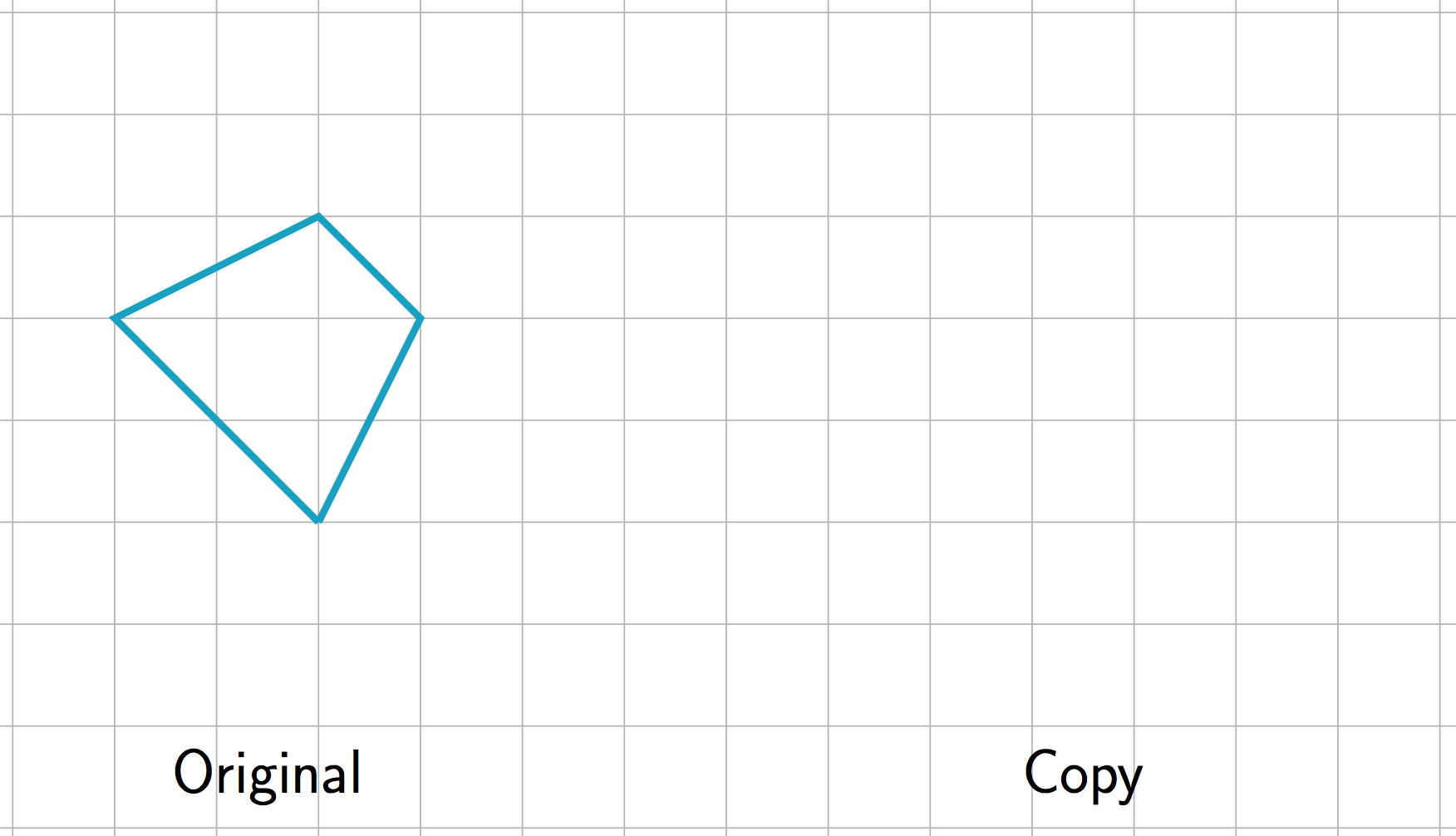
The scale factor from the original trapezoid to its copy is 2. Draw the scaled copy.
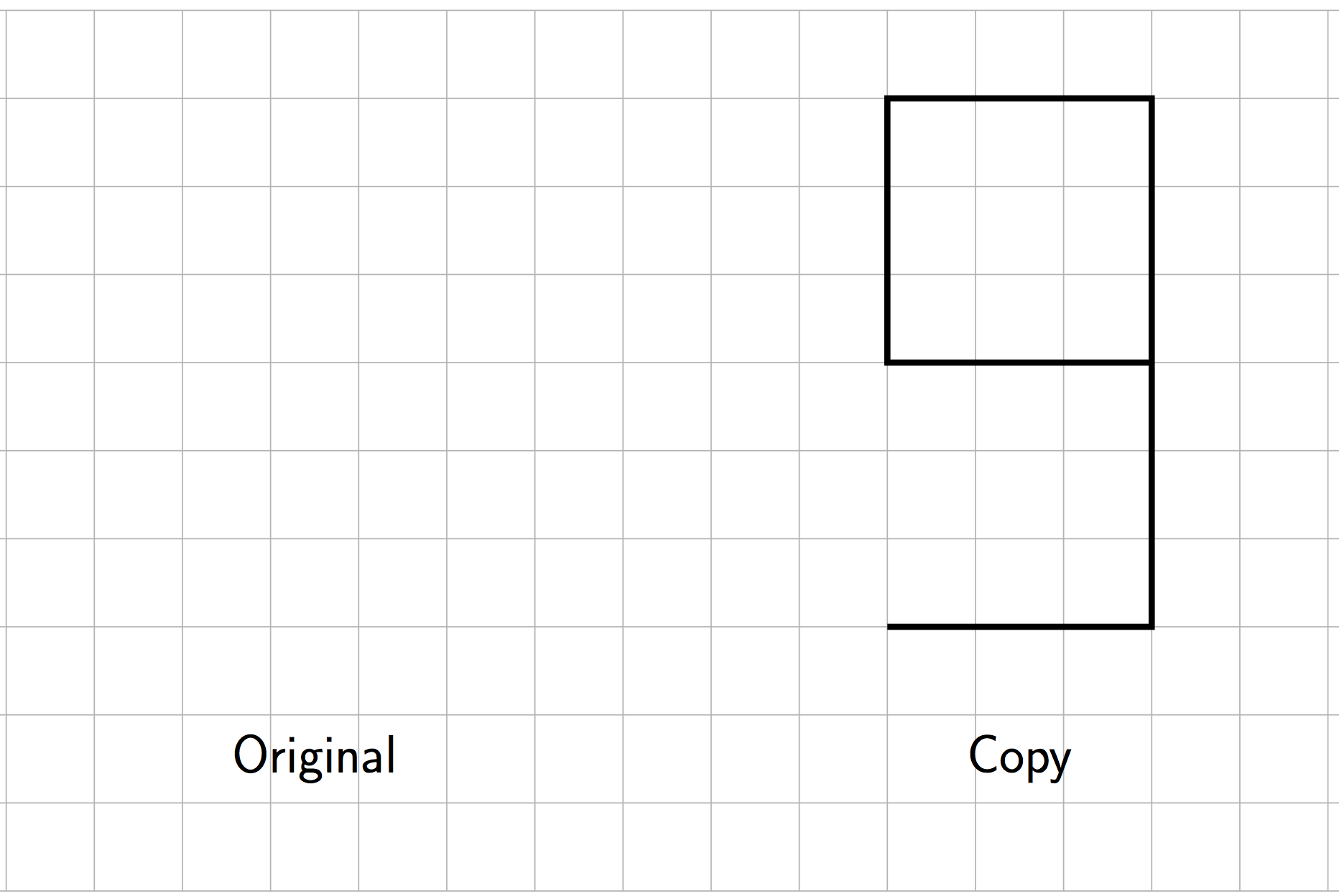


The size of the scale factor affects the size of the copy. When a figure is scaled by a scale factor greater than 1, the copy is larger than the original. When the scale factor is less than 1, the copy is smaller. When the scale factor is exactly 1, the copy is the same size as the original.
Triangle DEF is a larger scaled copy of triangle ABC, because the scale factor from ABC to DEF is \frac32. Triangle ABC is a smaller scaled copy of triangle DEF, because the scale factor from DEF to ABC is \frac23.
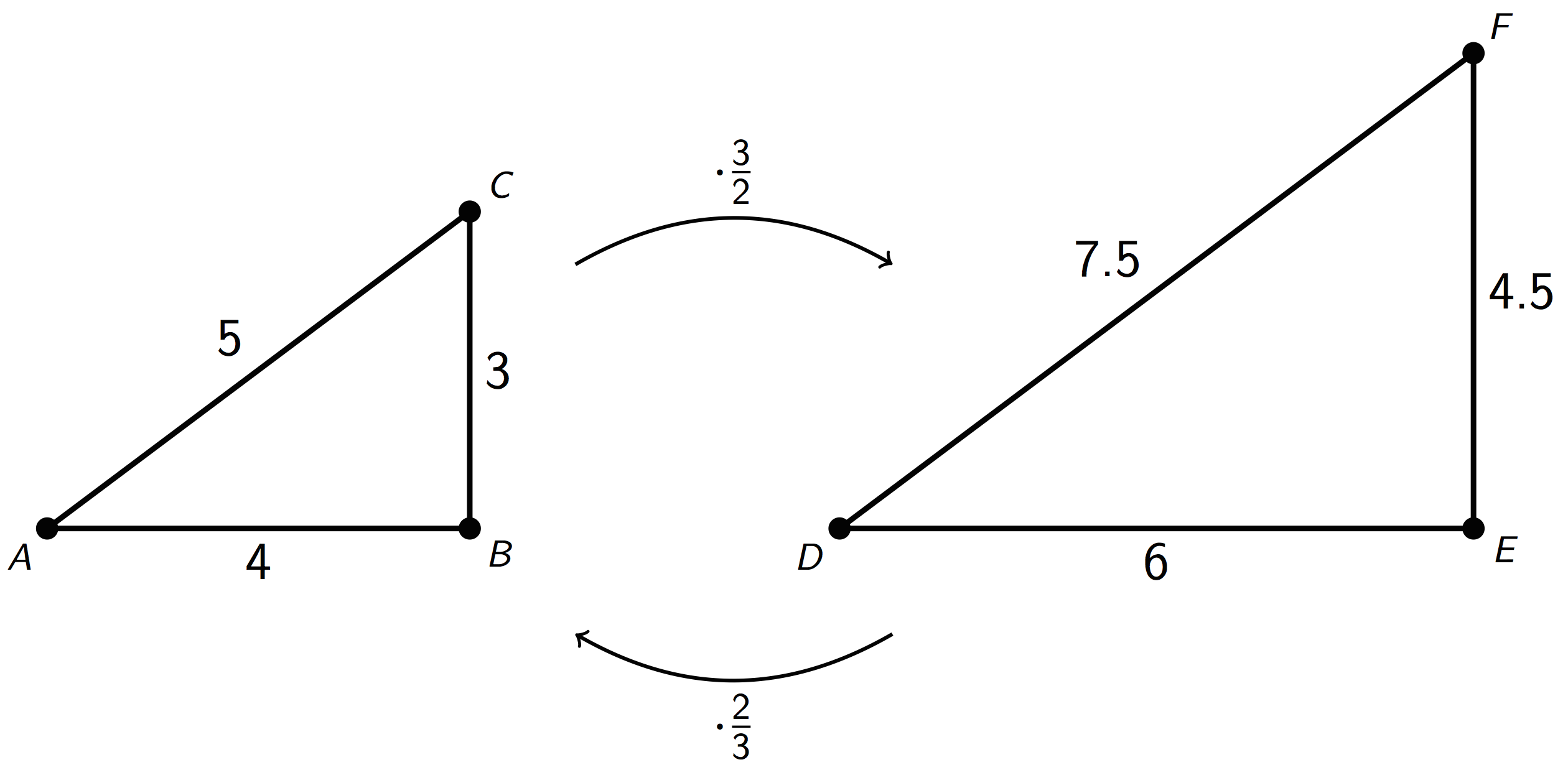
This means that triangles ABC and DEF are scaled copies of each other. It also shows that scaling can be reversed using reciprocal scale factors, such as \frac23 and \frac32.
In other words, if we scale Figure A using a scale factor of 4 to create Figure B, we can scale Figure B using the reciprocal scale factor, \frac14, to create Figure A.