Lesson 2: Changing Temperatures

Let's add signed numbers.

Which pair of arrows doesn't belong?

Complete the table and draw a number line diagram for each situation.

	start ( $^\circ\text{C}$ )	change ( $^\circ\text{C}$ )	final ( $^\circ \text{C}$ )	addition equation
a	+40	10 degrees warmer	+50	$40 + 10 = 50$
b	+40	5 degrees colder
c	+40	30 degrees colder
d	+40	40 degrees colder
e	+40	50 degrees colder

Complete the table and draw a number line diagram for each situation.

	start ( $^\circ\text{C}$ )	change ( $^\circ\text{C}$ )
a	-20	30 degrees warmer
b	-20	35 degrees warmer
c	-20	15 degrees warmer
d	-20	15 degrees colder

Are You Ready For More?

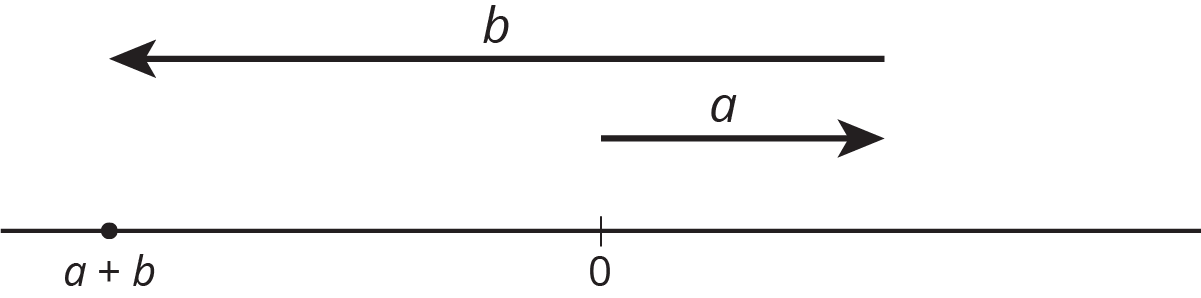
For the numbers $a$ and $b$ represented in the figure, which expression is equal to $|a+b|$ ?

$|a|+|b|$

$|a|-|b|$

$|b|-|a|$

One winter day, the temperature in Houston is 8^\circ Celsius. Find the temperatures in these other cities. Explain or show your reasoning.
1. In Orlando, it is $10^\circ$ warmer than it is in Houston.
2. In Salt Lake City, it is $8^\circ$ colder than it is in Houston.
3. In Minneapolis, it is $20^\circ$ colder than it is in Houston.
In Fairbanks, it is $10^\circ$ colder than it is in Minneapolis. What is the temperature in Fairbanks?
Use the thermometer applet to verify your answers and explore your own scenarios.

GeoGebra Applet WtaGDhSN

Summary

If it is $42^\circ$ outside and the temperature increases by $7^\circ$ , then we can add the initial temperature and the change in temperature to find the final temperature.

$42 + 7 = 49$

If the temperature decreases by $7^\circ$ , we can either subtract $42-7$ to find the final temperature, or we can think of the change as $\text-7^\circ$ . Again, we can add to find the final temperature.

$42 + (\text-7) = 35$

In general, we can represent a change in temperature with a positive number if it increases and a negative number if it decreases. Then we can find the final temperature by adding the initial temperature and the change. If it is $3^\circ$ and the temperature decreases by $7^\circ$ , then we can add to find the final temperature.

$3+ (\text-7) = \text-4$

We can represent signed numbers with arrows on a number line. We can represent positive numbers with arrows that start at 0 and points to the right. For example, this arrow represents +10 because it is 10 units long and it points to the right.
A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the left, and ends at negative 4.There is a solid dot indicated at 4.

We can represent negative numbers with arrows that start at 0 and point to the left. For example, this arrow represents -4 because it is 4 units long and it points to the left.
A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the left, and ends at negative 4.There is a solid dot indicated at 4.

To represent addition, we put the arrows “tip to tail.” So this diagram represents $3+5$ :
A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the right, and ends at 3. A second arrow starts at 3, points to the right, and ends at 8. there is a solid dot indicated at 8.

And this represents $3 + (\text-5)$ :
A number line with the numbers negative 10 through 10 indicated. An arrow starts at 0, points to the right, and ends at three. A second arrow starts at 3, points to the left, and ends at negative 2. There is a solid dot indicated at negative

Lesson 2: Changing Temperatures

2.1: Which One Doesn’t Belong: Arrows

2.2: Warmer and Colder

Are You Ready For More?

2.3: Winter Temperatures

Summary

Practice Problems ▶