2.1: How Do You Figure?
Here are two figures.

Figure C looks more like Figure A than like Figure B. Sketch what Figure C might look like. Explain your reasoning.
Let’s explore circles.
Here are two figures.

Figure C looks more like Figure A than like Figure B. Sketch what Figure C might look like. Explain your reasoning.
Your teacher will give you some pictures of different objects.
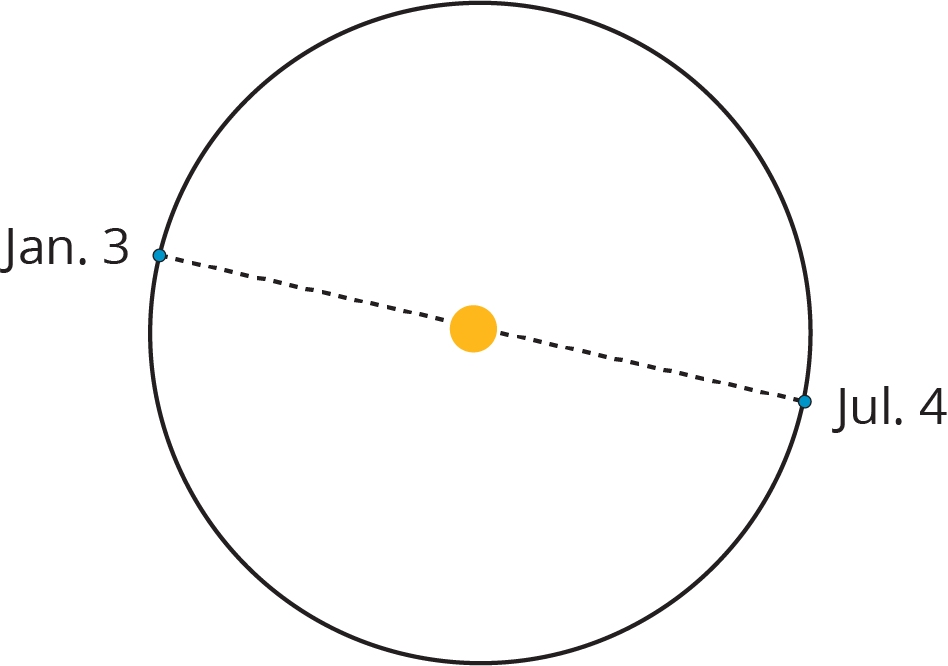
On January 3rd, the Earth is 147,500,000 kilometers away from the Sun. On July 4th, the Earth is 152,500,000 kilometers away from the Sun. The sun has a radius of about 865,000 kilometers.
Could the Earth’s orbit be a circle with some point in the Sun as its center? Explain your reasoning.
Priya, Han, and Mai each measured one of the circular objects from earlier.
Spend some time familiarizing yourself with the tools that are available in this applet.
Draw and label each circle.
A circle consists of all of the points that are the same distance away from a particular point called the center of the circle.
A segment that connects the center with any point on the circle is called a radius. For example, segments QG, QH, QI, and QJ are all radii of circle 2. (We say one radius and two radii.) The length of any radius is always the same for a given circle. For this reason, people also refer to this distance as the radius of the circle.
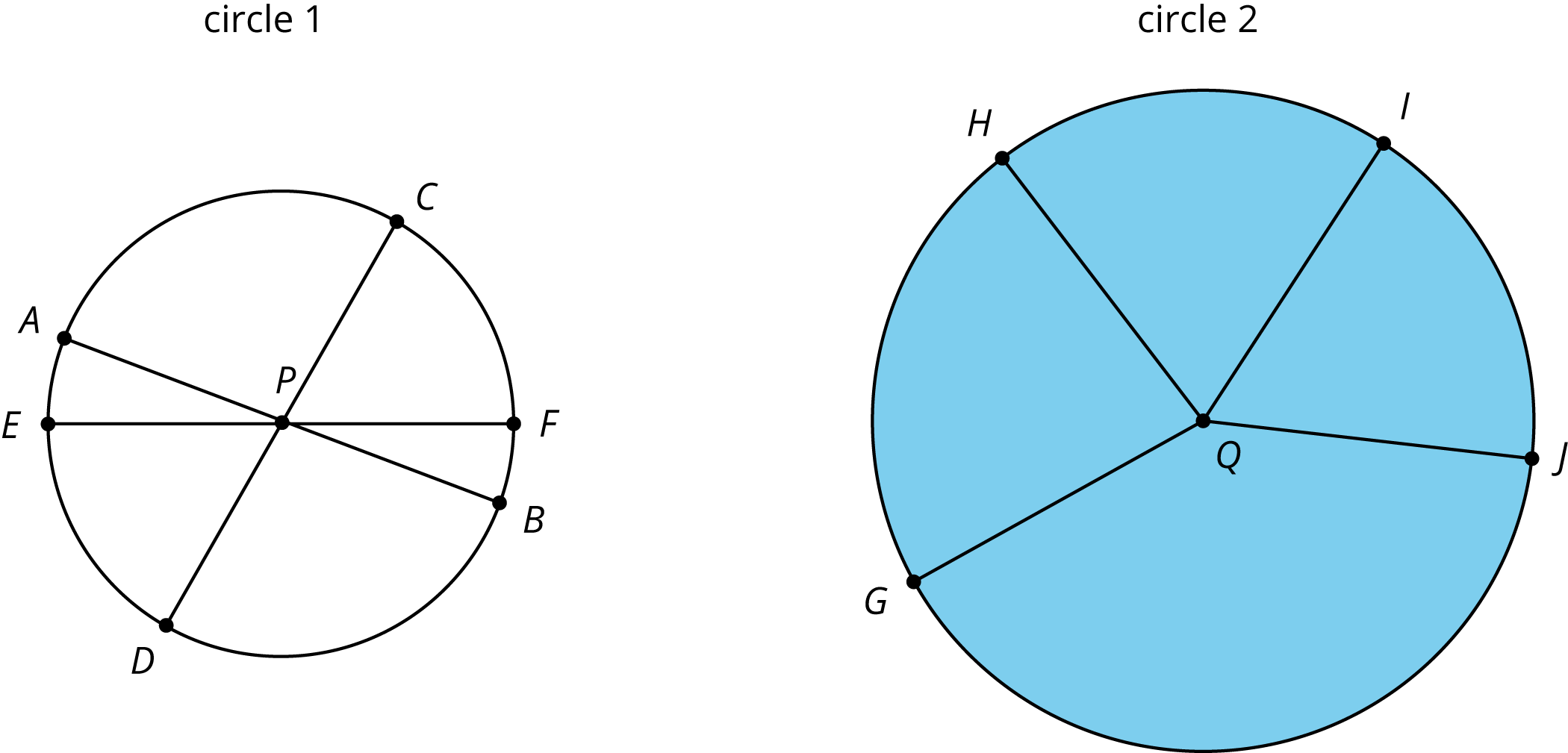
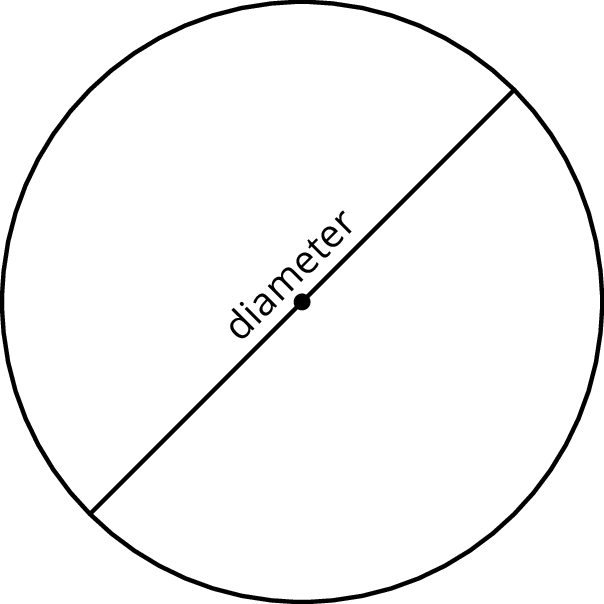
A segment that connects two opposite points on a circle (passing through the circle’s center) is called a diameter. For example, segments AB, CD, and EF are all diameters of circle 1. All diameters in a given circle have the same length because they are composed of two radii. For this reason, people also refer to the length of such a segment as the diameter of the circle.
The circumference of a circle is the distance around it. If a circle was made of a piece of string and we cut it and straightened it out, the circumference would be the length of that string. A circle always encloses a circular region. The region enclosed by circle 2 is shaded, but the region enclosed by circle 1 is not. When we refer to the area of a circle, we mean the area of the enclosed circular region.
The distance from the center of a circle to any point on the circle. Also the corresponding line segment from the center to a point on the circle.
A line segment that has endpoints on a circle and passes through the center is called a diameter of the circle. The length of this segment is also called the diameter.
The circumference of a circle is the distance around the circle. If you imagine the circle as a piece of string, it is the length of the string. If the circle has radius r then the circumference is 2\pi r.
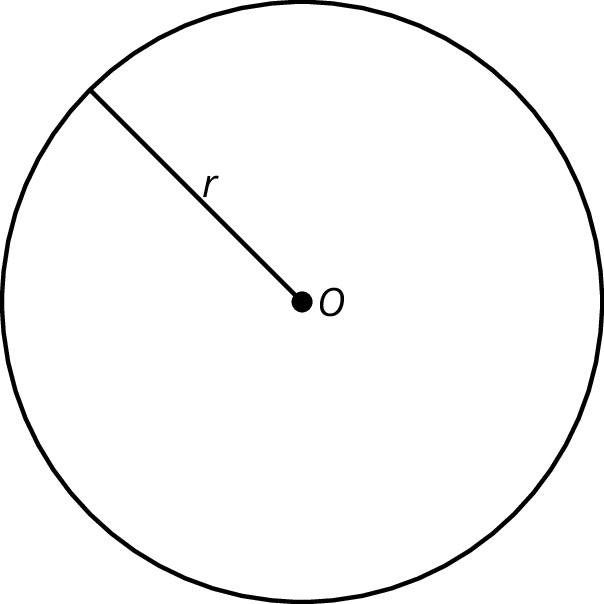
A circle of radius r with center O is the set of all points that are a distance r units from O.
To draw a circle of radius 3 and center O, use a compass to draw all the points at a distance 3 from O.