9.1: Number Talk: What Percentage?
Determine the percentage mentally.
10 is what percentage of 50?
5 is what percentage of 50?
1 is what percentage of 50?
17 is what percentage of 50?
Let’s explore percentages smaller than 1%.
Determine the percentage mentally.
10 is what percentage of 50?
5 is what percentage of 50?
1 is what percentage of 50?
17 is what percentage of 50?
During one waiter’s shift, he delivered appetizers, entrées, and desserts. What percentage of the dishes were desserts? appetizers? entrées? What do your percentages add up to?
Find each percentage of 60. What do you notice about your answers?
30% of 60
3% of 60
0.3% of 60
0.03% of 60
20% of 5,000 is 1,000 and 21% of 5,000 is 1,050. Find each percentage of 5,000 and be prepared to explain your reasoning. If you get stuck, consider using the double number line diagram.
1% of 5,000
0.1% of 5,000
20.1% of 5,000
20.4% of 5,000

15% of 80 is 12 and 16% of 80 is 12.8. Find each percentage of 80 and be prepared to explain your reasoning.
15.1% of 80
15.7% of 80
To make Sierpinski's triangle,

A percentage, such as 30%, is a rate per 100. To find 30% of a quantity, we multiply it by 30\div 100, or 0.3.
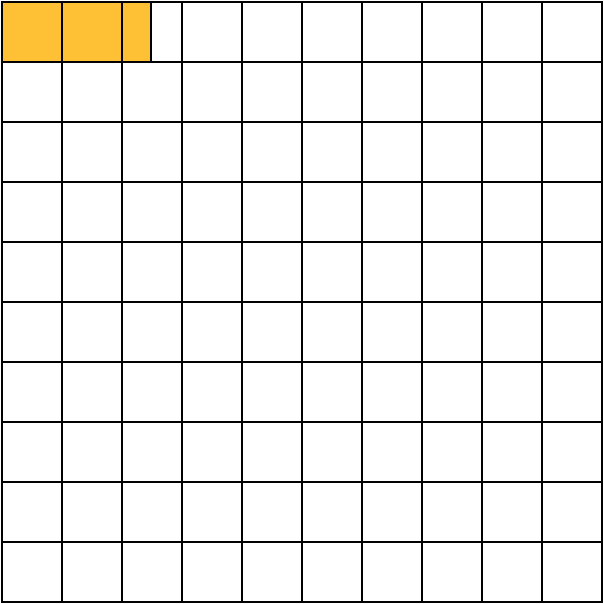 The same method works for percentages that are not whole numbers, like 7.8% or 2.5%. To find 2.5% of a quantity, we multiply it by 2.5 \div 100, or 0.025.
The same method works for percentages that are not whole numbers, like 7.8% or 2.5%. To find 2.5% of a quantity, we multiply it by 2.5 \div 100, or 0.025.
In the square, 2.5% of the area is shaded.
We can sometimes find percentages like 2.5% mentally by using convenient whole number percents. For example, 25% of 80 is one fourth of 80, which is 20. Since 2.5 is one tenth of 25, we know that 2.5% of 80 is one tenth of 20, which is 2.