18.1: Number Talk: Additive Inverses
Find each sum or difference mentally.
\text-30 + \text-10
\text- 10 + \text-30
\text- 30 - 10
10 - \text- 30
Let's find ways to work with subtraction in expressions.
Find each sum or difference mentally.
\text-30 + \text-10
\text- 10 + \text-30
\text- 30 - 10
10 - \text- 30
Lin and Kiran are trying to calculate 7 \frac34 + 3 \frac56 - 1 \frac34. Here is their conversation:
Lin: “I plan to first add 7\frac34 and 3\frac56, so I will have to start by finding equivalent fractions with a common denominator.”
Kiran: “It would be a lot easier if we could start by working with the 1 \frac34 and 7 \frac34. Can we rewrite it like 7 \frac34 + 1 \frac34 - 3 \frac56?”
Lin: “You can’t switch the order of numbers in a subtraction problem like you can with addition; 2-3 is not equal to 3-2.”
Write two expressions for the area of the big rectangle.

Use the distributive property to write an expression that is equivalent to \frac12(8y + \text-x + \text-12). The boxes can help you organize your work.
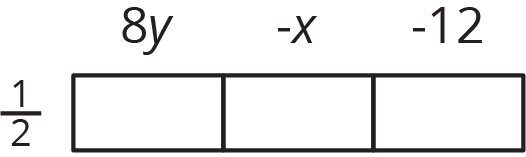
Use the distributive property to write an expression that is equivalent to \frac12(8y - x - 12).
Here is a calendar for April 2017.

Let's choose a date: the 10th. Look at the numbers above, below, and to either side of the 10th: 3, 17, 9, 11.
Working with subtraction and signed numbers can sometimes get tricky. We can apply what we know about the relationship between addition and subtraction—that subtracting a number gives the same result as adding its opposite—to our work with expressions. Then, we can make use of the properties of addition that allow us to add and group in any order. This can make calculations simpler. For example:
\frac58 - \frac23 - \frac18
\frac58 + \text- \frac23 + \text-\frac18
\frac58 + \text-\frac18 + \text- \frac23
\frac48 + \text-\frac23
We can also organize the work of multiplying signed numbers in expressions. The product \frac32(6y-2x-8) can be found by drawing a rectangle with the first factor, \frac32, on one side, and the three terms inside the parentheses on the other side:
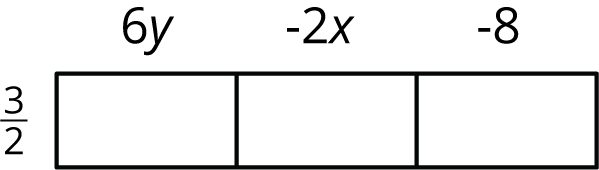
Multiply \frac32 by each term across the top and perform the multiplications:

Reassemble the parts to get the expanded version of the original expression: \frac32(6y-2x-8)=9y-3x-12