Grade 7, Unit 6.15 - Open Up Resources

Here is an inequality: $\text-x \geq \text-4$ .

Predict what you think the solutions on the number line will look like.
Select all the values that are solutions to \text-x \geq \text-4:
1. 3
2. -3
3. 4
4. -4
5. 4.001
6. -4.001
Graph the solutions to the inequality on the number line:

Let's investigate the inequality $x-3>\text-2$ .

$x$ -4 -3 -2 -1 0 1 2 3 4

$x-3$ -7 -5 -1 1
1. Complete the table.
2. For which values of $x$ is it true that $x - 3 = \text-2$ ?
3. For which values of $x$ is it true that $x - 3 > \text-2$ ?
4. Graph the solutions to $x - 3 > \text-2$ on the number line:
Here is an inequality: $2x<6$ .
1. Predict which values of $x$ will make the inequality $2x < 6$ true.
2. Complete the table. Does it match your prediction?
  
  $x$ -4 -3 -2 -1 0 1 2 3 4
  
  $2x$
3. Graph the solutions to $2x < 6$ on the number line:
Here is an inequality: $\text-2x<6$ .
1. Predict which values of $x$ will make the inequality $\text-2x < 6$ true.
2. Complete the table. Does it match your prediction?
  
  $x$ -4 -3 -2 -1 0 1 2 3 4
  
  $\text-2x$
3. Graph the solutions to $\text-2x < 6$ on the number line:
4. How are the solutions to $2x<6$ different from the solutions to $\text-2x<6$ ?

$x$	-4	-3	-2	-1	0	1	2	3	4
$x-3$	-7		-5				-1		1

$x$	-4	-3	-2	-1	0	1	2	3	4
$2x$

$x$	-4	-3	-2	-1	0	1	2	3	4
$\text-2x$

Let’s investigate \text-4x + 5 \geq 25.
1. Solve $\text-4x+5 = 25$ .
2. Is $\text-4x + 5 \geq 25$ true when $x$ is 0? What about when $x$ is 7? What about when $x$ is -7?
3. Graph the solutions to $\text-4x + 5 \geq 25$ on the number line.
Let's investigate \frac{4}{3}x+3 < \frac{23}{3}.
1. Solve $\frac43x+3 = \frac{23}{3}$ .
2. Is $\frac{4}{3}x+3 < \frac{23}{3}$ true when $x$ is 0?
3. Graph the solutions to $\frac{4}{3}x+3 < \frac{23}{3}$ on the number line.
Solve the inequality $3(x+4) > 17.4$ and graph the solutions on the number line.
Solve the inequality $\text-3\left(x-\frac43\right) \leq 6$ and graph the solutions on the number line.

Are You Ready For More?

Write at least three different inequalities whose solution is $x > \text-10$ . Find one with $x$ on the left side that uses a $<$ .

Summary

Here is an inequality: $3(10-2x) < 18$ . The solution to this inequality is all the values you could use in place of $x$ to make the inequality true.

In order to solve this, we can first solve the related equation $3(10-2x) = 18$ to get the solution $x = 2$ . That means 2 is the boundary between values of $x$ that make the inequality true and values that make the inequality false.

To solve the inequality, we can check numbers greater than 2 and less than 2 and see which ones make the inequality true.

Let’s check a number that is greater than 2: $x= 5$ . Replacing $x$ with 5 in the inequality, we get $3(10-2 \boldcdot 5) < 18$ or just $0 < 18$ . This is true, so $x=5$ is a solution. This means that all values greater than 2 make the inequality true. We can write the solutions as $x > 2$ and also represent the solutions on a number line:

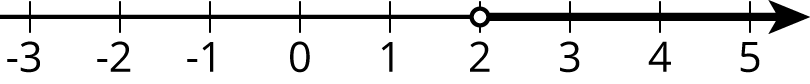
Notice that 2 itself is not a solution because it's the value of $x$ that makes $3(10-2x)$ equal to 18, and so it does not make $3(10-2x) < 18$ true.

For confirmation that we found the correct solution, we can also test a value that is less than 2. If we test $x=0$ , we get $3(10-2 \boldcdot 0) < 18$ or just $30 < 18$ . This is false, so $x = 0$ and all values of $x$ that are less than 2 are not solutions.

Lesson 15: Efficiently Solving Inequalities

15.1: Lots of Negatives

15.2: Inequalities with Tables

15.3: Which Side are the Solutions?

Are You Ready For More?

Summary

Practice Problems ▶