Let’s solve more problems involving proportional relationships using tables.
Use the numbers and units from the list to find as many equivalent measurements as you can. For example, you might write “30 minutes is \frac12 hour.”
You can use the numbers and units more than once.
1
12
0.4
60
50
\frac{1}{2}
40
0.01
3\frac{1}{3}
30
0.3
24
\frac{1}{5}
6
2
centimeter
meter
hour
feet
minute
inch
There is a proportional relationship between any length measured in centimeters and the same length measured in millimeters.
There are two ways of thinking about this proportional relationship.
If you know the length of something in centimeters, you can calculate its length in millimeters.
| row 1 | length (cm) | length (mm) |
|---|---|---|
| row 2 | 9 | |
| row 3 | 12.5 | |
| row 4 | 50 | |
| row 5 | 88.49 |
If you know the length of something in millimeters, you can calculate its length in centimeters.
| row 1 | length (mm) | length (cm) |
|---|---|---|
| row 2 | 70 | |
| row 3 | 245 | |
| row 4 | 4 | |
| row 5 | 699.1 |
Complete each sentence:
On its way from New York to San Diego, a plane flew over Pittsburgh, Saint Louis, Albuquerque, and Phoenix traveling at a constant speed.
Complete the table as you answer the questions. Be prepared to explain your reasoning.
Map of the path of a plane flying from Pittsburgh to Phoenix
Copyright Owner:
American Fact Finder
License:
Public Domain
Via:
American Fact Finder
| segment | time | distance | speed |
|---|---|---|---|
| Pittsburgh to Saint Louis | 1 hour | 550 miles | |
| Saint Louis to Albuquerque | 1 hour 42 minutes | ||
| Albuquerque to Phoenix | 330 miles |
What is the distance between Saint Louis and Albuquerque?
How many minutes did it take to fly between Albuquerque and Phoenix?
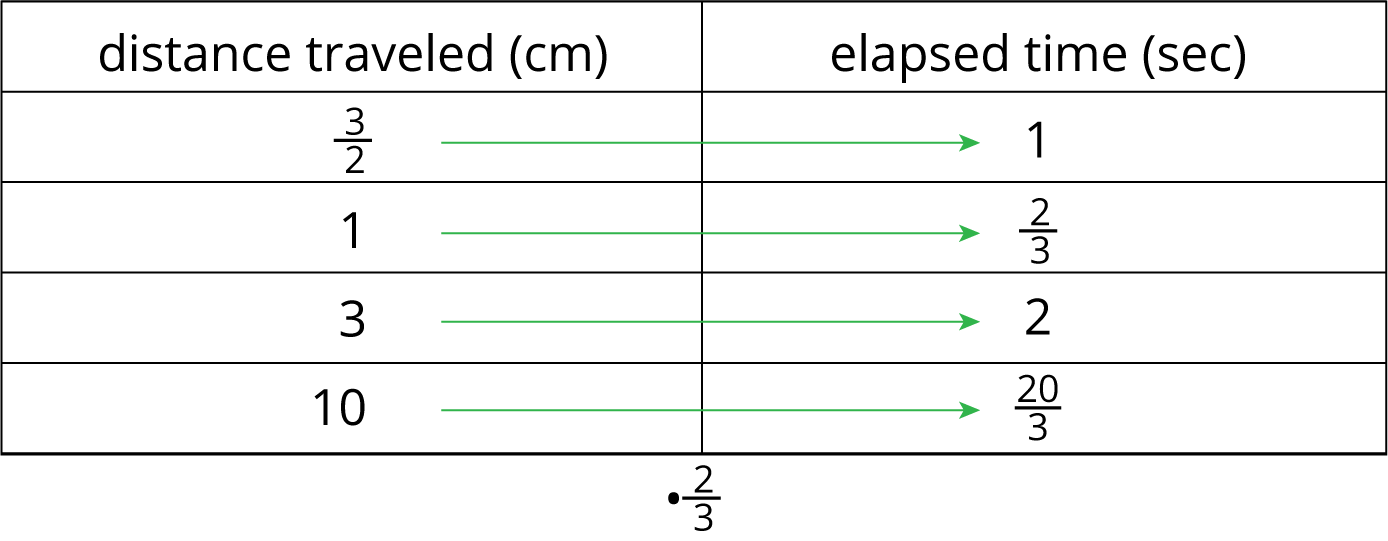
When something is traveling at a constant speed, there is a proportional relationship between the time it takes and the distance traveled. The table shows the distance traveled and elapsed time for a bug crawling on a sidewalk.
We can multiply any number in the first column by \frac23 to get the corresponding number in the second column. We can say that the elapsed time is proportional to the distance traveled, and the constant of proportionality is \frac23. This means that the bug’s pace is \frac23 seconds per centimeter.
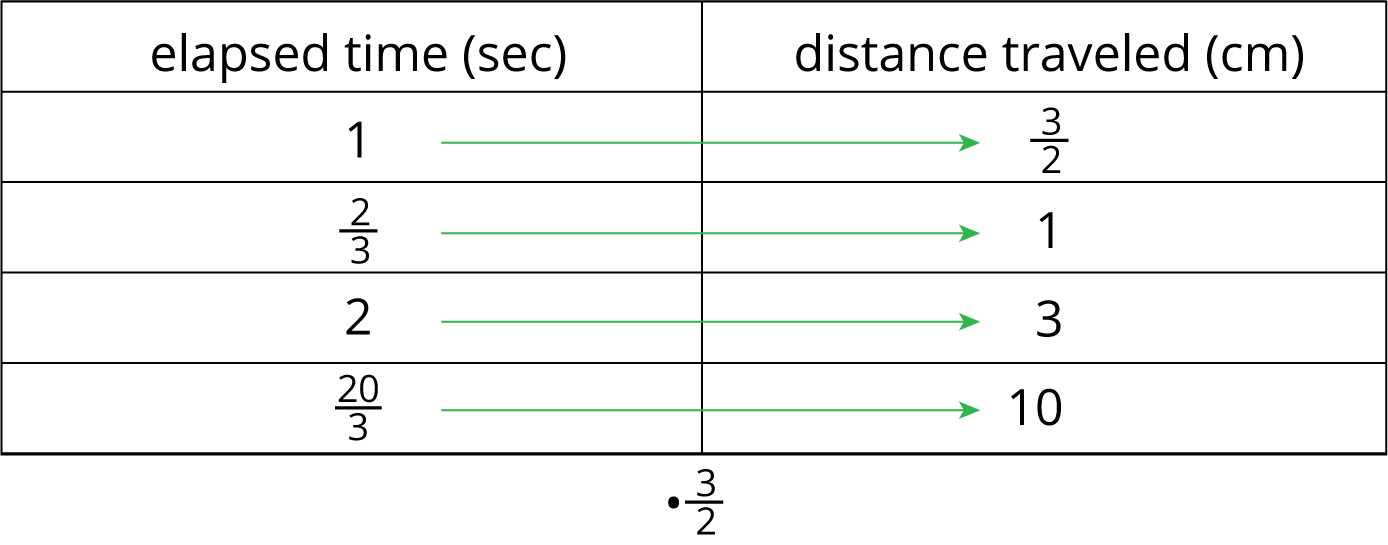
This table represents the same situation, except the columns are switched.
We can multiply any number in the first column by \frac32 to get the corresponding number in the second column. We can say that the distanced traveled is proportional to the elapsed time, and the constant of proportionality is \frac32. This means that the bug’s speed is \frac32 centimeters per second.
Notice that \frac32 is the reciprocal of \frac23. When two quantities are in a proportional relationship, there are two constants of proportionality, and they are always reciprocals of each other. When we represent a proportional relationship with a table, we say the quantity in the second column is proportional to the quantity in the first column, and the corresponding constant of proportionality is the number we multiply values in the first column to get the values in the second.
