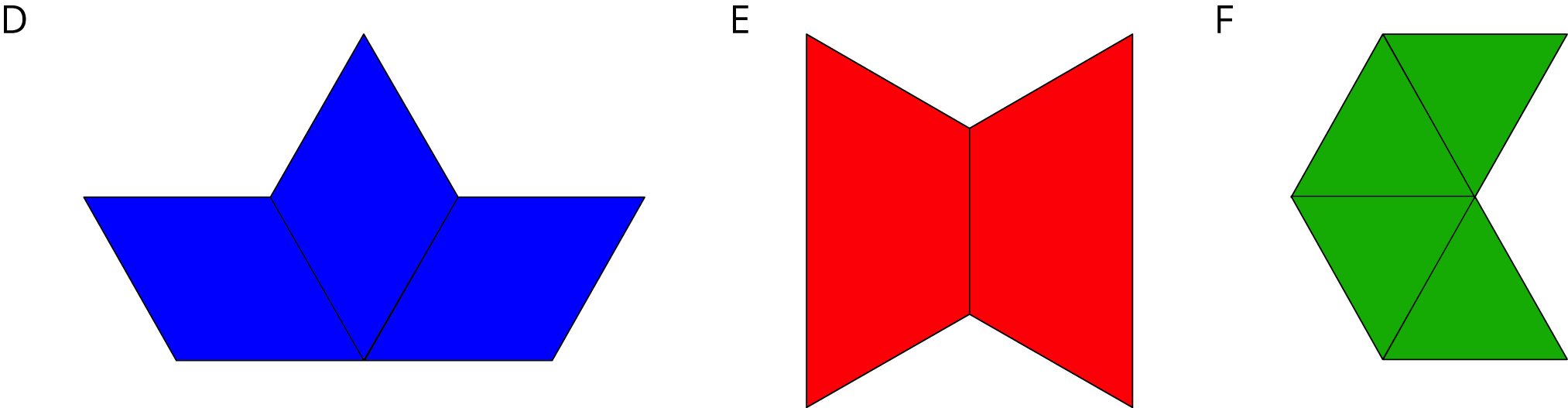
6.1: Scaling a Pattern Block
Use the applets to explore the pattern blocks. Work with your group to build the scaled copies described in each question.

- How many blue rhombus blocks does it take to build a scaled copy of Figure A:
-
Where each side is twice as long?
-
Where each side is 3 times as long?
-
Where each side is 4 times as long?
-
- How many green triangle blocks does it take to build a scaled copy of Figure B:
-
Where each side is twice as long?
-
Where each side is 3 times as long?
-
Using a scale factor of 4?
-
- How many red trapezoid blocks does it take to build a scaled copy of Figure C:
-
Using a scale factor of 2?
-
Using a scale factor of 3?
-
Using a scale factor of 4?
-
- Make a prediction: How many blocks would it take to build scaled copies of these shapes using a scale factor of 5? Using a scale factor of 6? Be prepared to explain your reasoning.