
Unit 1: Practice Problem Sets
Lesson 1
Problem 1
Here is a figure that looks like the letter A, along with several other figures. Which figures are scaled copies of the original A? Explain how you know.
Problem 2
Tyler says that Figure B is a scaled copy of Figure A because all of the peaks are half as tall.
Do you agree with Tyler? Explain your reasoning.
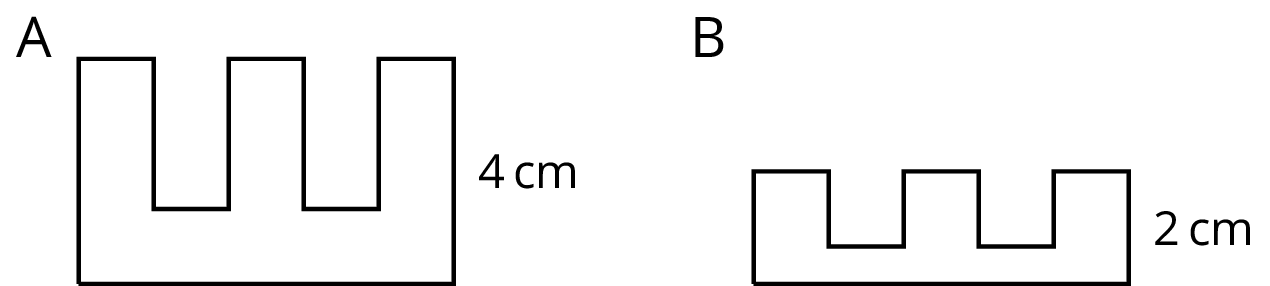
Problem 3
Here is a picture of the Rose Bowl Stadium in Pasadena, CA.

Here are some copies of the picture. Select all the pictures that are scaled copies of the original picture.

Problem 4
Complete each equation with a number that makes it true.
- 5 \boldcdot \text{______} = 15
- 4 \boldcdot \text{______} = 32
- 6 \boldcdot \text{______} = 9
- 12 \boldcdot \text{______} = 3
Lesson 2
Problem 1
The second H-shaped polygon is a scaled copy of the first.
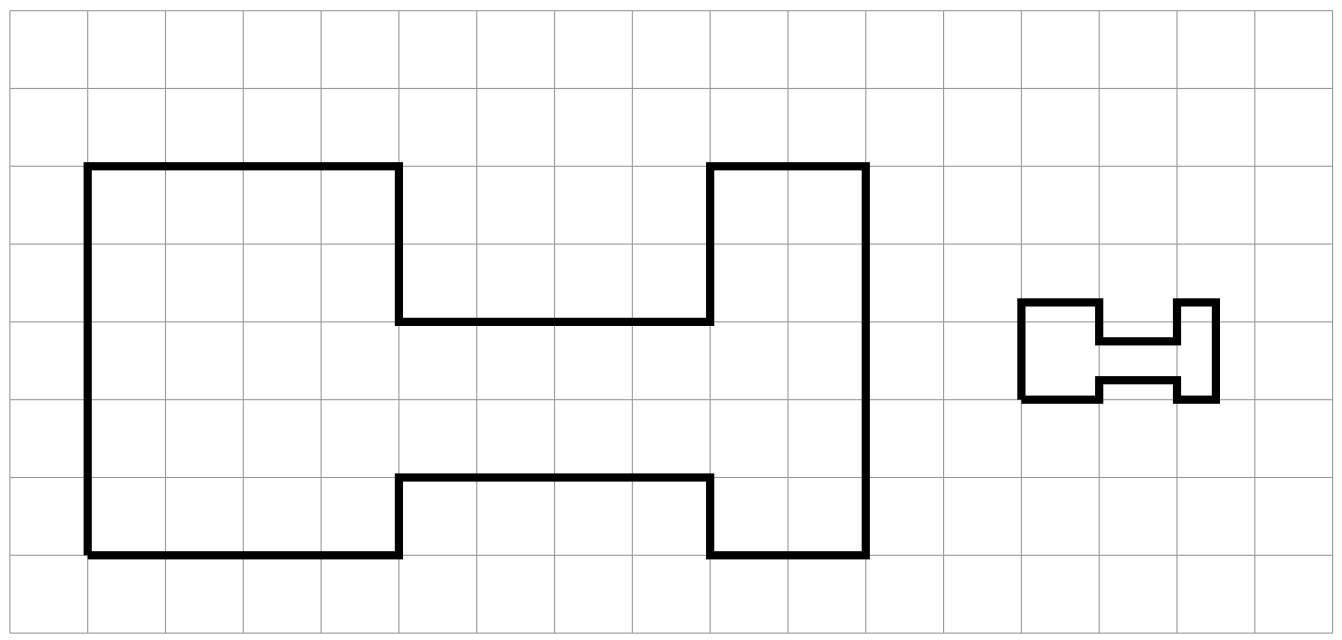
-
Show one pair of corresponding points and two pairs of corresponding sides in the original polygon and its copy. Consider using colored pencils to highlight corresponding parts or labeling some of the vertices.
-
What scale factor takes the original polygon to its smaller copy? Explain or show your reasoning.
Problem 2
Figure B is a scaled copy of Figure A. Select all of the statements that must be true:
- Figure B is larger than Figure A.
- Figure B has the same number of edges as Figure A.
- Figure B has the same perimeter as Figure A.
- Figure B has the same number of angles as Figure A.
- Figure B has angles with the same measures as Figure A.
Problem 3
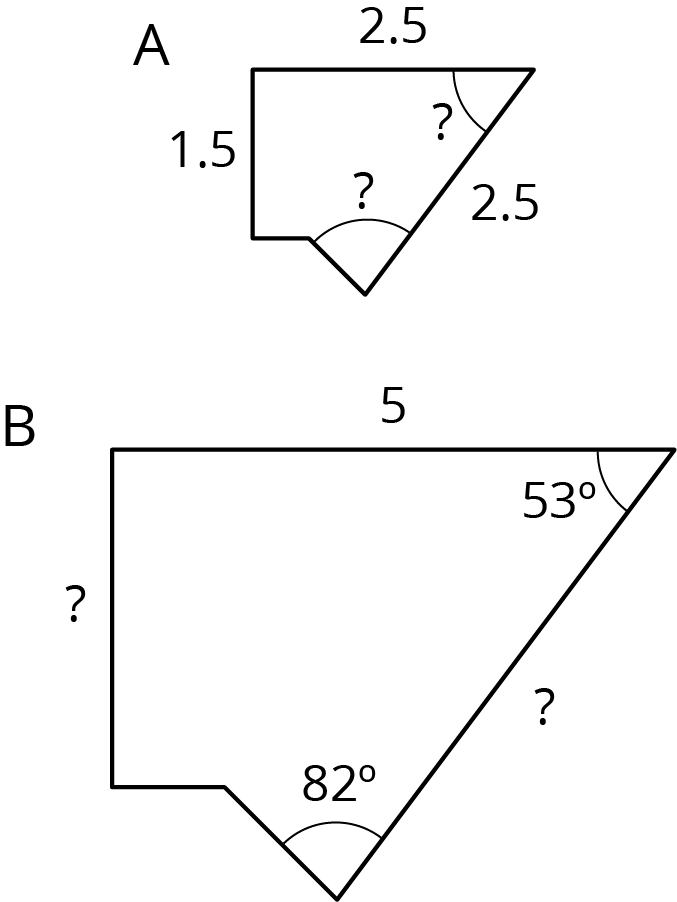
Polygon B is a scaled copy of Polygon A.
-
What is the scale factor from Polygon A to Polygon B? Explain your reasoning.
-
Find the missing length of each side marked with ? in Polygon B.
-
Determine the measure of each angle marked with ? in Polygon A.
Problem 4
Complete each equation with a number that makes it true.
- 8 \boldcdot \text{______} = 40
- 8 + \text{______} = 40
- 21 \div \text{______} = 7
- 21 - \text{______} = 7
- 21 \boldcdot \text{______} = 7
Lesson 3
Problem 1
Here are 3 polygons.
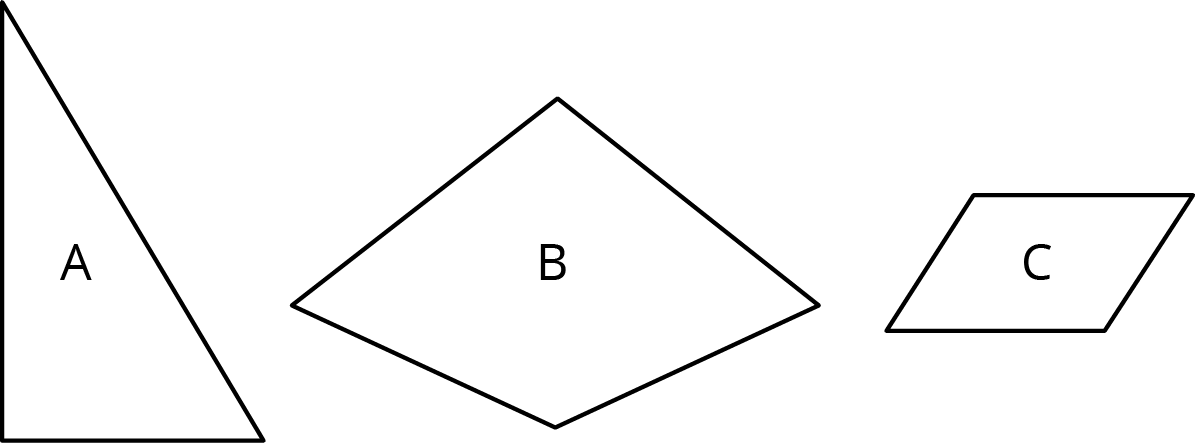
Draw a scaled copy of Polygon A using a scale factor of 2.
Draw a scaled copy of Polygon B using a scale factor of \frac{1}{2}.
Draw a scaled copy of Polygon C using a scale factor of \frac{3}{2}.
Problem 2
Problem 3
Here is a polygon on a grid.
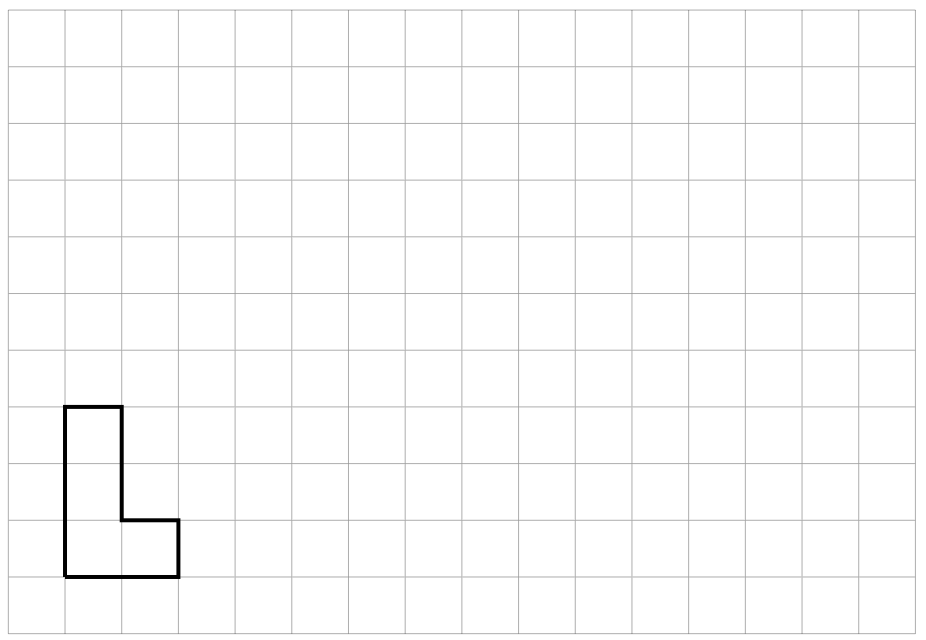
Draw a scaled copy of this polygon that has a perimeter of 30 units. What is the scale factor? Explain how you know.
Problem 4 (from Unit 1, Lesson 1)
Priya and Tyler are discussing the figures shown below. Priya thinks that B, C, and D are scaled copies of A. Tyler says B and D are scaled copies of A. Do you agree with Priya, or do you agree with Tyler? Explain your reasoning.

Lesson 4
Problem 1
Select all the statements that must be true for any scaled copy Q of Polygon P.
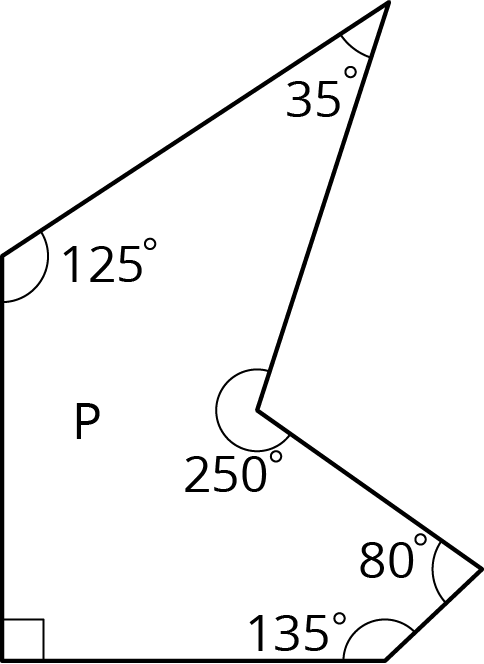
-
The side lengths are all whole numbers.
-
The angle measures are all whole numbers.
-
Q has exactly 1 right angle.
-
If the scale factor between P and Q is \frac15, then each side length of P is multiplied by \frac15 to get the corresponding side length of Q.
-
If the scale factor is 2, each angle in P is multiplied by 2 to get the corresponding angle in Q.
-
Q has 2 acute angles and 3 obtuse angles.
Problem 2
Here is Quadrilateral ABCD.
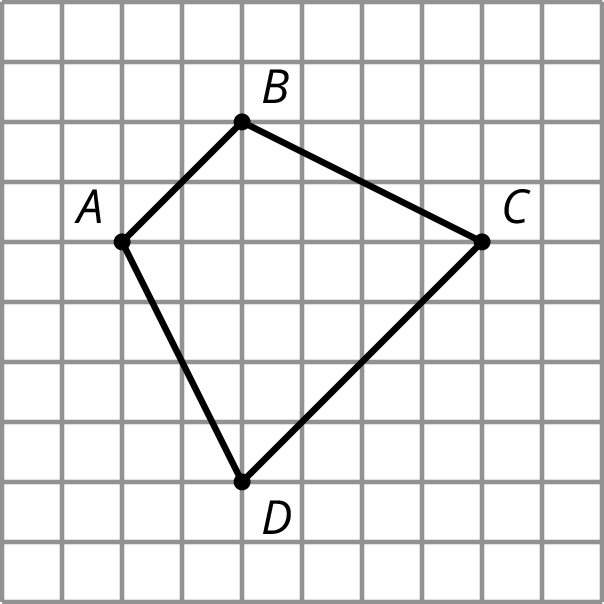
Quadrilateral PQRS is a scaled copy of Quadrilateral ABCD. Point P corresponds to A, Q to B, R to C, and S to D.
If the distance from P to R is 3 units, what is the distance from Q to S? Explain your reasoning.
Problem 3
Figure 2 is a scaled copy of Figure 1.

- Identify the points in Figure 2 that correspond to the points A and C in Figure 1. Label them P and R. What is the distance between P and R?
- Identify the points in Figure 1 that correspond to the points Q and S in Figure 2. Label them B and D. What is the distance between B and D?
- What is the scale factor that takes Figure 1 to Figure 2?
- G and H are two points on Figure 1, but they are not shown. The distance between G and H is 1. What is the distance between the corresponding points on Figure 2?
Problem 4 (from Unit 2, Lesson 4)
To make 1 batch of lavender paint, the ratio of cups of pink paint to cups of blue paint is 6 to 5. Find two more ratios of cups of pink paint to cups of blue paint that are equivalent to this ratio.
Lesson 5
Problem 1
Rectangles P, Q, R, and S are scaled copies of one another. For each pair, decide if the scale factor from one to the other is greater than 1, equal to 1, or less than 1.
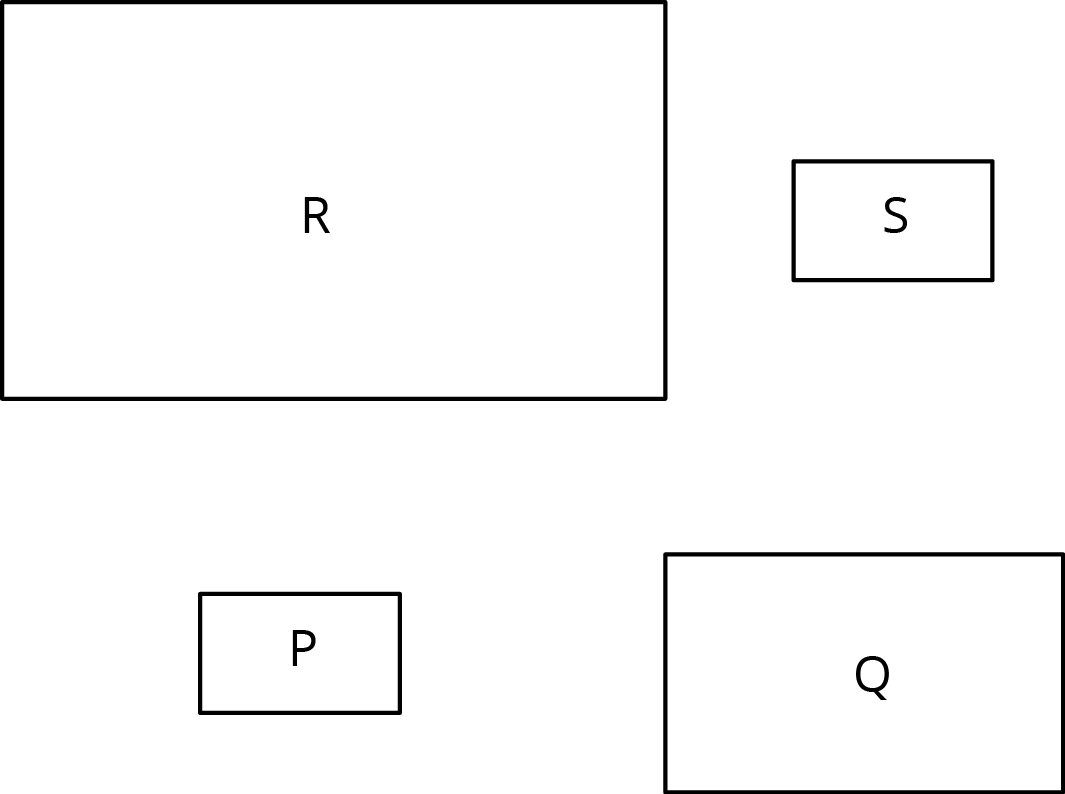
- from P to Q
- from P to R
- from Q to S
- from Q to R
- from S to P
- from R to P
- from P to S
Problem 2
Triangle S and Triangle L are scaled copies of one another.
-
What is the scale factor from S to L?
-
What is the scale factor from L to S?
-
Triangle M is also a scaled copy of S. The scale factor from S to M is \frac{3}{2}. What is the scale factor from M to S?

Problem 3
Are two squares with the same side lengths scaled copies of one another? Explain your reasoning.
Problem 4 (from Unit 1, Lesson 2)
Quadrilateral A has side lengths 2, 3, 5, and 6. Quadrilateral B has side lengths 4, 5, 8, and 10. Could one of the quadrilaterals be a scaled copy of the other? Explain.
Problem 5 (from Unit 2, Lesson 5)
Select all the ratios that are equivalent to the ratio 12:3. Explain how you know.
- 6:1
- 1:4
- 4:1
- 24:6
- 15:6
- 1,200:300
- 112:13
Lesson 6
Problem 1
On the grid, draw a scaled copy of Polygon Q using a scale factor of 2. Compare the perimeter and area of the new polygon to those of Q.

Problem 2
A right triangle has an area of 36 square units.
If you draw scaled copies of this triangle using the scale factors in the table, what will the areas of these scaled copies be? Explain or show your reasoning.
| row 1 | scale factor | area (units2) |
|---|---|---|
| row 2 | 1 | 36 |
| row 3 | 2 | |
| row 4 | 3 | |
| row 5 | 5 | |
| row 6 | \frac12 | |
| row 7 | \frac23 |
Problem 3
Diego drew a scaled version of a Polygon P and labeled it Q.
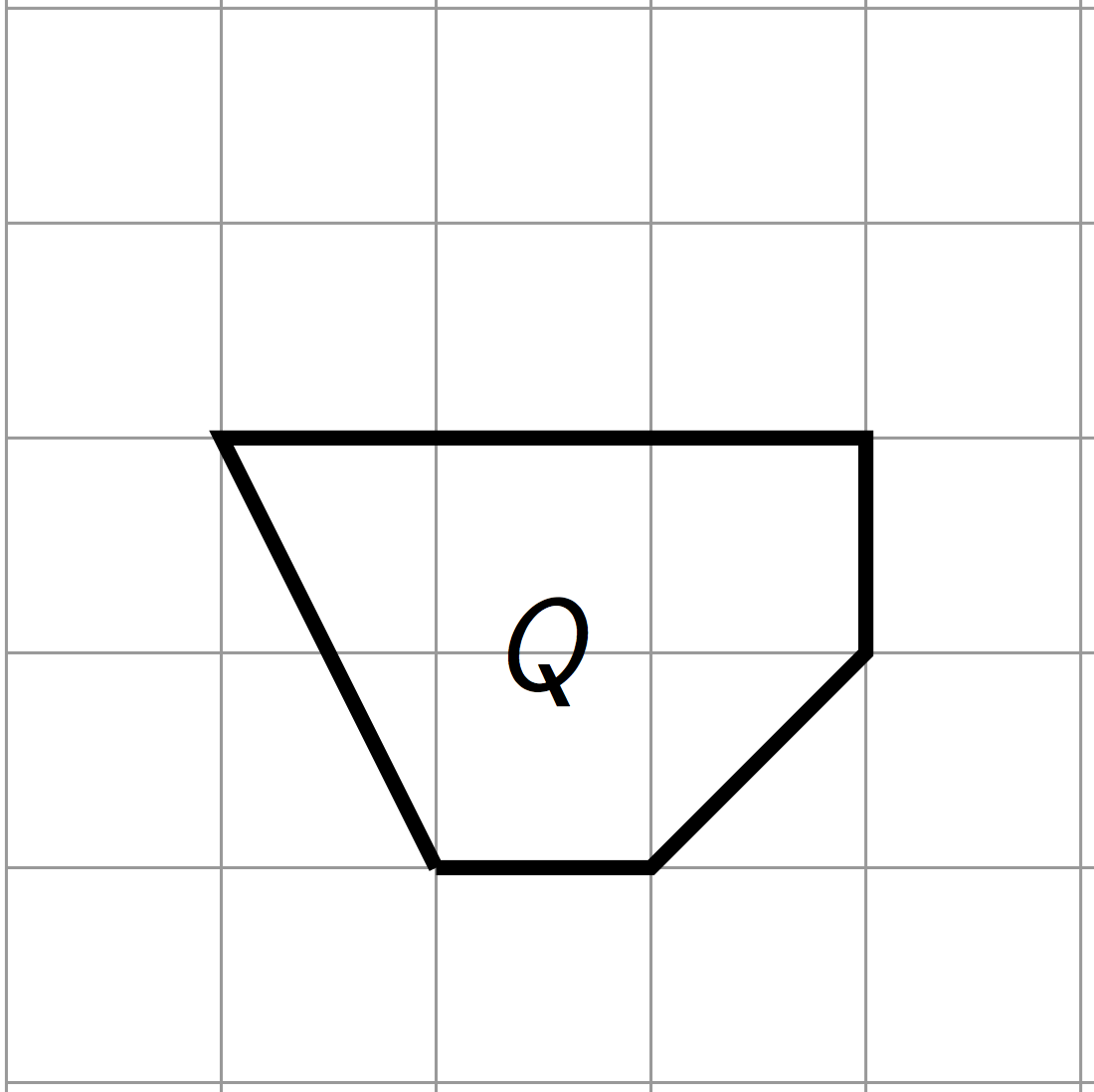
If the area of Polygon P is 72 square units, what scale factor did Diego use to go from P to Q? Explain your reasoning.
Problem 4 (from Unit 1, Lesson 2)
Here is an unlabeled polygon, along with its scaled copies Polygons A–D. For each copy, determine the scale factor. Explain how you know.

Problem 5 (from Unit 1, Lesson 5)
Solve each equation mentally.
- \frac17\boldcdot x=1
- x \boldcdot \frac{1}{11}=1
- 1\div \frac{1}{5}=x
Lesson 7
Problem 1
The Westland Lysander was an aircraft used by the Royal Air Force in the 1930s. Here are some scale drawings that show the top, side, and front views of the Lysander.
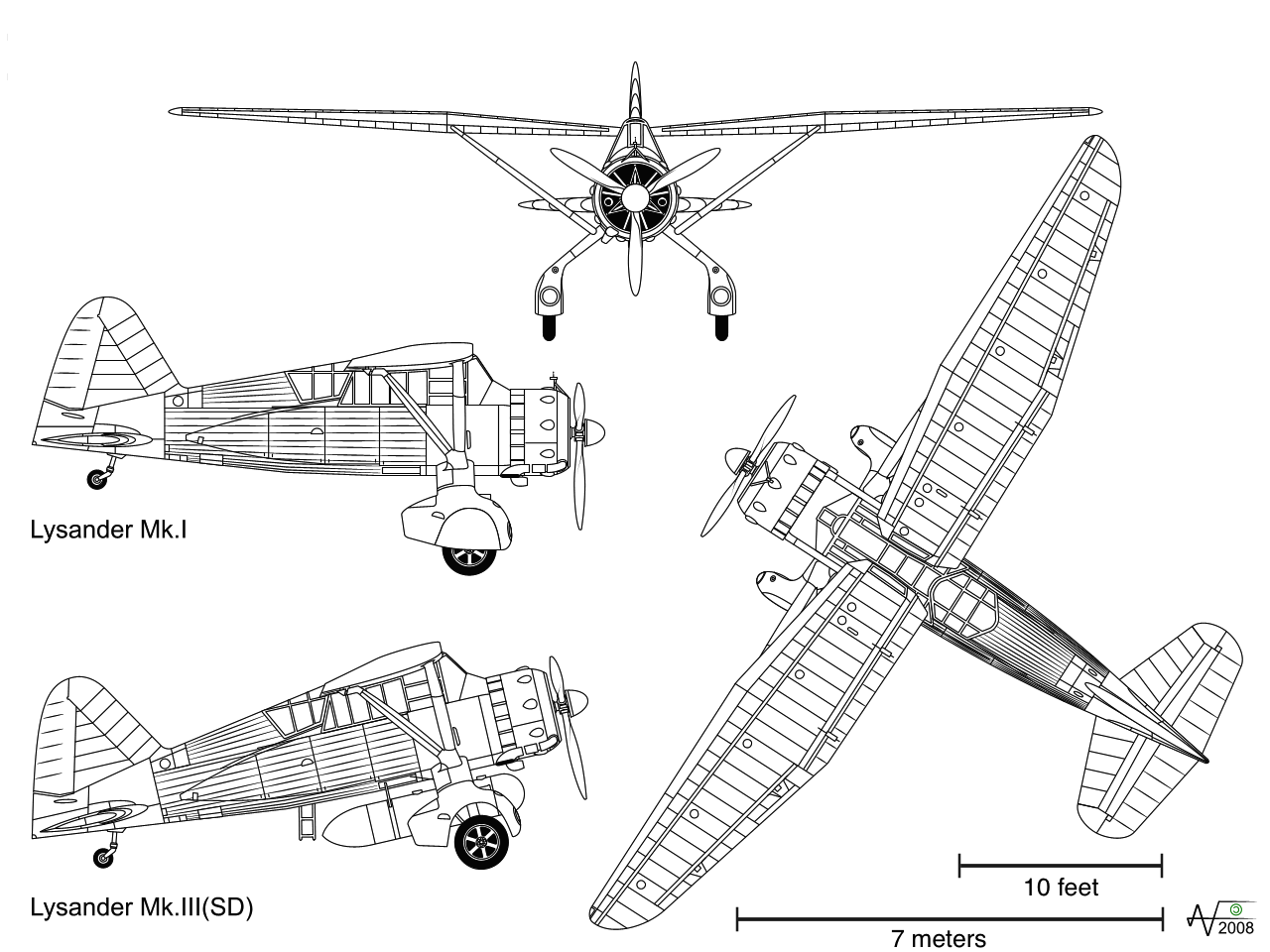
Use the scales and scale drawings to approximate the actual lengths of:
-
the wingspan of the plane, to the nearest foot
-
the height of the plane, to the nearest foot
-
the length of the Lysander Mk. I, to the nearest meter
Problem 2
Problem 3
Here is a scale map of Lafayette Square, a rectangular garden north of the White House.
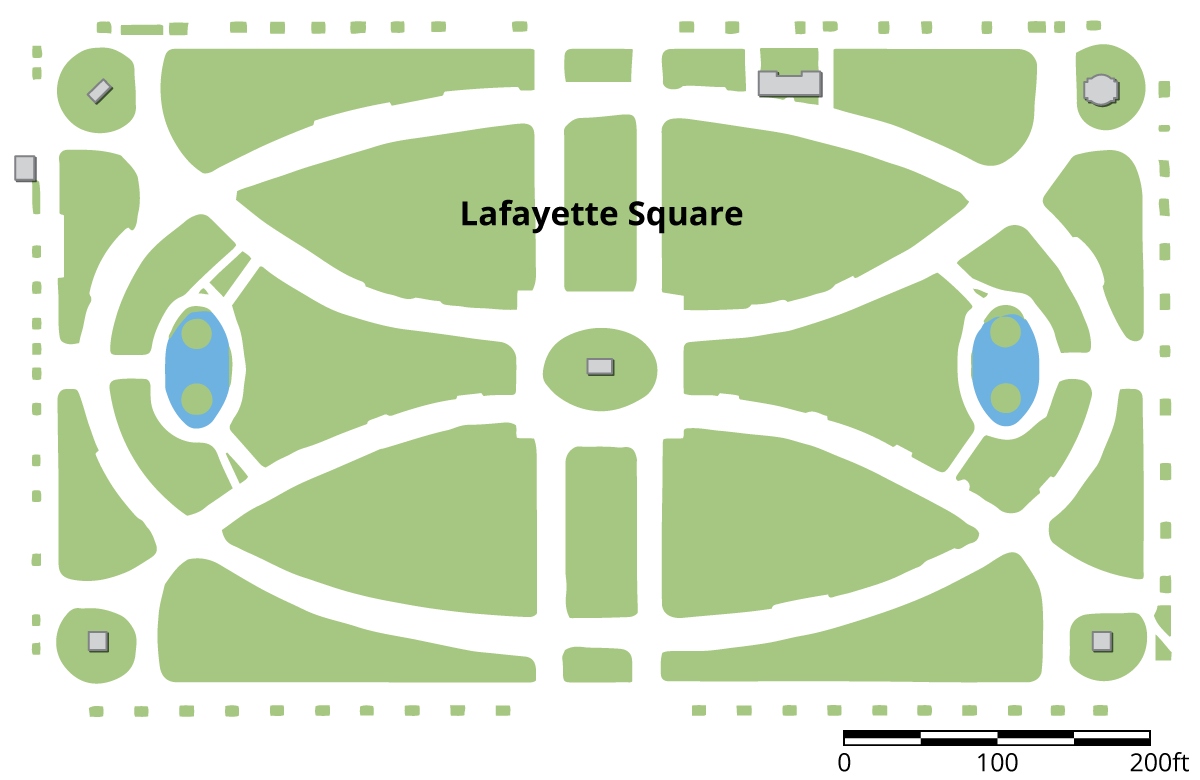
-
The scale is shown in the lower right corner. Find the actual side lengths of Lafayette Square in feet.
-
Use an inch ruler to measure the line segment of the graphic scale. About how many feet does one inch represent on this map?
Problem 4 (from Unit 1, Lesson 6)
Here is Triangle A. Lin created a scaled copy of Triangle A with an area of 72 square units.
-
How many times larger is the area of of the scaled copy compared to that of Triangle A?
-
What scale factor did Lin apply to the Triangle A to create the copy?
-
What is the length of bottom side of the scaled copy?

Lesson 8
Problem 1
Here is a map that shows parts of Texas and Oklahoma.
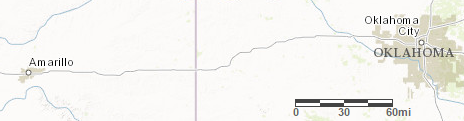
-
About how far is it from Amarillo to Oklahoma City? Explain your reasoning.
-
Driving at a constant speed of 70 miles per hour, will it be possible to make this trip in 3 hours? Explain how you know.
Problem 2
A local park is in the shape of a square. A map of the local park is made with the scale 1 inch to 200 feet.
- If the park is shown as a square on the map, each side of which is one foot long, how long is each side of the square park?
- If a straight path in the park is 900 feet long, how long would the path be when represented on the map?
Lesson 9
Problem 1
An image of a book shown on a website is 1.5 inches wide and 3 inches tall on a computer monitor. The actual book is 9 inches wide.
- What scale is being used for the image?
- How tall is the actual book?
Problem 2
The flag of Colombia is a rectangle that is 6 ft long with three horizontal strips.

- The top stripe is 2 ft tall and is yellow.
- The middle stripe is 1 ft tall and is blue.
- The bottom stripe is also 1 ft tall and is red.
- Create a scale drawing of the Colombian flag with a scale of 1 cm to 2 ft.
- Create a scale drawing of the Colombian flag with a scale of 2 cm to 1 ft.
Problem 3 (from Unit 1, Lesson 6)
These triangles are scaled copies of each other.
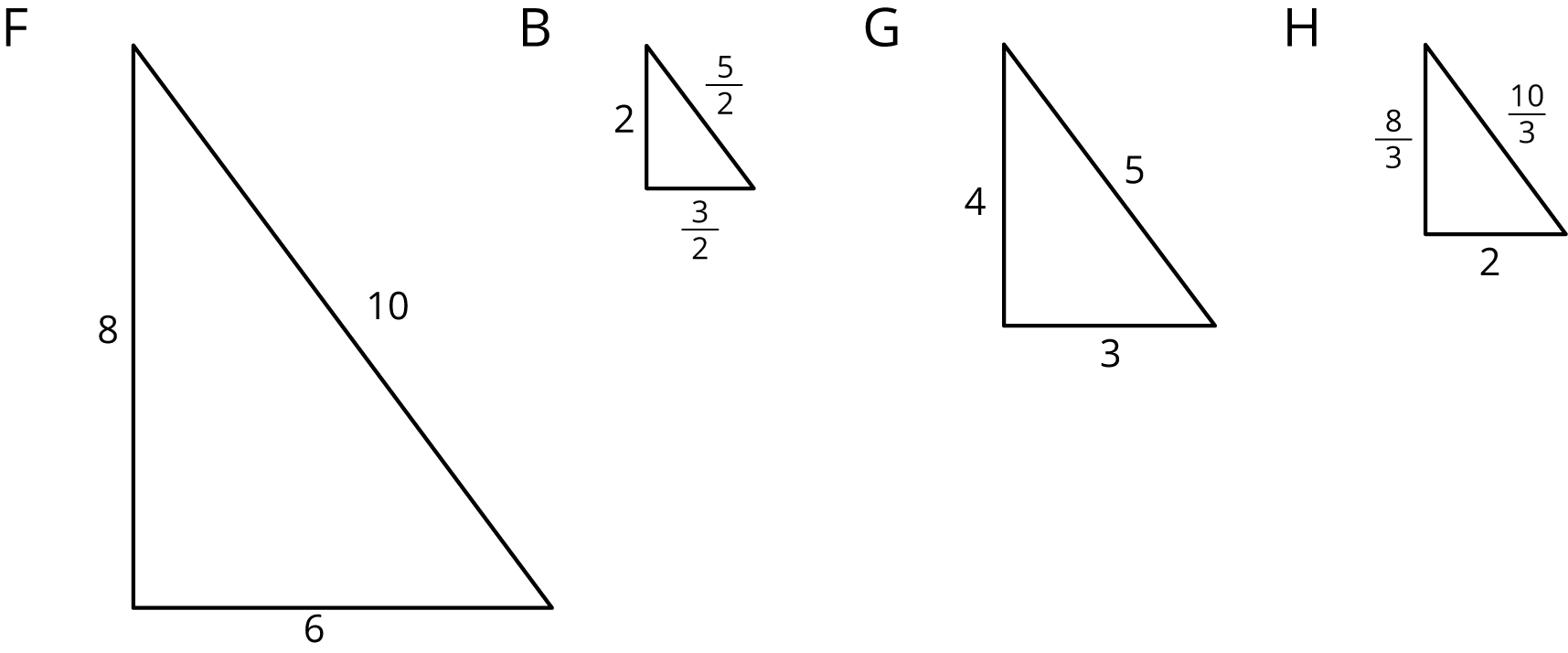
For each pair of triangles listed, the area of the second triangle is how many times larger than the area of the first?
-
Triangle G and Triangle F
-
Triangle G and Triangle B
-
Triangle B and Triangle F
-
Triangle F and Triangle H
-
Triangle G and Triangle H
-
Triangle H and Triangle B
Problem 4 (from Unit 1, Lesson 3)
Here is an unlabeled rectangle, followed by other quadrilaterals that are labeled.
- Select all quadrilaterals that are scaled copies of the unlabeled rectangle. Explain how you know.

- On graph paper, draw a different scaled version of the original rectangle.
Lesson 10
Problem 1
Here is a scale drawing of a swimming pool where 1 cm represents 1 m.

- How long and how wide is the actual swimming pool?
- Will a scale drawing where 1 cm represents 2 m be larger or smaller than this drawing?
- Make a scale drawing of the swimming pool where 1 cm represents 2 m.
Problem 2
A map of a park has a scale of 1 inch to 1,000 feet. Another map of the same park has a scale of 1 inch to 500 feet. Which map is larger? Explain or show your reasoning.
Problem 3
On a map with a scale of 1 inch to 12 feet, the area of a restaurant is 60 in2. Han says that the actual area of the restaurant is 720 ft2. Do you agree or disagree? Explain your reasoning.
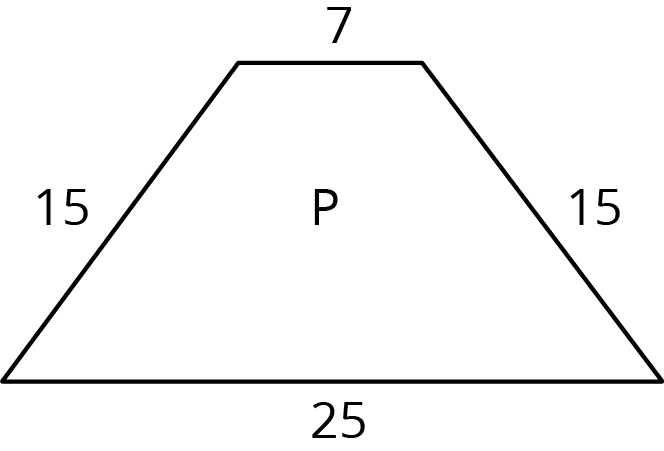
Problem 4 (from Unit 1, Lesson 3)
If Quadrilateral Q is a scaled copy of Quadrilateral P created with a scale factor of 3, what is the perimeter of Q?
Problem 5 (from Unit 1, Lesson 2)
Triangle DEF is a scaled copy of triangle ABC. For each of the following parts of triangle ABC, identify the corresponding part of triangle DEF.
- angle ABC
- angle BCA
- segment AC
- segment BA
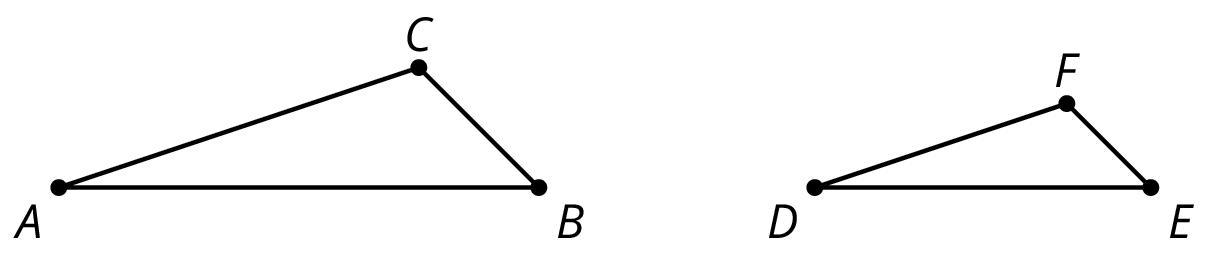
Lesson 11
Problem 1
A scale drawing of a car is presented in the following three scales. Order the scale drawings from smallest to largest. Explain your reasoning. (There are about 1.1 yards in a meter, and 2.54 cm in an inch.)
-
1 in to 1 ft
-
1 in to 1 m
-
1 in to 1 yd
Problem 2
Which scales are equivalent to 1 inch to 1 foot? Select all that apply.
-
1 to 12
-
\frac{1}{12}\text{ to }1
-
100 to 0.12
-
5 to 60
-
36 to 3
-
9 to 108
Problem 3
A model airplane is built at a scale of 1 to 72. If the model plane is 8 inches long, how many feet long is the actual airplane?
Problem 4 (from Unit 1, Lesson 3)
Problem 5 (from Unit 1, Lesson 6)
Polygon B is a scaled copy of Polygon A using a scale factor of 5. Polygon A’s area is what fraction of Polygon B’s area?
Problem 6 (from Unit 1, Lesson 5)
Figures R, S, and T are all scaled copies of one another. Figure S is a scaled copy of R using a scale factor of 3. Figure T is a scaled copy of S using a scale factor of 2. Find the scale factors for each of the following:
- From T to S
- From S to R
- From R to T
- From T to R
Lesson 12
Problem 1
The Empire State Building in New York City is about 1,450 feet high (including the antenna at the top) and 400 feet wide. Andre wants to make a scale drawing of the front view of the Empire State Building on an 8 \frac{1}{2}-inch-by-11-inch piece of paper. Select a scale that you think is the most appropriate for the scale drawing. Explain your reasoning.
- 1 inch to 1 foot
- 1 inch to 100 feet
- 1 inch to 1 mile
- 1 centimeter to 1 meter
- 1 centimeter to 50 meters
- 1 centimeter to 1 kilometer
Problem 2
Elena finds that the area of a house on a scale drawing is 25 square inches. The actual area of the house is 2,025 square feet. What is the scale of the drawing?
Problem 3
Which of these scales are equivalent to 3 cm to 4 km? Select all that apply. Recall that 1 inch is 2.54 centimeters.
-
0.75 cm to 1 km
-
1 cm to 12 km
-
6 mm to 2 km
-
0.3 mm to 40 m
-
1 inch to 7.62 km
Problem 4 (from Unit 1, Lesson 6)
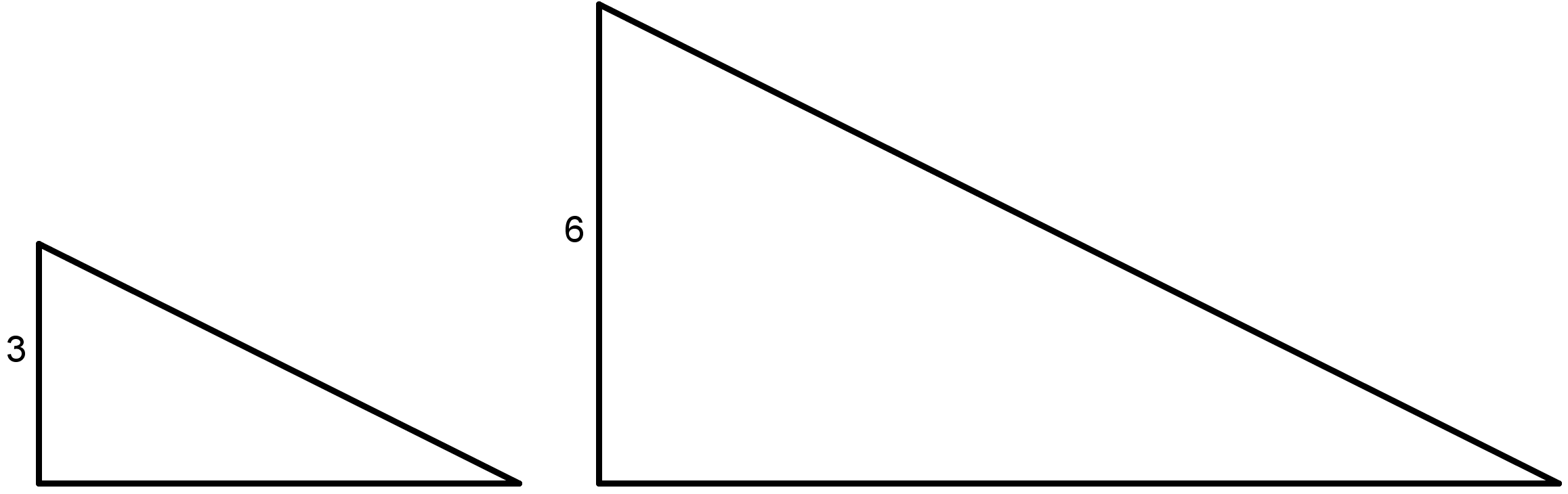
These two triangles are scaled copies of one another. The area of the smaller triangle is 9 square units. What is the area of the larger triangle? Explain or show how you know.
Problem 5 (from Unit 2, Lesson 8)
Water costs $1.25 per bottle. At this rate, what is the cost of:
- 10 bottles?
- 20 bottles?
- 50 bottles?
Problem 6 (from Unit 2, Lesson 11)
The first row of the table shows the amount of dish detergent and water needed to make a soap solution.
-
Complete the table for 2, 3, and 4 batches.
-
How much water and detergent is needed for 8 batches? Explain your reasoning.
| number of batches | cups of water | cups of detergent | |
|---|---|---|---|
| row 1 | 1 | 6 | 1 |
| row 2 | 2 | ||
| row 3 | 3 | ||
| row 4 | 4 |
Lesson 13
No practice problems for this lesson.