
Unit 4: Practice Problem Sets
Lesson 1
Problem 1
A rectangle has a height to width ratio of 3 : 4.5. Give two examples of dimensions for rectangles that could be scaled versions of this rectangle.
Problem 2
One rectangle measures 2 units by 7 units. A second rectangle measures 11 units by 37 units. Are these two figures scaled versions of each other? If so, find the scale factor. If not, briefly explain why.
Problem 3 (from Unit 2, Lesson 5)
Ants have 6 legs. Elena and Andre write equations showing the proportional relationship between the number of ants, a, to the number of ant legs l. Elena writes a = 6 \boldcdot l and Andre writes l = \frac{1}{6} \boldcdot a. Do you agree with either of the equations? Explain your reasoning.
Problem 4 (from Unit 1, Lesson 4)
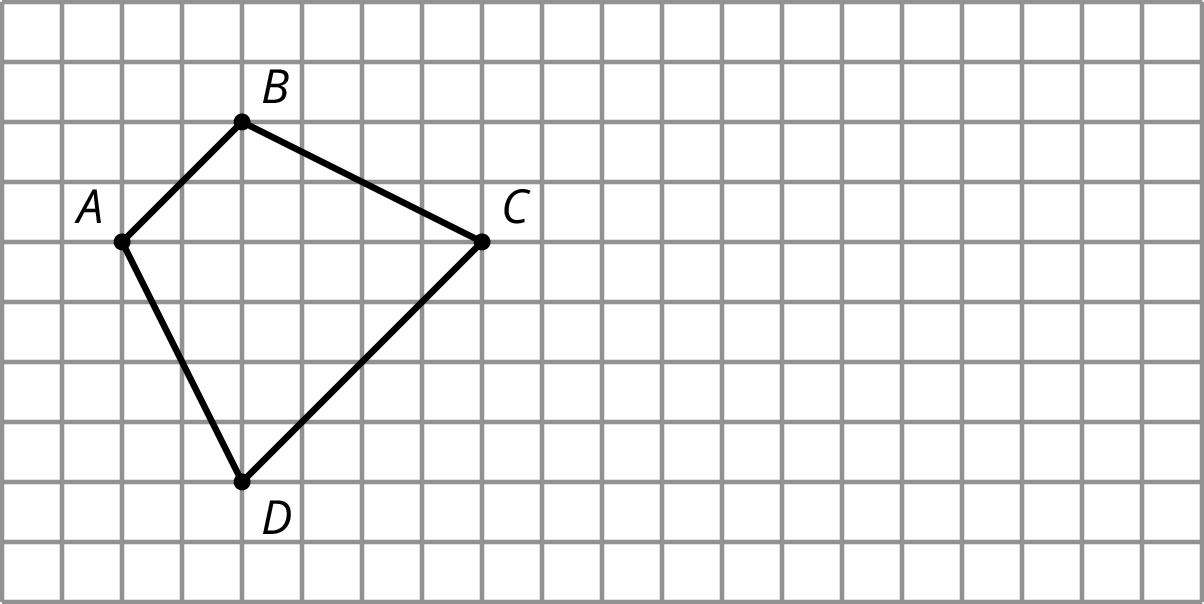
On the grid, draw a scaled copy of quadrilateral ABCD with a scale factor \frac{2}{3}.
Problem 5 (from Unit 1, Lesson 5)
Solve each equation mentally.
- \frac{5}{2} \boldcdot x=1
- x \boldcdot \frac{7}{3}=1
- 1\div \frac{11}{2}=x
Problem 6 (from Unit 1, Lesson 11)
Lin has a scale model of a modern train. The model is created at a scale of 1 to 48.
-
The height of the model train is 102 millimeters. What is the actual height of the train in meters? Explain your reasoning.
-
On the scale model, the distance between the wheels on the left and the wheels on the right is 1\frac14 inches. The state of Wyoming has old railroad tracks that are 4.5 feet apart. Can the modern train travel on those tracks? Explain your reasoning.
Lesson 2
Problem 1
A cyclist rode 3.75 miles in 0.3 hours.
- How fast was she going in miles per hour?
- At that rate, how long will it take her to go 4.5 miles?
Problem 2
A recipe for sparkling grape juice calls for 1\frac12 quarts of sparkling water and \frac34 quart of grape juice.
- How much sparkling water would you need to mix with 9 quarts of grape juice?
- How much grape juice would you need to mix with \frac{15}{4} quarts of sparkling water?
- How much of each ingredient would you need to make 100 quarts of punch?
Problem 3 (from Unit 3, Lesson 10)
- Draw a scaled copy of the circle using a scale factor of 2.
- How does the circumference of the scaled copy compare to the circumference of the original circle?
- How does the area of the scaled copy compare to the area of the original circle?
Problem 4
At a deli counter,
- Someone bought 1 \frac34 pounds of ham for $14.50.
- Someone bought 2 \frac12 pounds of turkey for $26.25.
- Someone bought \frac38 pounds of roast beef for $5.50.
Which meat is the least expensive per pound? Which meat is the most expensive per pound? Explain how you know.
Problem 5 (from Unit 1, Lesson 11)
Jada has a scale map of Kansas that fits on a page in her book. The page is 5 inches by 8 inches. Kansas is about 210 miles by 410 miles. Select all scales that could be a scale of the map. (There are 2.54 centimeters in an inch.)
-
1 in to 1 mi
-
1 cm to 1 km
-
1 in to 10 mi
-
1 ft to 100 mi
-
1 cm to 200 km
-
1 in to 100 mi
-
1 cm to 1000 km
Lesson 3
Problem 1
It takes an ant farm 3 days to consume \frac12 of an apple. At that rate, in how many days will the ant farm consume 3 apples?
Problem 2
To make a shade of paint called jasper green, mix 4 quarts of green paint with \frac23 cups of black paint. How much green paint should be mixed with 4 cups of black paint to make jasper green?
Problem 3
An airplane is flying from New York City to Los Angeles. The distance it travels in miles, d, is related to the time in seconds, t, by the equation d=0.15t.
- How fast is it flying? Be sure to include the units.
- How far will it travel in 30 seconds?
- How long will it take to go 12.75 miles?
Problem 4
A grocer can buy strawberries for $1.38 per pound.
- Write an equation relating c, the cost, and p, the pounds of strawberries.
- A strawberry order cost $241.50. How many pounds did the grocer order?
Problem 5 (from Unit 3, Lesson 10)
Crater Lake in Oregon is shaped like a circle with a diameter of about 5.5 miles.
-
How far is it around the perimeter of Crater Lake?
-
What is the area of the surface of Crater Lake?
Problem 6 (from Unit 3, Lesson 8)
A 50-centimeter piece of wire in bent into a circle. What is the area of this circle?
Problem 7 (from Unit 1, Lesson 2)
Suppose Quadrilaterals A and B are both squares. Are A and B necessarily scale copies of one another? Explain.
Lesson 4
Problem 1
Match each situation with a diagram.
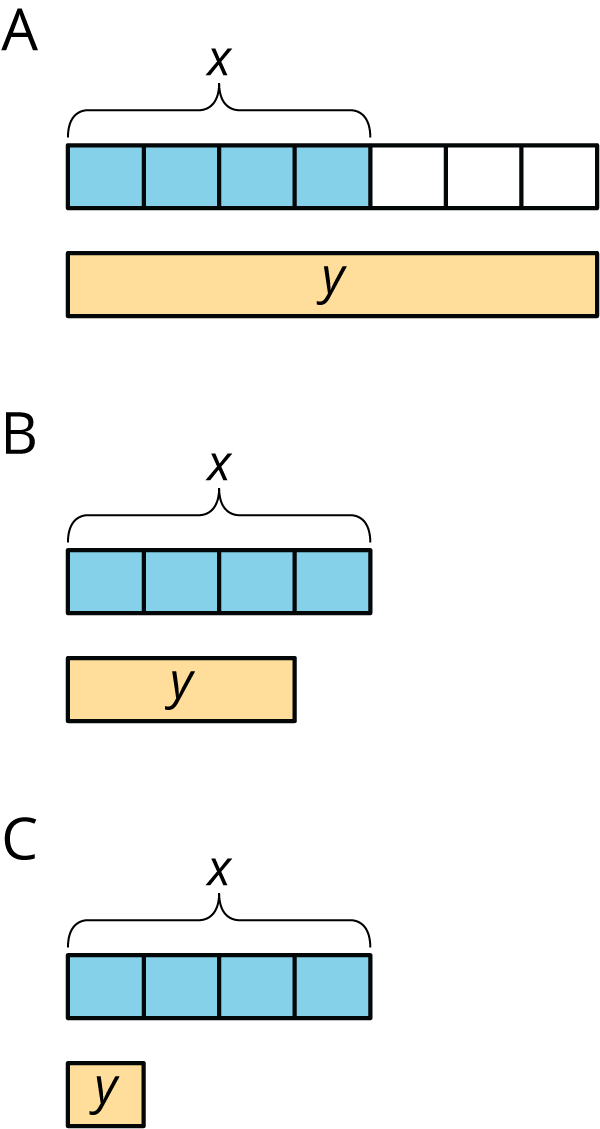
- Diego drank x ounces of juice. Lin drank \frac14 less than that.
- Lin ran x miles. Diego ran \frac34 more than that.
- Diego bought x pounds of almonds. Lin bought \frac14 of that.
Problem 2
Elena walked 12 miles. Then she walked \frac{1}{4} that distance. How far did she walk all together? Select all that apply.
-
12 + \frac14
-
12 \boldcdot \frac14
-
12+\frac14 \boldcdot 12
-
12\left(1+\frac14 \right)
-
12 \boldcdot \frac34
-
12 \boldcdot \frac54
Problem 3
Write a story that can be represented by the equation y=x+\frac14x.
Problem 4 (from Unit 4, Lesson 1)
Select all ratios that are equivalent to 4 : 5.
- 2 : 2.5
- 2 : 3
- 3 : 3.75
- 7 : 8
- 8 : 10
- 14 : 27.5
Problem 5 (from Unit 3, Lesson 10)
Jada is making circular birthday invitations for her friends. The diameter of the circle is 12 cm. She bought 180 cm of ribbon to glue around the edge of each invitation. How many invitations can she make?
Lesson 5
Problem 1
- Match each diagram with a description and an equation.
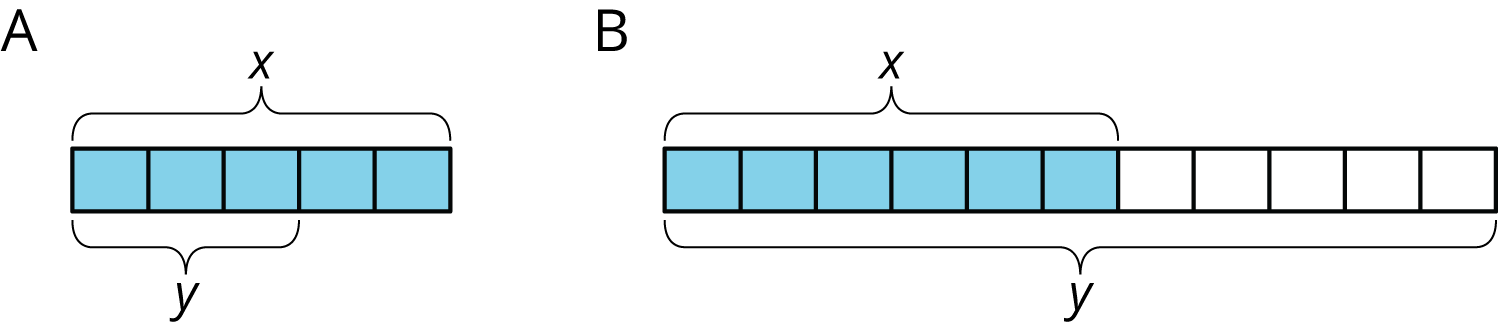
Descriptions:
An increase by \frac23
An increase by \frac{5}{6}
A decrease by \frac25
A decrease by \frac{5}{11}
Equations:
y=1.8\overline{3}x
y=1.\overline{6}x
y=0.6x
y=0.4x
- Draw a diagram for one of the unmatched equations.
Problem 2
At the beginning of the month, there were 80 ounces of peanut butter in the pantry. Since then, the family ate 0.3 of the peanut butter. How many ounces of peanut butter are in the pantry now?
-
0.7 \boldcdot 80
-
0.3 \boldcdot 80
-
80 - 0.3
-
\left(1+ 0.3\right)\boldcdot 80
Problem 3 (from Unit 4, Lesson 4)
- On a hot day, a football team drank an entire 50-gallon cooler of water and half as much again. How much water did they drink?
- Jada has 12 library books checked out and Han has \frac13 less than that. How many books does Han have checked out?
Problem 4 (from Unit 4, Lesson 4)
If x represents a positive number, select all expressions whose value is greater than x.
-
\left(1-\frac14\right)x
-
\left(1+\frac14\right)x
-
\frac78x
-
\frac98x
Problem 5 (from Unit 2, Lesson 6)
A person's resting heart rate is typically between 60 and 100 beats per minute. Noah looks at his watch, and counts 8 heartbeats in 10 seconds.
- Is his heart rate typical? Explain how you know.
- Write an equation for h, the number of times Noah’s heart beats (at this rate) in m minutes.
Lesson 6
Problem 1
For each diagram, decide if y is an increase or a decrease relative to x. Then determine the percent increase or decrease.

Problem 2
Draw diagrams to represent the following situations.
- The amount of flour that the bakery used this month was a 40% increase relative to last month.
- The amount of milk that the bakery used this month was a 75% decrease relative to last month.
Problem 3
Write each percent increase or decrease as a percentage of the initial amount. The first one is done for you.
-
This year, there was 40% more snow than last year.
The amount of snow this year is 140% of the amount of snow last year.
- This year, there were 25% fewer sunny days than last year.
- Compared to last month, there was a 50% increase in the number of houses sold this month.
- The runner’s time to complete the marathon was a 10% less than the time to complete the last marathon.
Problem 4 (from Unit 3, Lesson 3)
The graph shows the relationship between the diameter and the circumference of a circle with the point (1,\pi) shown. Find 3 more points that are on the line.

Problem 5 (from Unit 4, Lesson 4)
Priya bought x grams of flour. Clare bought \frac38 more than that. Select all equations that represent the relationship between the amount of flour that Priya bought, x, and the amount of flour that Clare bought, y.
- y=\frac38 x
- y=\frac58 x
- y=x+\frac38x
- y=x -\frac38 x
- y=\frac{11}{8}x
Lesson 7
Problem 1
A bakery used 25% more butter this month than last month. If the bakery used 240 kilograms of butter last month, how much did it use this month?
Problem 2
Last week, the price of oranges at the farmer's market was $1.75 per pound. This week, the price has decreased by 20%. What is the price of oranges this week?
Problem 3
Noah thinks the answers to these two questions will be the same. Do you agree with him? Explain your reasoning.
- This year, a herd of bison had a 10% increase in population. If there were 550 bison in the herd last year, how many are in the herd this year?
- This year, another herd of bison had a 10% decrease in population. If there are 550 bison in the herd this year, how many bison were there last year?
Problem 4 (from Unit 4, Lesson 5)
Elena walked 12 miles. Then she walked 0.25 that distance. How far did she walk all together? Select all that apply.
- 12+0.25 \boldcdot 12
- 12\left(1+0.25\right)
- 12 \boldcdot 1.25
- 12 \boldcdot 0.25
- 12 + 0.25
Problem 5 (from Unit 3, Lesson 8)
A circle’s circumference is 600 m. What is a good approximation of the circle’s area?
- 300 m2
- 3,000 m2
- 30,000 m2
- 300,000 m2
Problem 6 (from Unit 2, Lesson 6)
The equation d = 3t represents the relationship between the distance (d) in inches that a snail is from a certain rock and the time (t) in minutes.
- What does the number 3 represent?
- How many minutes does it take the snail to get 9 inches from the rock?
- How far will the snail be from the rock after 9 minutes?
Lesson 8
Problem 1
A pair of designer sneakers was purchased for $120. Since they were purchased, their price has increased by 15%. What is the new price?
Problem 2
Elena’s aunt bought her a $150 savings bond when she was born. When Elena is 20 years old, the bond will have earned 105% in interest. How much will the bond be worth when Elena is 20 years old?
Problem 3
In a video game, Clare scored 50% more points than Tyler. If c is the number of points that Clare scored and t is the number of points that Tyler scored, which equations are correct? Select all that apply.
- c = 1.5t
- c = t + 0.5
- c = t + 0.5t
- c = t + 50
- c = (1 + 0.5)t
Problem 4 (from Unit 4, Lesson 6)
Draw a diagram to represent each situation:
- The number of miles driven this month was a 30% decrease of the number of miles driven last month.
- The amount of paper that the copy shop used this month was a 25% increase of the amount of paper they used last month.
Problem 5 (from Unit 4, Lesson 5)
Which decimal is the best estimate of the fraction \frac{29}{40}?
- 0.5
- 0.6
- 0.7
- 0.8
Problem 6 (from Unit 3, Lesson 3)
Could 7.2 inches and 28 inches be the diameter and circumference of the same circle? Explain why or why not.
Lesson 9
Problem 1
The student government snack shop sold 32 items this week.
| snack type | number of items sold |
|---|---|
| fruit cup | 8 |
| veggie sticks | 6 |
| chips | 14 |
| water | 4 |
For each snack type, what percentage of all snacks sold were of that type?
Problem 2
Select all the options that have the same value as 3\frac12\% of 20.
-
3.5% of 20
-
3\frac12 \boldcdot 20
-
(0.35) \boldcdot 20
-
(0.035) \boldcdot 20
-
7% of 10
Problem 3
22% of 65 is 14.3. What is 22.6% of 65? Explain your reasoning.
Problem 4 (from Unit 4, Lesson 7)
Problem 5 (from Unit 4, Lesson 6)
Match each diagram to a situation. The diagrams can be used more than once.
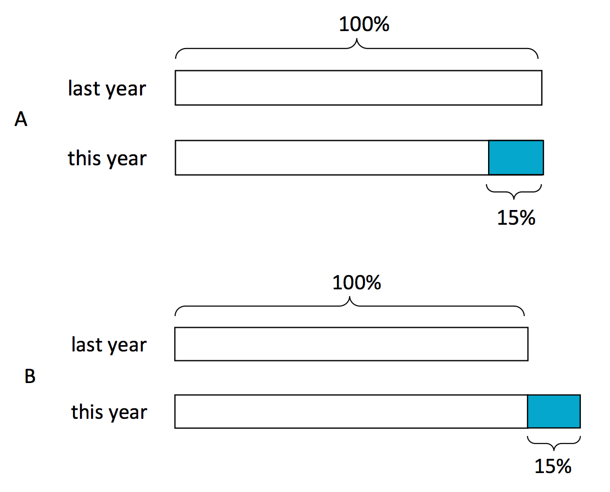
- The amount of apples this year decreased by 15% compared with last year's amount.
- The amount of pears this year is 85% of last year's amount.
- The amount of cherries this year increased by 15% compared with last year's amount.
- The amount of oranges this year is 115% of last year's amount.
Problem 6 (from Unit 2, Lesson 6)
A certain type of car has room for 4 passengers.
- Write an equation relating the number of cars (n) to the number of passengers (p).
- How many passengers could fit in 78 cars?
- How many cars would be needed to fit 78 passengers?
Lesson 10
Problem 1
In a city in Ohio, the sales tax rate is 7.25%. Complete the table to show the sales tax and the total price including tax for each item.
| item |
price before tax ($) |
sales tax ($) | price including tax ($) |
|---|---|---|---|
| pillow | 8.00 | ||
| blanket | 22.00 | ||
| trash can | 14.50 |
Problem 2
The sales tax rate in New Mexico is 5.125%. Select all the equations that represent the sales tax, t, you would pay in New Mexico for an item of cost c?
- t=5.125c
- t=0.5125c
- t=0.05125c
- t=c \div 0.05125
- t=\frac{5.125}{100}c
Problem 3
Here are the prices of some items and the amount of sales tax charged on each in Nevada.
| row 1 | cost of item ($) | sales tax ($) |
|---|---|---|
| row 2 | 10 | 0.46 |
| row 3 | 50 | 2.30 |
| row 4 | 5 | 0.23 |
- What is the sales tax rate in Nevada?
- Write an expression for the amount of sales tax charged, in dollars, on an item that costs c dollars.
Problem 4 (from Unit 4, Lesson 9)
Find each amount:
3.8% of 25
0.2% of 50
180.5% of 99
Problem 5 (from Unit 4, Lesson 8)
On Monday, the high was 60 degrees Fahrenheit. On Tuesday, the high was 18% more. How much did the high increase from Monday to Tuesday?
Problem 6 (from Unit 3, Lesson 4)
Complete the table. Explain or show your reasoning.
| object | radius | circumference |
|---|---|---|
| ceiling fan | 2.8 ft | |
| water bottle cap | 13 mm | |
| bowl | 56.5 cm | |
| drum | 75.4 in |
Lesson 11
Problem 1
A car dealership pays $8,350 for a car. They mark up the price by 17.4% to get the retail price. What is the retail price of the car at this dealership?
Problem 2
A store has a 20% off sale on pants. With this discount, the price of one pair of pants before tax is $15.20. What was the original price of the pants?
- $3.04
- $12.16
- $18.24
- $19.00
Problem 3
Lin is shopping for a couch with her dad and hears him ask the salesperson, “How much is your commission?” The salesperson says that her commission is 5\frac12\% of the selling price.
- How much commission will the salesperson earn by selling a couch for $495?
- How much money will the store get from the sale of the couch?
Problem 4 (from Unit 4, Lesson 9)
A college student takes out a $7,500 loan from a bank. What will the balance of the loan be after one year (assuming the student has not made any payments yet):
- if the bank charges 3.8% interest each year?
- if the bank charges 5.3% interest each year?
Problem 5 (from Unit 4, Lesson 5)
Match the situations with the equations.
- Mai slept for x hours, and Kiran slept for \frac{1}{10} less than that.
- Kiran practiced the piano for x hours, and Mai practiced for \frac25 less than that.
- Mai drank x oz of juice and Kiran drank \frac43 more than that.
- Kiran spent x dollars and Mai spent \frac14 less than that.
- Mai ate x grams of almonds and Kiran ate 1.5 times more than that.
- Kiran collected x pounds of recycling and Mai collected \frac{3}{10} less than that.
- Mai walked x kilometers and Kiran walked \frac38 more than that.
- Kiran completed x puzzles and Mai completed \frac35 more than that.
y=2.33x
y=1.375x
y=0.6x
y=0.9x
y=0.75x
y=1.6x
y=0.7x
y=2.5x
Lesson 12
Problem 1
A music store marks up the instruments it sells by 30%.
- If the store bought a guitar for $45, what will be its store price?
- If the price tag on a trumpet says $104, how much did the store pay for it?
- If the store paid $75 for a clarinet and sold it for $100, did the store mark up the price by 30%?
Problem 2
A family eats at a restaurant. The bill is $42. The family leaves a tip and spends $49.77.
- How much was the tip in dollars?
- How much was the tip as a percentage of the bill?
Problem 3
The price of gold is often reported per ounce. At the end of 2005, this price was $513. At the end of 2015, it was $1060. By what percentage did the price per ounce of gold increase?
Problem 4 (from Unit 2, Lesson 7)
A phone keeps track of the number of steps taken and the distance traveled. Based on the information in the table, is there a proportional relationship between the two quantities? Explain your reasoning.
| number of steps | distance in kilometers | |
|---|---|---|
| row 1 | 950 | 1 |
| row 2 | 2,852 | 3 |
| row 3 | 4,845 | 5.1 |
Problem 5 (from Unit 4, Lesson 4)
Noah picked 3 kg of cherries. Mai picked half as many cherries as Noah. How many total kg of cherries did Mai and Noah pick?
-
3 + \frac12
-
3 - \frac12
-
\left(1+\frac12\right)\boldcdot 3
-
1+\frac12\boldcdot 3
Lesson 13
Problem 1
The depth of a lake is 15.8 m.
- Jada accurately measured the depth of the lake to the nearest meter. What measurement did Jada get?
- By how many meters does the measured depth differ from the actual depth?
- Express the measurement error as a percentage of the actual depth.
Problem 2
A watermelon weighs 8,475 grams. A scale measured the weight with an error of 12% under the actual weight. What was the measured weight?
Problem 3
Noah's oven thermometer gives a reading that is 2% greater than the actual temperature.
- If the actual temperature is 325^\circ\text{F}, what will the thermometer reading be?
- If the thermometer reading is 76^\circ\text{F}, what is the actual temperature?
Problem 4 (from Unit 4, Lesson 4)
At the beginning of the month, there were 80 ounces of peanut butter in the pantry. Now, there is \frac13 less than that. How many ounces of peanut butter are in the pantry now?
- \frac23 \boldcdot 80
- \frac13 \boldcdot 80
- 80-\frac13
- \left(1+\frac13\right)\boldcdot 80
Problem 5 (from Unit 3, Lesson 7)
- Fill in the table for side length and area of different squares.
side length (cm) area (cm2) row 1 3 row 2 100 row 3 25 row 4 s - Is the relationship between the side length of a square and the area of a square proportional?
Lesson 14
Problem 1
A student estimated that it would take 3 hours to write a book report, but it actually took her 5 hours. What is the percent error for her estimate?
Problem 2
A radar gun measured the speed of a baseball at 103 miles per hour. If the baseball was actually going 102.8 miles per hour, what was the percent error in this measurement?
Problem 3
It took 48 minutes to drive downtown. An app estimated it would be less than that. If the error was 20%, what was the app’s estimate?
Problem 4
Problem 5 (from Unit 4, Lesson 4)
For each story, write an equation that describes the relationship between the two quantities.
- Diego collected x kg of recycling. Lin collected \frac25 more than that.
- Lin biked x km. Diego biked \frac{3}{10} less than that.
- Diego read for x minutes. Lin read \frac47 of that.
Problem 6 (from Unit 4, Lesson 12)
For each diagram, decide if y is an increase or a decrease of x. Then determine the percentage.
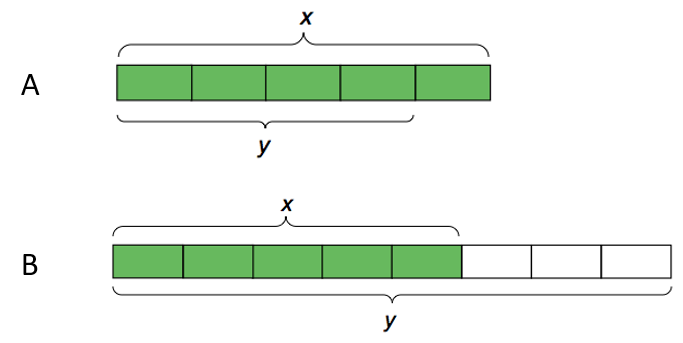
Problem 7 (from Unit 3, Lesson 10)
Lin is making a window covering for a window that has the shape of a half circle on top of a square of side length 3 feet. How much fabric does she need?
Lesson 15
Problem 1
Jada measured the height of a plant in a science experiment and finds that, to the nearest \frac{1}{4} of an inch, it is 4 \frac{3}{4} inches.
- What is the largest the actual height of the plant could be?
- What is the smallest the actual height of the plant could be?
- How large could the percent error in Jada’s measurement be?
Problem 2 (from Unit 2, Lesson 5)
Water is running into a bathtub at a constant rate. After 2 minutes, the tub is filled with 2.5 gallons of water. Write two equations for this proportional relationship. Use w for the amount of water (gallons) and t for time (minutes). In each case, what does the constant of proportionality tell you about the situation?
Problem 3 (from Unit 4, Lesson 5)
Noah picked 3 kg of cherries. Jada picked half as many cherries as Noah. How many total kg of cherries did Jada and Noah pick?
-
3 + 0.5
-
3 - 0.5
-
\left(1+ 0.5 \right)\boldcdot 3
-
1+0.5\boldcdot 3
Problem 4
The reading on a car’s speedometer has 1.6% maximum error. The speed limit on a road is 65 miles per hour.
- The speedometer reads 64 miles per hour. Is it possible that the car is going over the speed limit?
- The speedometer reads 66 miles per hour. Is the car definitely going over the speed limit?
Problem 5 (from Unit 3, Lesson 7)
Here is a shape with some measurements in cm.
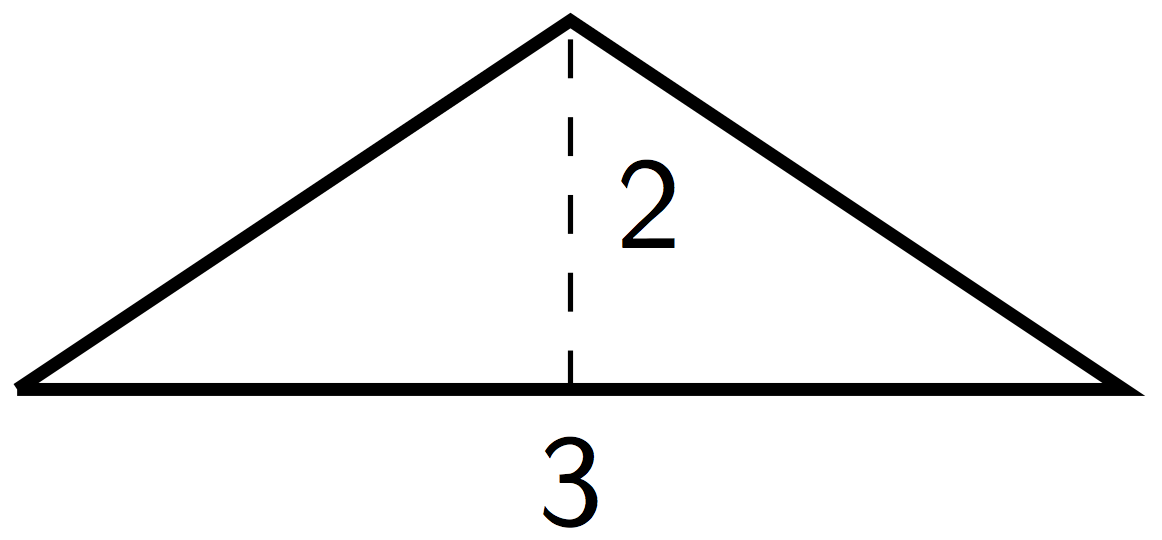
-
Complete the table showing the area of different scaled copies of the triangle.
scale factor area (cm2) row 1 1 row 2 2 row 3 5 row 4 s -
Is the relationship between the scale factor and the area of the scaled copy proportional?
Lesson 16
No practice problems for this lesson.