15.1: A Lot of Iron Ore
An industrial scale is guaranteed by the manufacturer to have a percent error of no more than 1%. What is a possible reading on the scale if you put 500 kilograms of iron ore on it?
Let’s solve more problems about percent error.
An industrial scale is guaranteed by the manufacturer to have a percent error of no more than 1%. What is a possible reading on the scale if you put 500 kilograms of iron ore on it?
A saw mill cuts boards that are 16 ft long. After they are cut, the boards are inspected and rejected if the length has a percent error of 1.5% or more.
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
If your teacher gives you the data card:
Percent error is often used to express a range of possible values. For example, if a box of cereal is guaranteed to have 750 grams of cereal, with a margin of error of less than 5%, what are possible values for the actual number of grams of cereal in the box? The error could be as large as (0.05) \boldcdot 750 = 37.5 and could be either above or below than the correct amount.
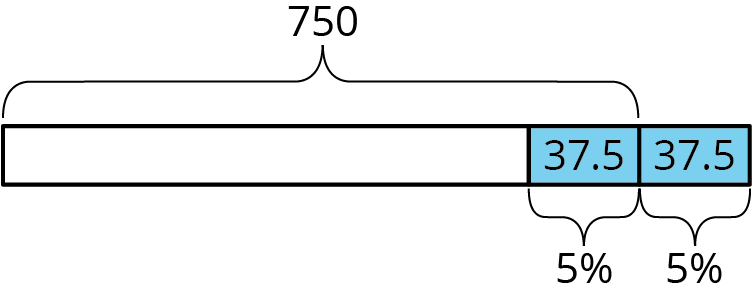
Therefore, the box can have anywhere between 712.5 and 787.5 grams of cereal in it, but it should not have 700 grams or 800 grams, because both of those are more than 37.5 grams away from 750 grams.