Unit 3: Practice Problem Sets
Lesson 1
Problem 1
Estimate the side length of a square that has a 9 cm long diagonal.
Problem 2
Select all quantities that are proportional to the diagonal length of a square.
- Area of a square
- Perimeter of a square
- Side length of a square
Problem 3
Problem 4
The graph shows that while it was being filled, the amount of water in gallons in a swimming pool was approximately proportional to the time that has passed in minutes.
- About how much water was in the pool after 25 minutes?
- Approximately when were there 500 gallons of water in the pool?
- Estimate the constant of proportionality for the number of gallons of water per minute going into the pool.

Lesson 2
Problem 1
Use a geometric tool to draw a circle. Draw and measure a radius and a diameter of the circle.
Problem 2
Here is a circle with center H and some line segments and curves joining points on the circle.
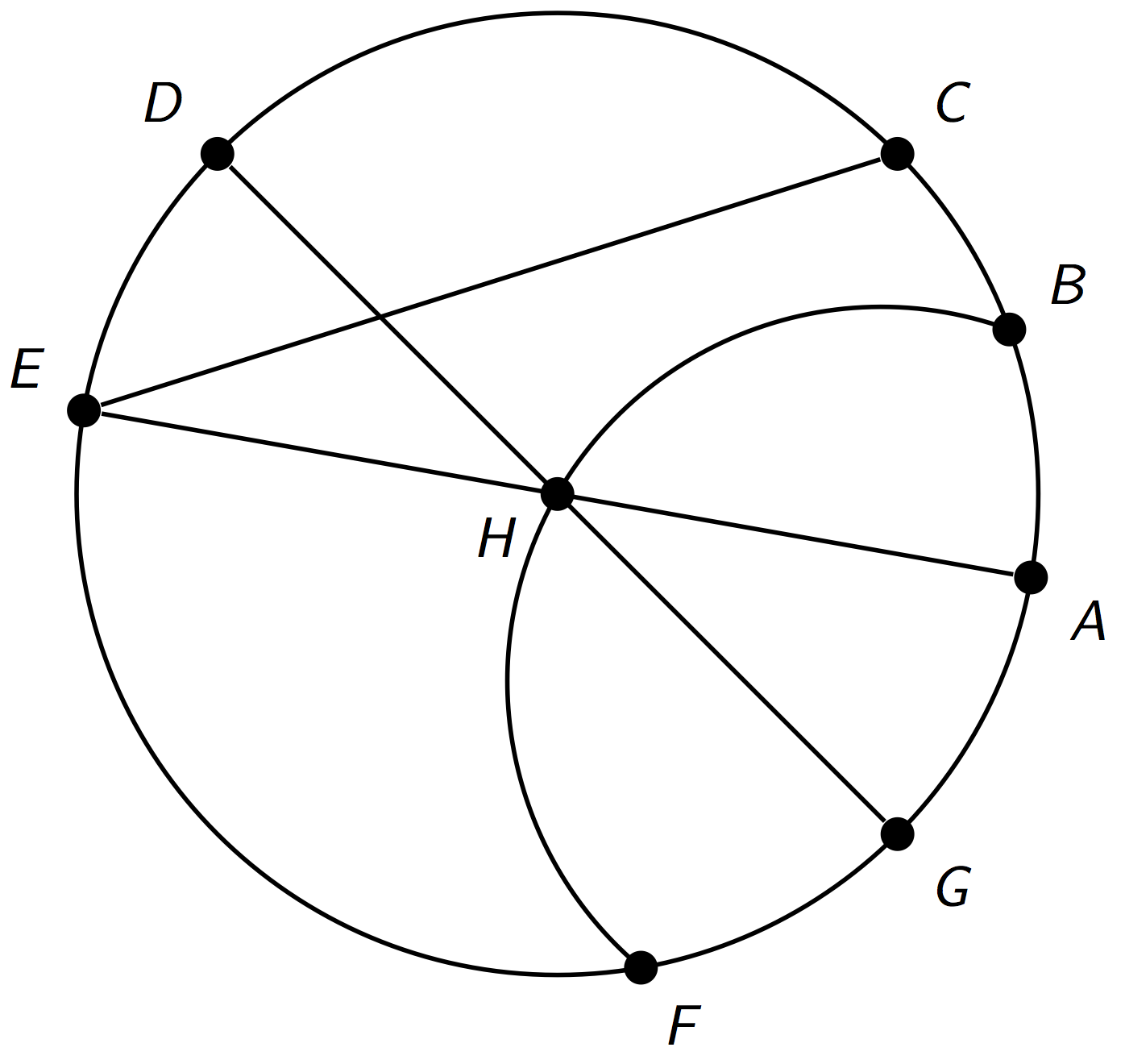
Identify examples of the following. Explain your reasoning.
-
Diameter
-
Radius
Problem 3
Lin measured the diameter of a circle in two different directions. Measuring vertically, she got 3.5 cm, and measuring horizontally, she got 3.6 cm. Explain some possible reasons why these measurements differ.
Problem 4 (from Unit 2, Lesson 1)
A small, test batch of lemonade used \frac{1}{4} cup of sugar added to 1 cup of water and \frac{1}{4} cup of lemon juice. After confirming it tasted good, a larger batch is going to be made with the same ratios using 10 cups of water. How much sugar should be added so that the large batch tastes the same as the test batch?
Problem 5 (from Unit 2, Lesson 13)
The graph of a proportional relationship contains the point with coordinates (3, 12). What is the constant of proportionality of the relationship?
Lesson 3
Problem 1
Diego measured the diameter and circumference of several circular objects and recorded his measurements in the table.
| object | diameter (cm) | circumference (cm) |
|---|---|---|
| half dollar coin | 3 | 10 |
| flying disc | 23 | 28 |
| jar lid | 8 | 25 |
| flower pot | 15 | 48 |
One of his measurements is inaccurate. Which measurement is it? Explain how you know.
Problem 2
Complete the table. Use one of the approximate values for \pi discussed in class (for example 3.14, \frac{22}{7}, 3.1416). Explain or show your reasoning.
| object | diameter | circumference |
|---|---|---|
| hula hoop | 35 in | |
| circular pond | 556 ft | |
| magnifying glass | 5.2 cm | |
| car tire | 71.6 in |
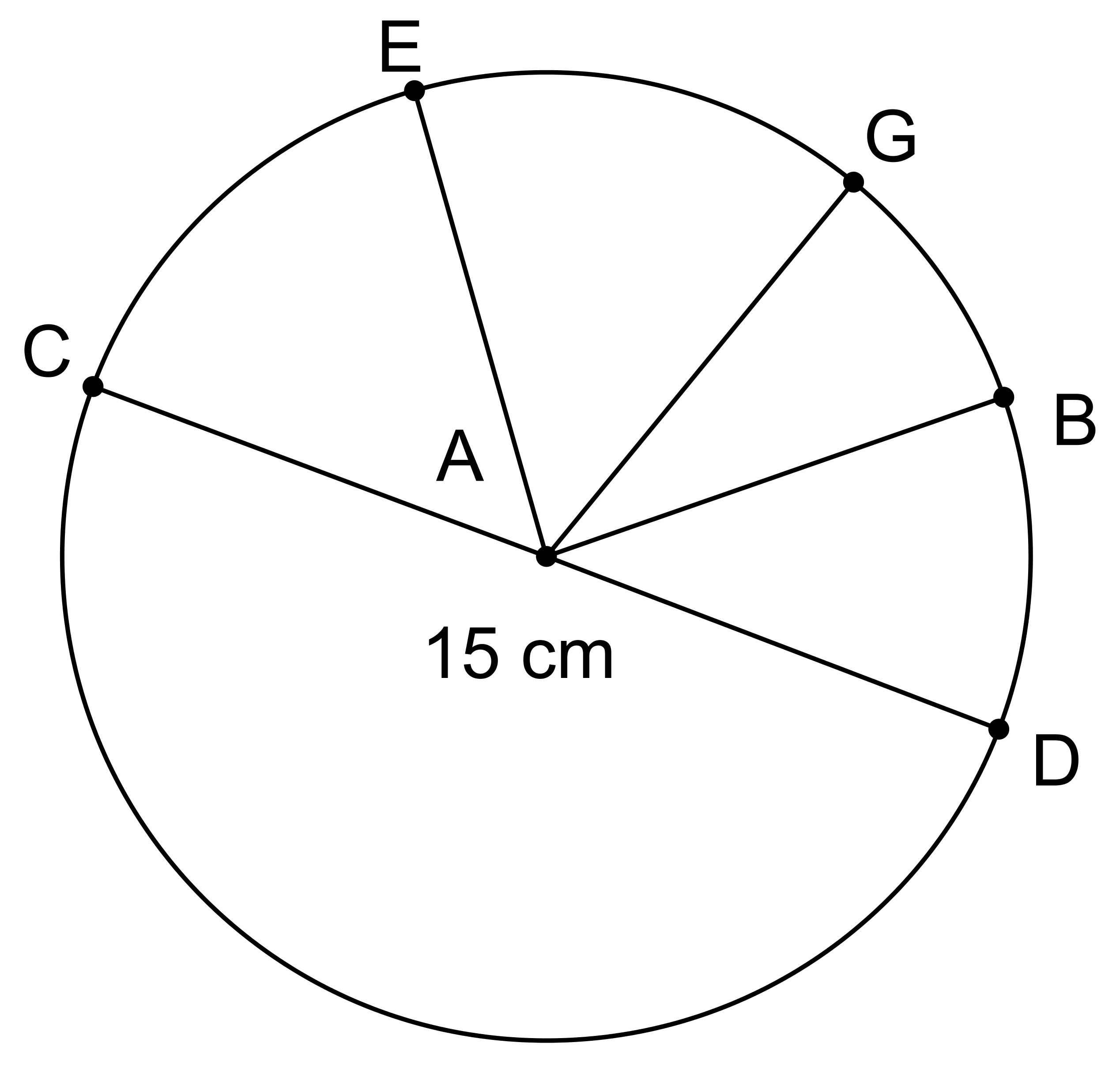
Problem 3 (from Unit 3, Lesson 2)
- Name a segment that is a radius. How long is it?
- Name a segment that is a diameter. How long is it?
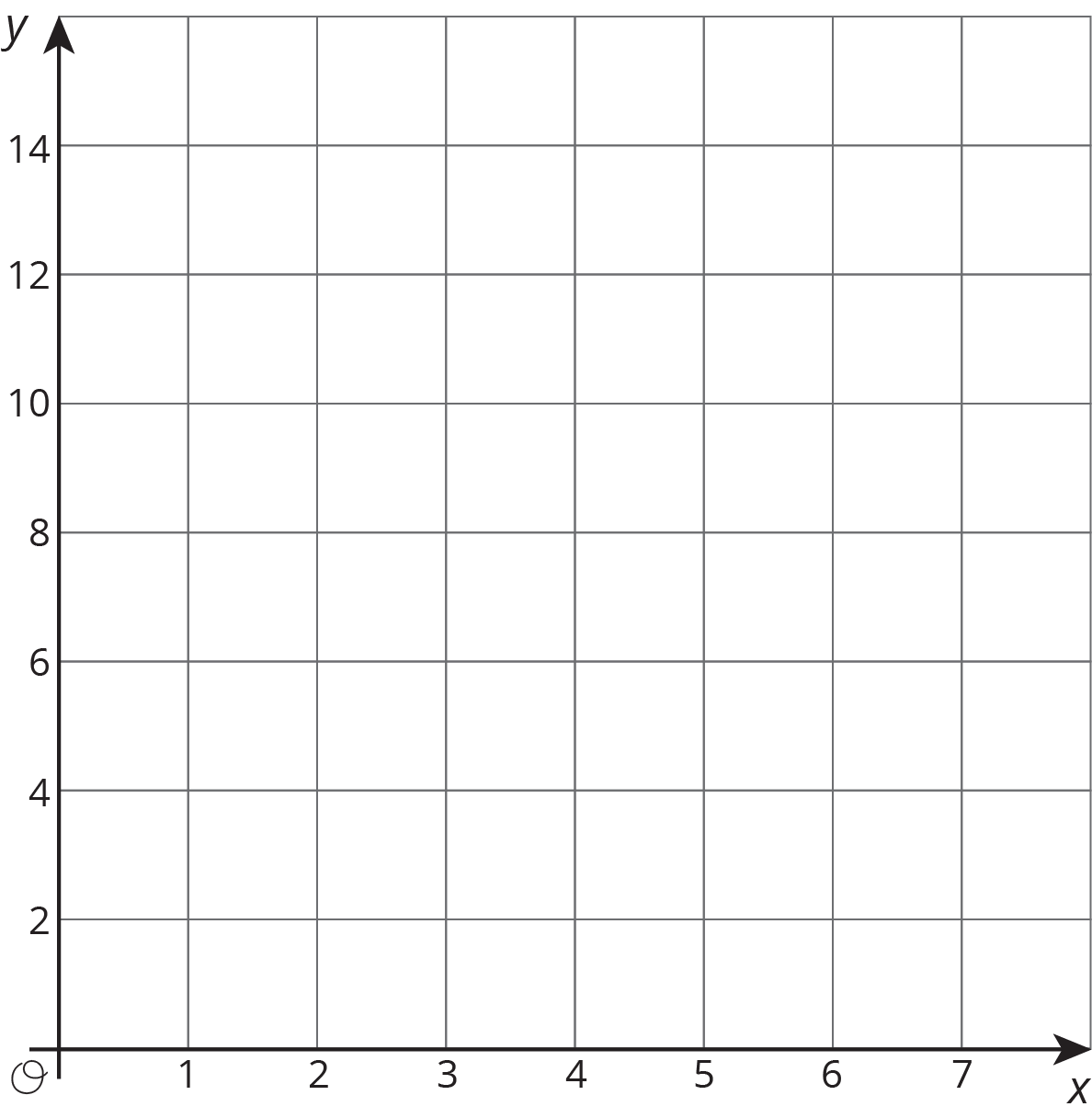
Problem 4 (from Unit 2, Lesson 10)
- Consider the equation y=1.5x +2. Find four pairs of x and y values that make the equation true. Plot the points (x, y) on the coordinate plane.
- Based on the graph, can this be a proportional relationship? Why or why not?
Lesson 4
Problem 1
Here is a picture of a Ferris wheel. It has a diameter of 80 meters.

-
On the picture, draw and label a diameter.
-
How far does a rider travel in one complete rotation around the Ferris wheel?
Problem 2
Identify each measurement as the diameter, radius, or circumference of the circular object. Then, estimate the other two measurements for the circle.
-
The length of the minute hand on a clock is 5 in.
-
The distance across a sink drain is 3.8 cm.
-
The tires on a mining truck are 14 ft tall.
-
The fence around a circular pool is 75 ft long.
-
The distance from the tip of a slice of pizza to the crust is 7 in.
-
Breaking a cookie in half creates a straight side 10 cm long.
-
The length of the metal rim around a glass lens is 190 mm.
-
From the center to the edge of a DVD measures 60 mm.
Problem 3
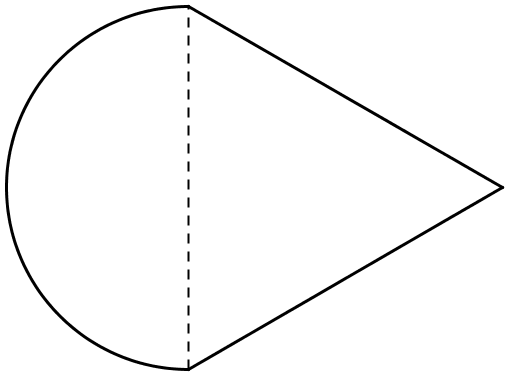
A half circle is joined to an equilateral triangle with side lengths of 12 units. What is the perimeter of the resulting shape?
Problem 4
Circle A has a diameter of 1 foot. Circle B has a circumference of 1 meter. Which circle is bigger? Explain your reasoning. (1 inch = 2.54 centimeters)
Problem 5 (from Unit 3, Lesson 3)
The circumference of Tyler's bike tire is 72 inches. What is the diameter of the tire?
Lesson 5
Problem 1
The diameter of a bike wheel is 27 inches. If the wheel makes 15 complete rotations, how far does the bike travel?
Problem 2
The wheels on Kiran's bike are 64 inches in circumference. How many times do the wheels rotate if Kiran rides 300 yards?
Problem 3 (from Unit 3, Lesson 4)
The numbers are measurements of radius, diameter, and circumference of circles A and B. Circle A is smaller than circle B. Which number belongs to which quantity? 2.5, 5, 7.6, 15.2, 15.7, 47.7
Problem 4 (from Unit 3, Lesson 3)
Circle A has circumference 2\frac23 m. Circle B has a diameter that is 1\frac12 times as long as Circle A’s diameter. What is the circumference of Circle B?
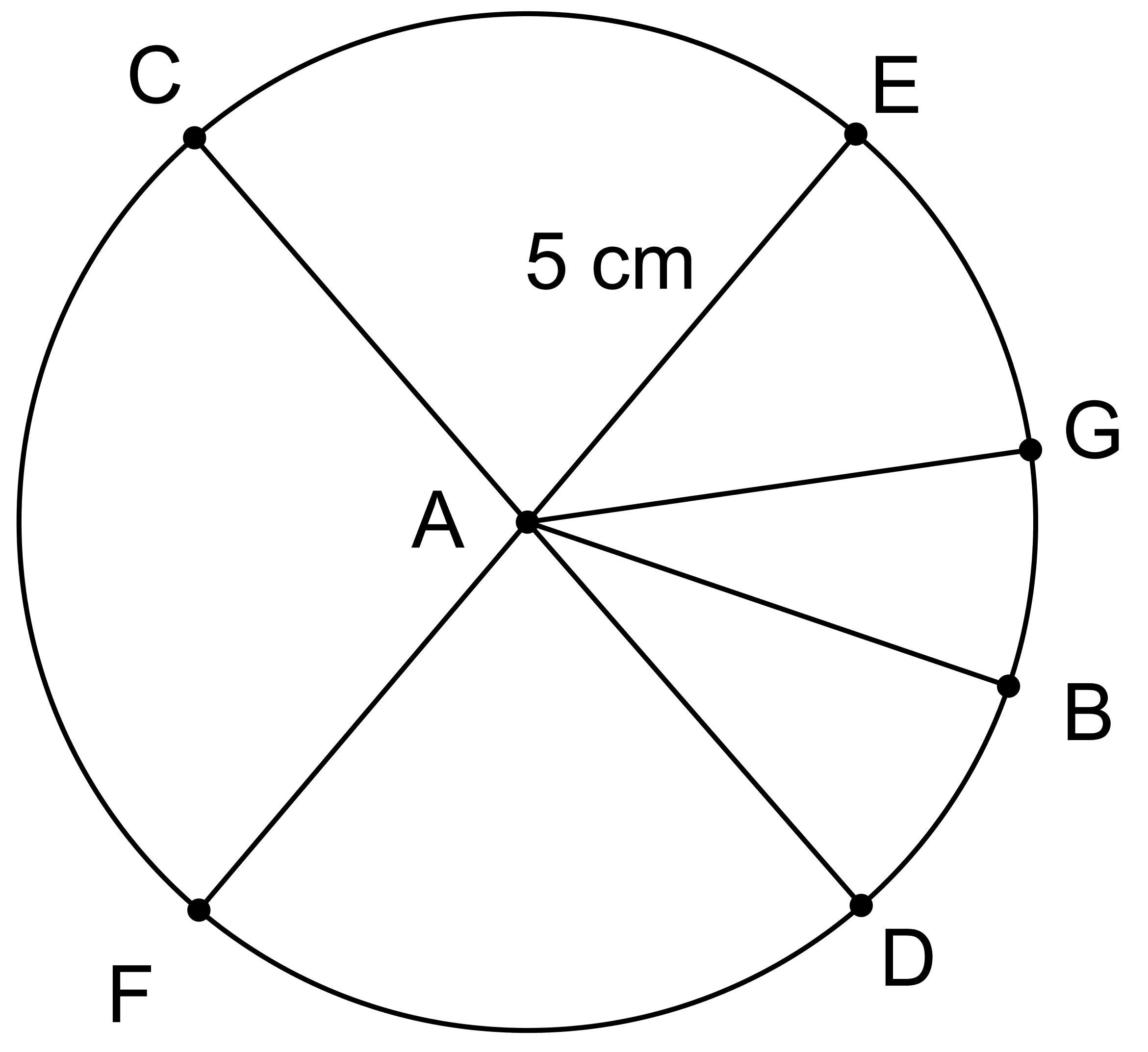
Problem 5 (from Unit 3, Lesson 2)
The length of segment AE is 5 centimeters.
- What is the length of segment CD?
- What is the length of segment AB?
- Name a segment that has the same length as segment AB.
Lesson 6
Problem 1
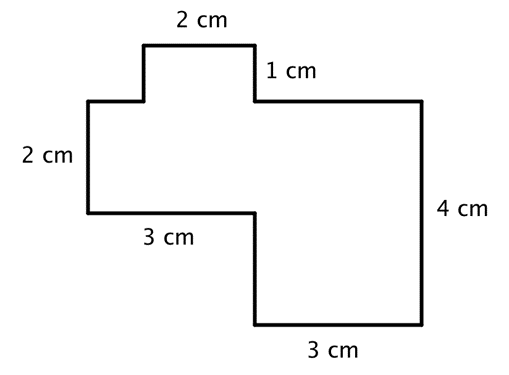
Find the area of the polygon.
Problem 2
- Draw polygons on the map that could be used to approximate the area of Virginia.
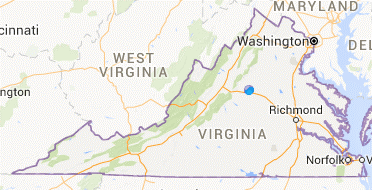
- Which measurements would you need to know in order to calculate an approximation of the area of Virginia? Label the sides of the polygons whose measurements you would need. (Note: You aren’t being asked to calculate anything.)
Problem 3 (from Unit 3, Lesson 5)
Jada’s bike wheels have a diameter of 20 inches. How far does she travel if the wheels rotate 37 times?
Problem 4 (from Unit 3, Lesson 4)
The radius of the earth is approximately 6400 km. The equator is the circle around the earth dividing it into the northern and southern hemisphere. (The center of the earth is also the center of the equator.) What is the length of the equator?
Problem 5 (from Unit 2, Lesson 1)
Here are several recipes for sparkling lemonade. For each recipe describe how many tablespoons of lemonade mix it takes per cup of sparkling water.
Recipe 1: 4 tablespoons lemonade mix and 12 cups of sparkling water
Recipe 2: 4 tablespoons of lemonade mix and 6 cups of sparkling water
Recipe 3: 3 tablespoons of lemonade mix and 5 cups of sparkling water
Recipe 4: \frac12 tablespoon os lemonade mix and \frac34 cups of sparkling water
Lesson 7
Problem 1
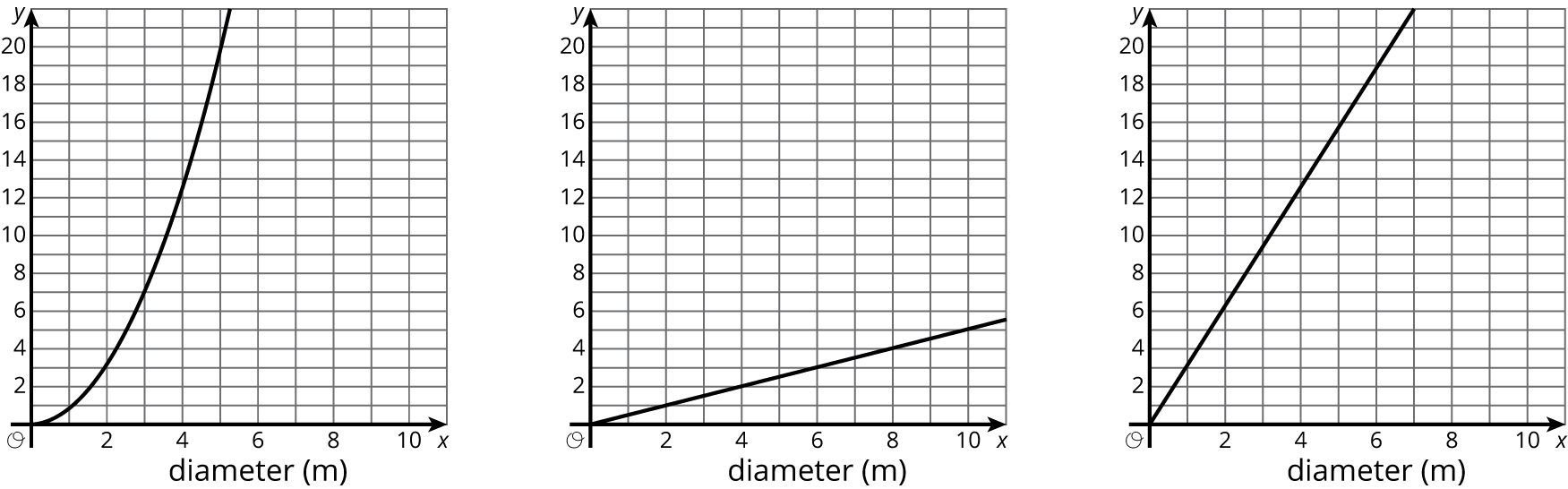
The x-axis of each graph has the diameter of a circle in meters. Label the y-axis on each graph with the appropriate measurement of a circle: radius (m), circumference (m), or area (m2).
Problem 2
-
Here is a picture of two squares and a circle. Use the picture to explain why the area of this circle is more than 2 square units but less than 4 square units.
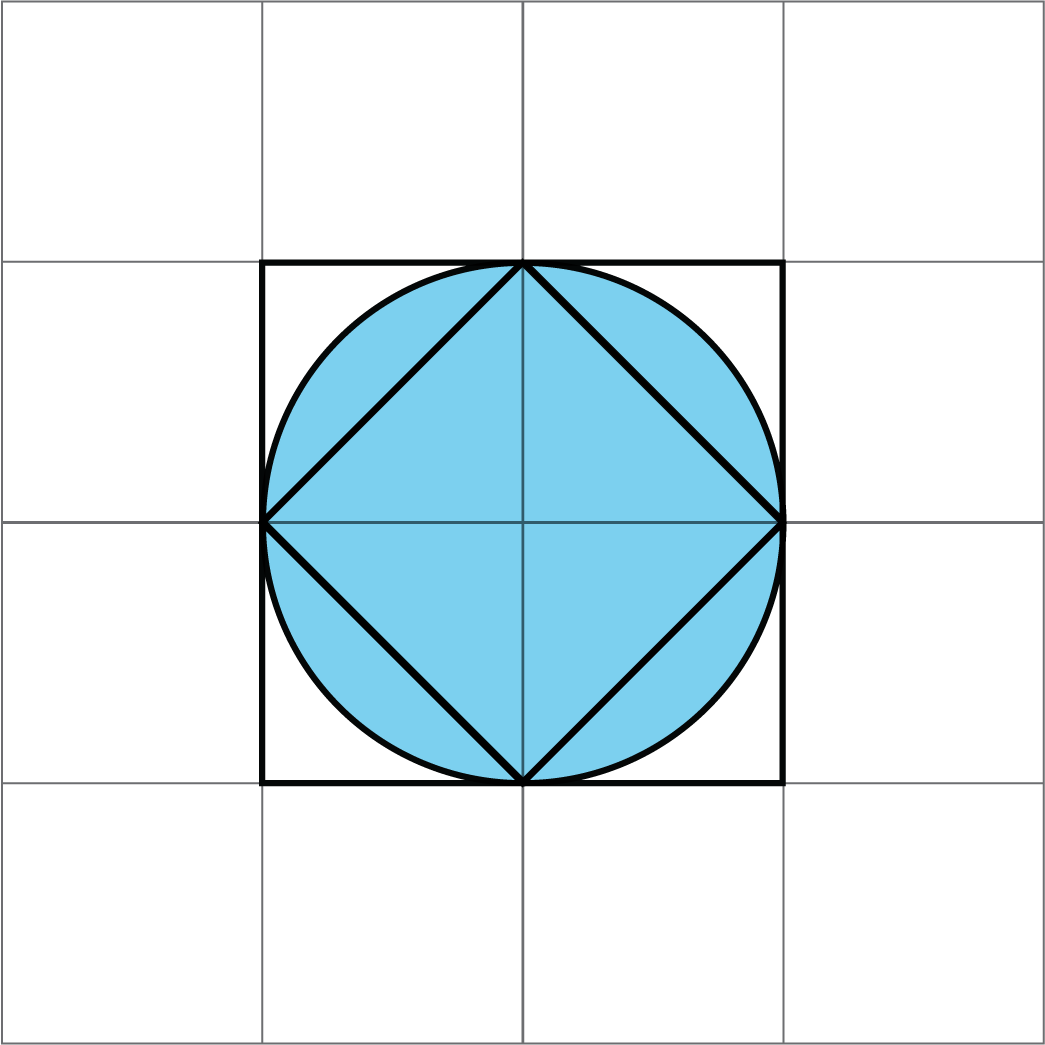
-
Here is another picture of two squares and a circle. Use the picture to explain why the area of this circle is more than 18 square units and less than 36 square units.
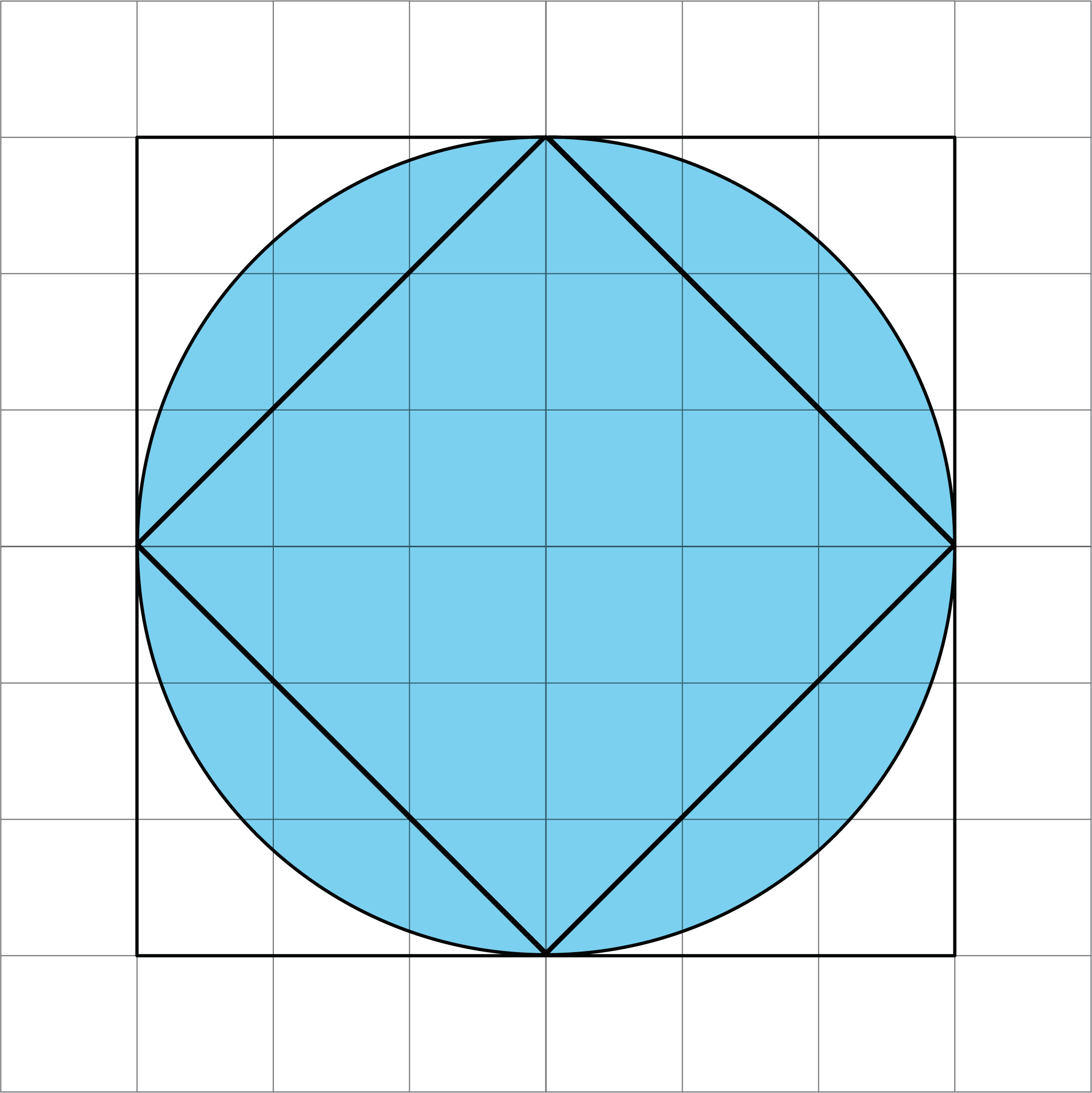
Problem 3
Circle A has area 500 in2. The diameter of circle B is three times the diameter of circle A. Estimate the area of circle B.
Problem 4 (from Unit 3, Lesson 5)
Lin’s bike travels 100 meters when her wheels rotate 55 times. What is the circumference of her wheels?
Problem 5 (from Unit 3, Lesson 3)
Find the circumference of this circle.

Problem 6 (from Unit 3, Lesson 3)
Priya drew a circle whose circumference is 25 cm. Clare drew a circle whose diameter is 3 times the diameter of Priya’s circle. What is the circumference of Clare’s circle?
Lesson 8
Problem 1
The picture shows a circle divided into 8 equal wedges which are rearranged.
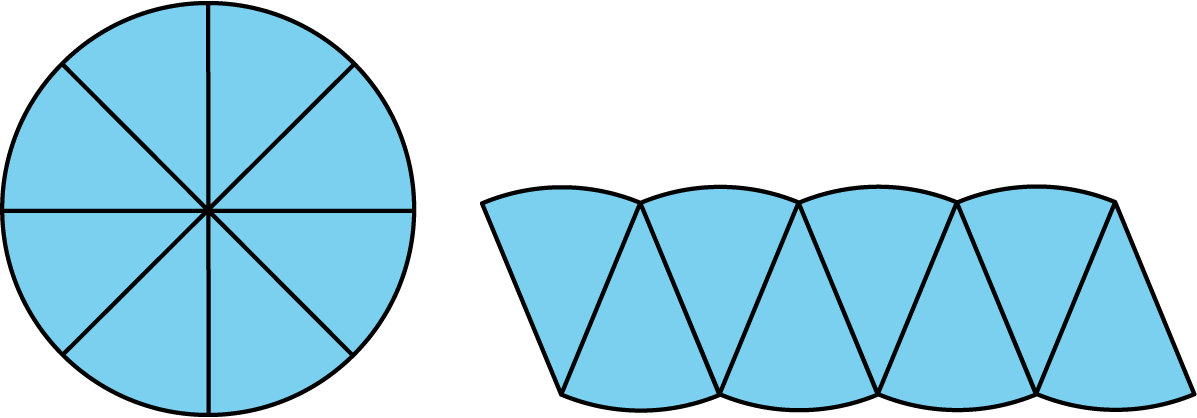
The radius of the circle is r and its circumference is 2\pi r. How does the picture help to explain why the area of the circle is \pi r^2?
Problem 2
A circle’s circumference is approximately 76 cm. Estimate the radius, diameter, and area of the circle.
Problem 3
Jada paints a circular table that has a diameter of 37 inches. What is the area of the table?
Problem 4 (from Unit 3, Lesson 4)
The Carousel on the National Mall has 4 rings of horses. Kiran is riding on the inner ring, which has a radius of 9 feet. Mai is riding on the outer ring, which is 8 feet farther out from the center than the inner ring is.
-
In one rotation of the carousel, how much farther does Mai travel than Kiran?
-
One rotation of the carousel takes 12 seconds. How much faster does Mai travel than Kiran?
Problem 5 (from Unit 3, Lesson 5)
Here are the diameters of four coins:
| coin | penny | nickel | dime | quarter |
|---|---|---|---|---|
| diameter | 1.9 cm | 2.1 cm | 1.8 cm | 2.4 cm |
- A coin rolls a distance of 33 cm in 5 rotations. Which coin is it?
- A quarter makes 8 rotations. How far did it roll?
- A dime rolls 41.8 cm. How many rotations did it make?
Lesson 9
Problem 1
A circle with a 12 inch diameter is folded in half and then folded in half again. What is the area of the resulting shape?
Problem 2
Find the area of the shaded region. Express your answer in terms of \pi.
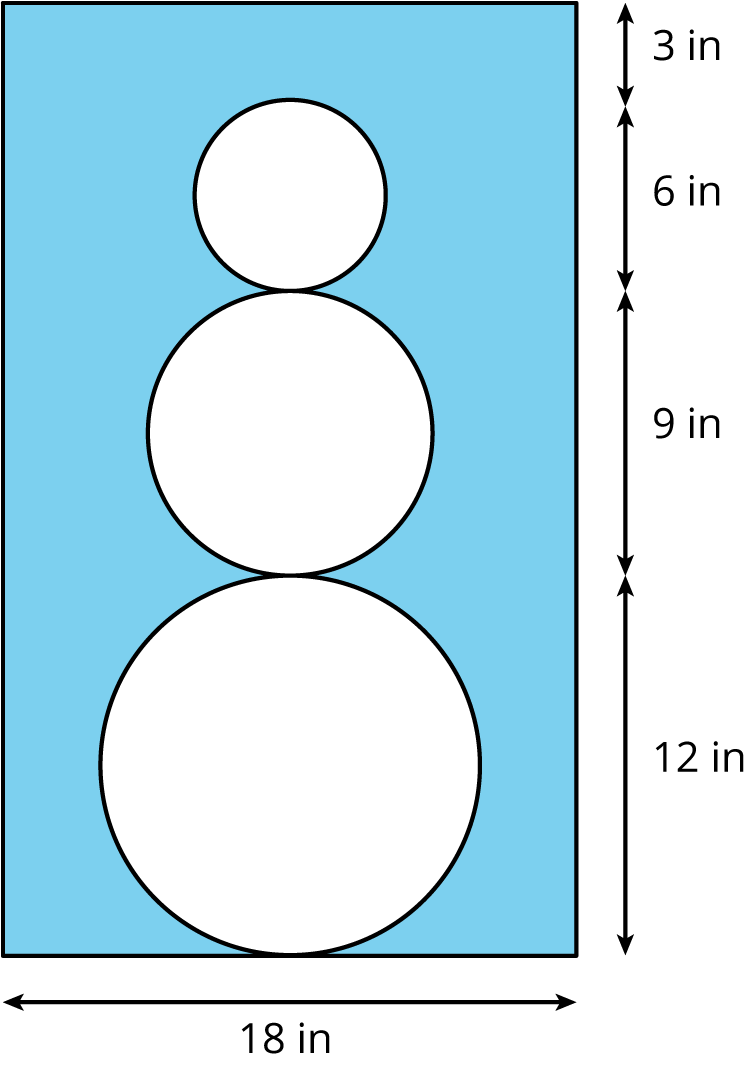
Problem 3 (from Unit 3, Lesson 8)
The face of a clock has a circumference of 63 in. What is the area of the face of the clock?
Problem 4 (from Unit 3, Lesson 7)
Which of these pairs of quantities are proportional to each other? For the quantities that are proportional, what is the constant of proportionality?
- Radius and diameter of a circle
- Radius and circumference of a circle
- Radius and area of a circle
- Diameter and circumference of a circle
- Diameter and area of a circle
Problem 5 (from Unit 3, Lesson 6)
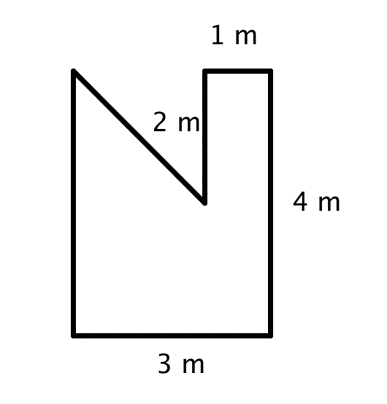
Find the area of this shape in two different ways.
Problem 6 (from Unit 2, Lesson 5)
Elena and Jada both read at a constant rate, but Elena reads more slowly. For every 4 pages that Elena can read, Jada can read 5.
- Complete the table.
row 1 pages read
by Elenapages read
by Jadarow 2 4 5 row 3 1 row 4 9 row 5 s row 6 15 row 7 j - Here is an equation for the table: j = 1.25e. What does the 1.25 mean?
- Write an equation for this relationship that starts e = \text{...}
Lesson 10
Problem 1
For each problem, decide whether the circumference of the circle or the area of the circle is most useful for finding a solution. Explain your reasoning.
-
A car’s wheels spin at 1000 revolutions per minute. The diameter of the wheels is 23 inches. You want to know how fast the car is travelling.
-
A circular kitchen table has a diameter of 60 inches. You want to know how much fabric is needed to cover the table top.
-
A circular puzzle is 20 inches in diameter. All of the pieces are about the same size. You want to know about how many pieces there are in the puzzle.
-
You want to know about how long it takes to walk around a circular pond.
Problem 2
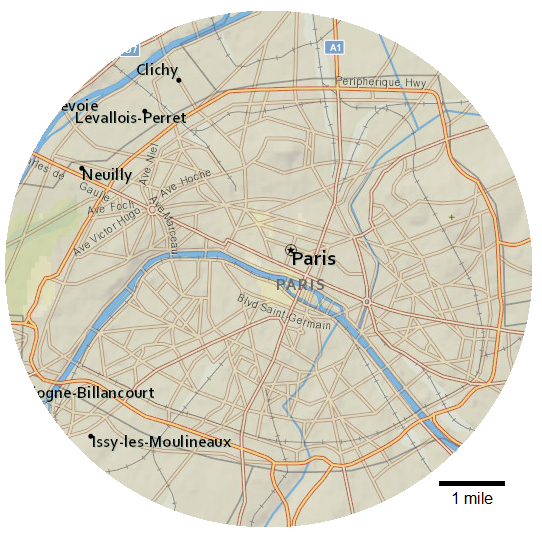
The city of Paris, France is completely contained within an almost circular road that goes around the edge. Use the map with its scale to:
-
Estimate the circumference of Paris.
-
Estimate the area of Paris.
Problem 3
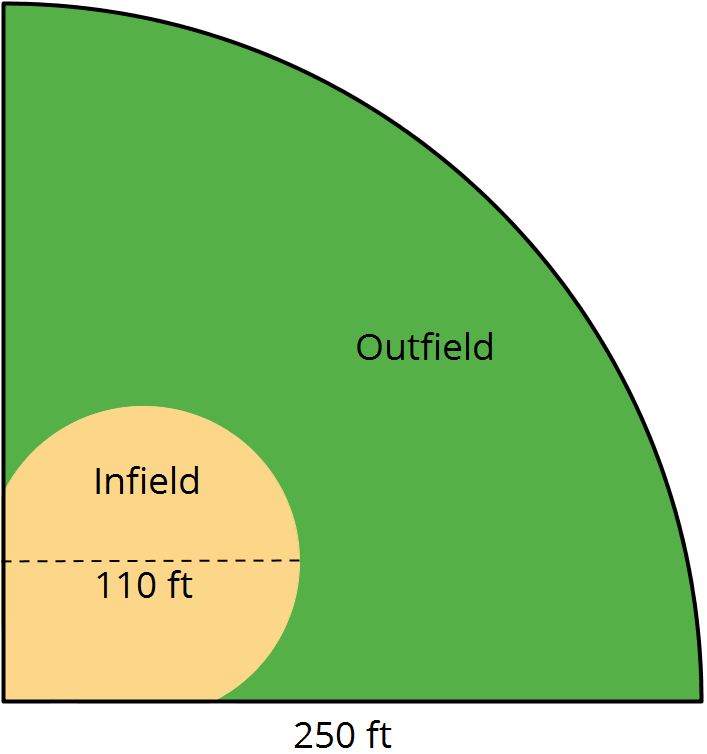
Here is a diagram of a softball field:
-
About how long is the fence around the field?
-
About how big is the outfield?
Problem 4 (from Unit 2, Lesson 5)
While in math class, Priya and Kiran come up with two ways of thinking about the proportional relationship shown in the table.
| row 1 | x | y |
|---|---|---|
| row 2 | 2 | ? |
| row 3 | 5 | 1750 |
Both students agree that they can solve the equation 5k = 1750 to find the constant of proportionality.
- Priya says, “I can solve this equation by dividing 1750 by 5.”
- Kiran says, “I can solve this equation by multiplying 1750 by \frac15.”
- What value of k would each student get using their own method?
- How are Priya and Kiran's approaches related?
- Explain how each student might approach solving the equation \frac23 k=50.
Lesson 11
No practice problems for this lesson.