Lesson 8: Percent Increase and Decrease with Equations

Let’s use equations to represent increases and decreases.

How do you get from one number to the next using multiplication or division?

From 100 to 106
From 100 to 90

From 90 to 100
From 106 to 100

Money in a particular savings account increases by about 6% after a year. How much money will be in the account after one year if the initial amount is $100? $50? 200? 125? $x$ dollars? If you get stuck, consider using diagrams or a table to organize your work.
The value of a new car decreases by about 15% in the first year. How much will a car be worth after one year if its initial value was $1,000? 5,000? 5,020? $x$ dollars? If you get stuck, consider using diagrams or a table to organize your work.

Match an equation to each of these situations. Be prepared to share your reasoning.

The water level in a reservoir is now 52 meters. If this was a 23% increase, what was the initial depth?
The snow is now 52 inches deep. If this was a 77% decrease, what was the initial depth?

$0.23x = 52$

$0.77x = 52$

$1.23x = 52$

$1.77x = 52$

Are You Ready For More?

An astronaut was exploring the moon of a distant planet, and found some glowing goo at the bottom of a very deep crater. She brought a 10-gram sample of the goo to her laboratory. She found that when the goo was exposed to light, the total amount of goo increased by 100% every hour.

How much goo will she have after 1 hour? After 2 hours? After 3 hours? After $n$ hours?
When she put the goo in the dark, it shrank by 75% every hour. How many hours will it take for the goo that was exposed to light for $n$ hours to return to the original size?

The gas tank in dad’s car holds 12 gallons. The gas tank in mom’s truck holds 50% more than that. How much gas does the truck’s tank hold?

Explain why this situation can be represented by the equation $(1.5) \boldcdot 12 = t$ . Make sure that you explain what $t$ represents.
Write an equation to represent each of the following situations.
1. A movie theater decreased the size of its popcorn bags by 20%. If the old bags held 15 cups of popcorn, how much do the new bags hold?
2. After a 25% discount, the price of a T-shirt was $12. What was the price before the discount?
3. Compared to last year, the population of Boom Town has increased by 25%.The population is now 6,600. What was the population last year?

Summary

We can use equations to express percent increase and percent decrease. For example, if $y$ is 15% more than $x$ ,

we can represent this using any of these equations:

$y = x + 0.15x$

$y = (1 + 0.15)x$

$y = 1.15x$

So if someone makes an investment of $x$ dollars, and its value increases by 15% to 1250, then we can write and solve the equation $1.15x =1250$ to find the value of the initial investment.

Here is another example: if $a$ is 7% less than $b$ ,

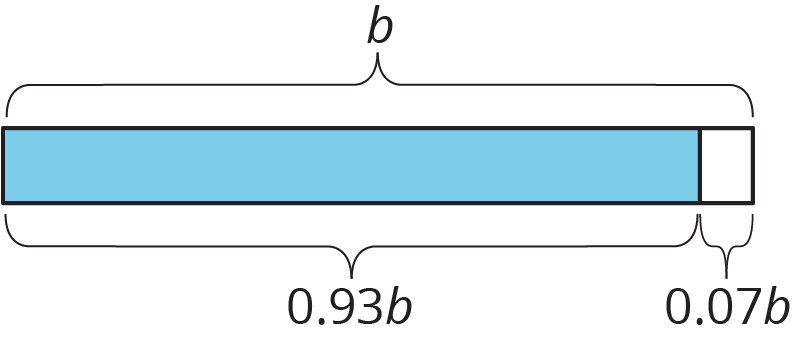
we can represent this using any of these equations:

$a = b - 0.07b$

$a = (1-0.07)b$

$a = 0.93b$

So if the amount of water in a tank decreased 7% from its starting value of $b$ to its ending value of 348 gallons, then you can write $0.93b = 348$ .

Often, an equation is the most efficient way to solve a problem involving percent increase or percent decrease.

Lesson 8: Percent Increase and Decrease with Equations

8.1: From 100 to 106

8.2: Interest and Depreciation

8.3: Matching Equations

Are You Ready For More?

8.4: Representing Percent Increase and Decrease: Equations

Summary

Practice Problems ▶