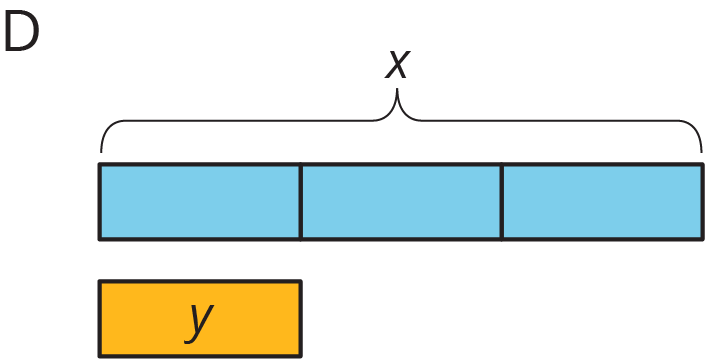
4.1: Notice and Wonder: Tape Diagrams
What do you notice? What do you wonder?
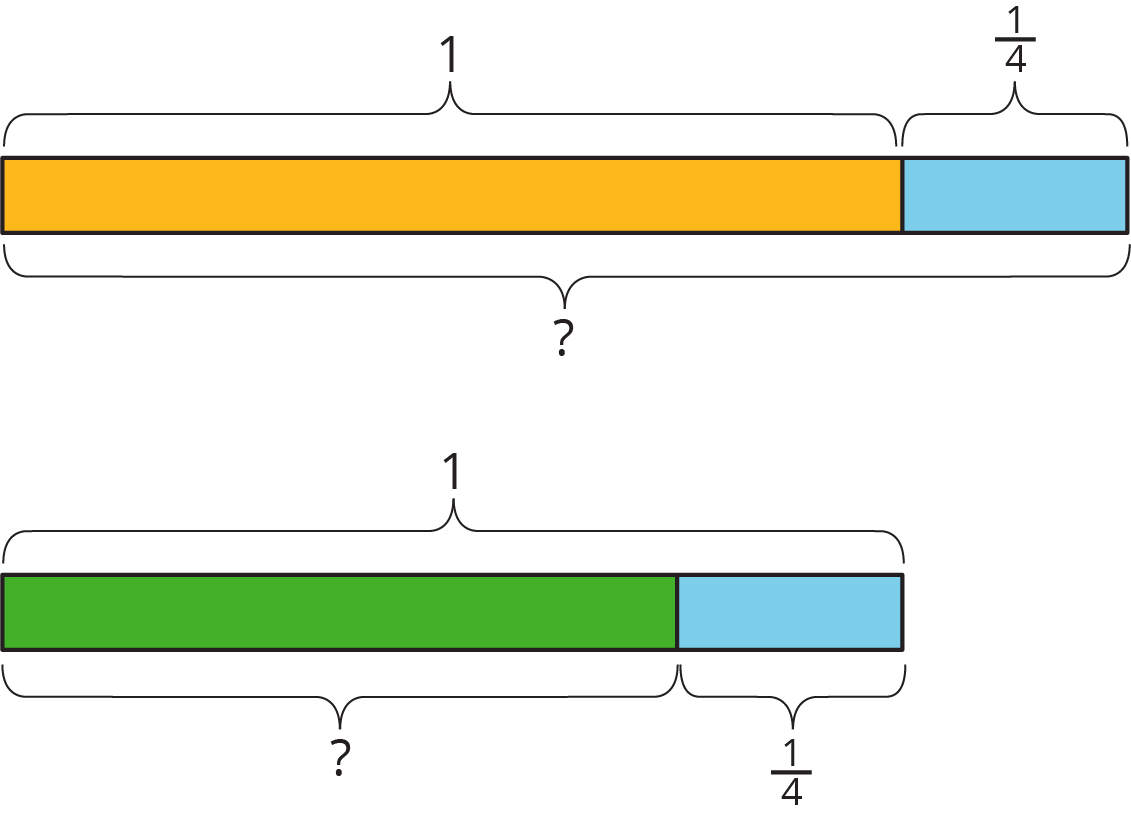
Let’s use fractions to describe increases and decreases.
What do you notice? What do you wonder?

Complete the table to show the total distance walked in each case.
| initial distance | total distance | |
|---|---|---|
| row 1 | 10 | |
| row 2 | 3 | |
| row 3 | 4.5 | |
| row 4 | 1 | |
| row 5 | x |
Two students each wrote an equation to represent the relationship between the initial distance walked (x) and the total distance walked (y).
Do you agree with either of them? Explain your reasoning.
Zeno jumped 8 meters. Then he jumped half as far again (4 meters). Then he jumped half as far again (2 meters). So after 3 jumps, he was 8 + 4 + 2 = 14 meters from his starting place.
Match each situation with a diagram. A diagram may not have a match.
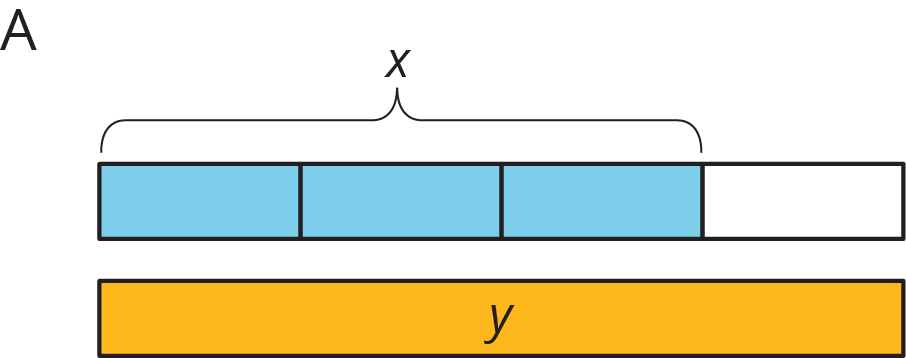
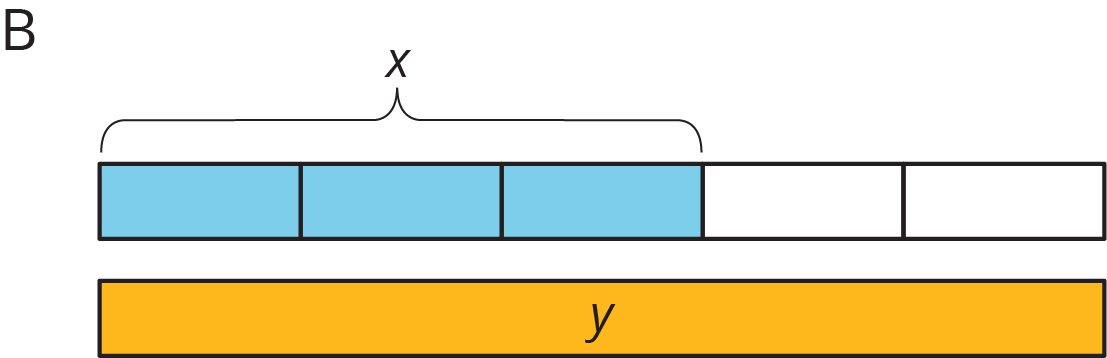
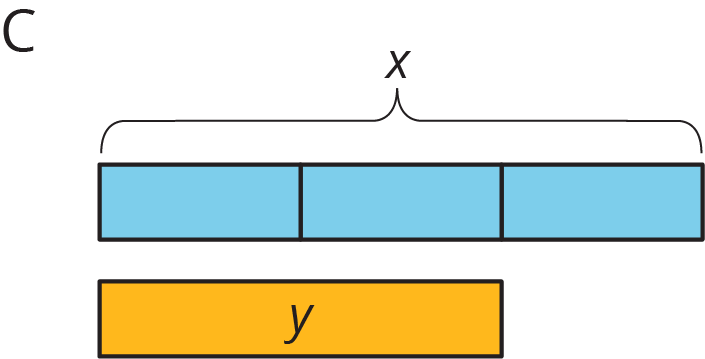
Your teacher will give you a set of cards that have proportional relationships represented 3 different ways: as descriptions, equations, and tables. Mix up the cards and place them all face-up.
Using the distributive property provides a shortcut for calculating the final amount in situations that involve adding or subtracting a fraction of the original amount.
For example, one day Clare runs 4 miles. The next day, she plans to run that same distance plus half as much again. How far does she plan to run the next day?
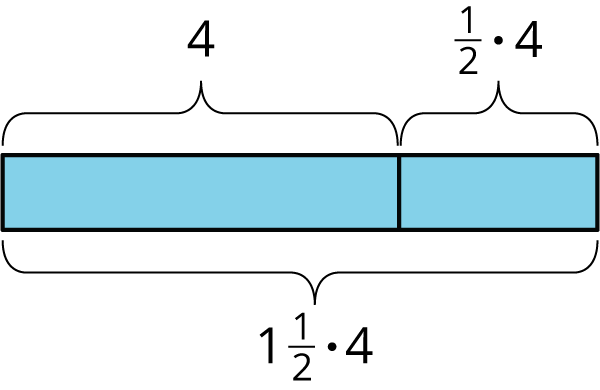
Tomorrow she will run 4 miles plus \frac12 of 4 miles. We can use the distributive property to find this in one step: 1 \boldcdot 4 + \frac{1}{2} \boldcdot 4 = \left(1 + \frac{1}{2}\right) \boldcdot 4
Clare plans to run 1\frac12\boldcdot 4, or 6 miles.
This works when we decrease by a fraction, too. If Tyler spent x dollars on a new shirt, and Noah spent \frac{1}{3} less than Tyler, then Noah spent \frac{2}{3}x dollars since x-\frac{1}{3}x=\frac{2}{3}x.