When we are measuring a length using a ruler or measuring tape, we can get a measurement that is different from the actual length. This could be because we positioned the ruler incorrectly, or it could be because the ruler is not very precise. There is always at least a small difference between the actual length and a measured length, even if it is a microscopic difference!
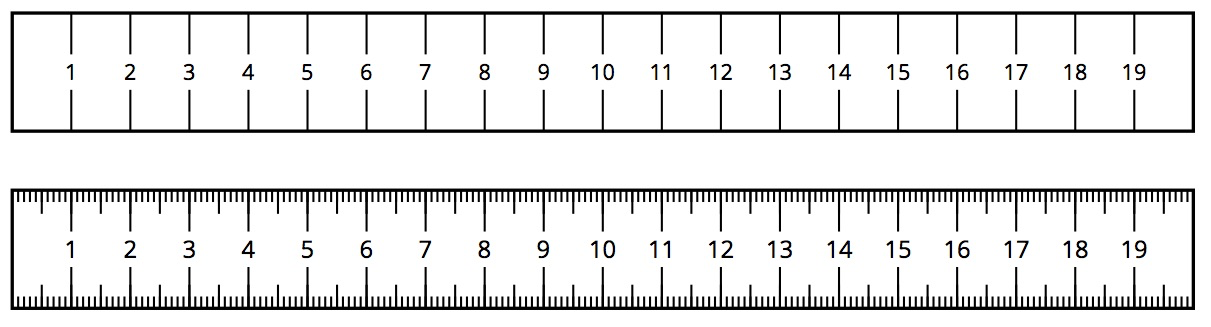
Here are two rulers with different markings.
The second ruler is marked in millimeters, so it is easier to get a measurement to the nearest tenth of a centimeter with this ruler than with the first. For example, a line that is actually 6.2 cm long might be measured to be 6 cm long by the first ruler, because we measure to the nearest centimeter.
The measurement error is the positive difference between the measurement and the actual value. Measurement error is often expressed as a percentage of the actual value. We always use a positive number to express measurement error and, when appropriate, use words to describe whether the measurement is greater than or less than the actual value.
For example, if we get 6 cm when we measure a line that is actually 6.2 cm long, then the measurement error is 0.2 cm, or about 3.2%, because 0.2 \div 6.2 \approx 0.032.