Any cross section of a prism that is parallel to the base will be identical to the base. This means we can slice prisms up to help find their volume. For example, if we have a rectangular prism that is 3 units tall and has a base that is 4 units by 5 units, we can think of this as 3 layers, where each layer has $4\boldcdot 5$ cubic units.

That means the volume of the original rectangular prism is $3(4\boldcdot 5)$ cubic units.
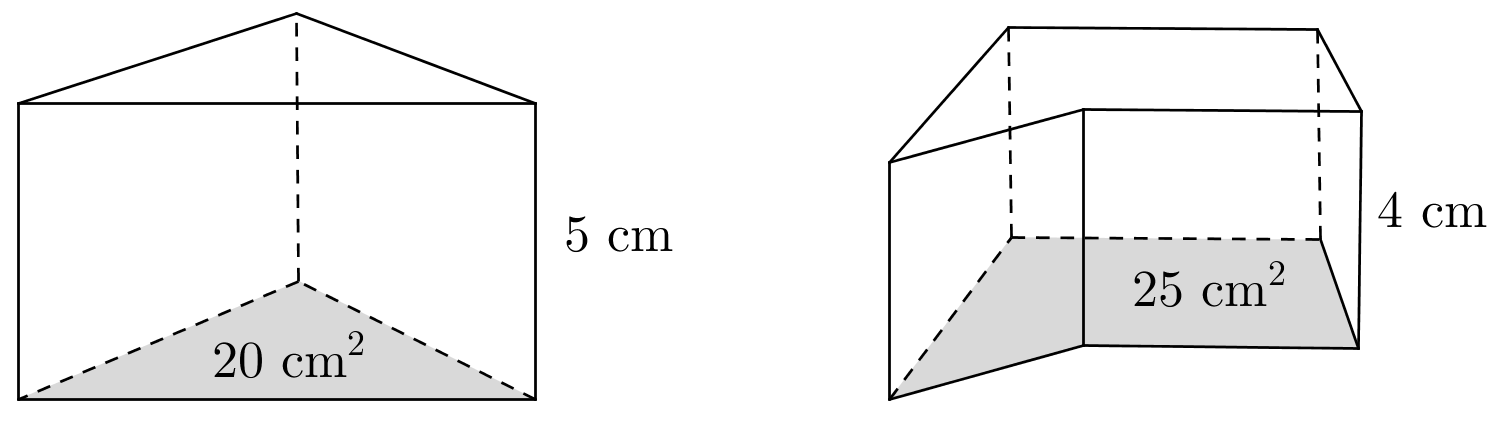
This works with any prism! If we have a prism with height 3 cm that has a base of area 20 cm2, then the volume is $3\boldcdot 20$ cm3 regardless of the shape of the base. In general, the volume of a prism with height $h$ and area $B$ is
$$V = B \boldcdot h$$
For example, these two prisms both have a volume of 100 cm3.