Lesson 8: Comparing Relationships with Equations

Let’s develop methods for deciding if a relationship is proportional.

8.1: Notice and Wonder: Patterns with Rectangles

Three rectangles on a coordinate grid. The dimensions are as follows: Top rectangle, length 3 units; width 1 unit. Middle rectangle, length 6 units; width 2 units. Bottom rectangle, length 9 units, width 3 units.
Do you see a pattern? What predictions can you make about future rectangles in the set if your pattern continues?

8.2: More Conversions

The other day you worked with converting meters, centimeters, and millimeters. Here are some more unit conversions.

  1. Use the equation F =\frac95 C + 32, where F represents degrees Fahrenheit and C represents degrees Celsius, to complete the table.
      temperature (^\circ\text{C}) temperature (^\circ\text{F})
    row 1 20  
    row 2 4  
    row 3 175  
  2. Use the equation c = 2.54n, where c represents the length in centimeters and n represents the length in inches, to complete the table.
      length (in) length (cm)
    row 1 10  
    row 2 8  
    row 3 3\frac12  
  3. Are these proportional relationships? Explain why or why not.

8.3: Total Edge Length, Surface Area, and Volume

Here are some cubes with different side lengths. Complete each table. Be prepared to explain your reasoning.

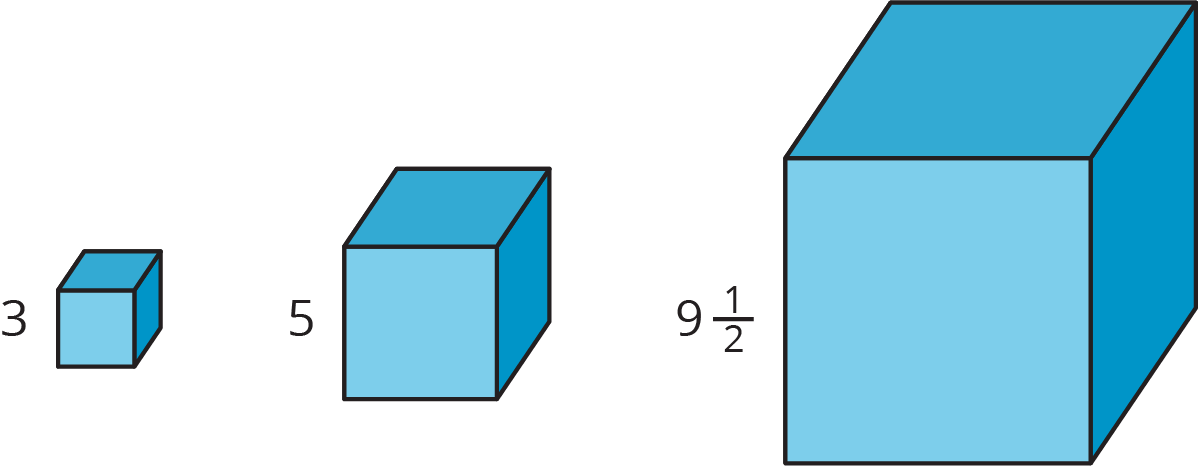
Three cubes of different sizes: first cube has side length 3, second cube side length 5, and thrid cube has side length 9 and 1/2
  1. How long is the total edge length of each cube?
row 1 side
length		 total
edge length
row 2 3  
row 3 5  
row 4 9\frac12  
row 4 s  
  1. What is the surface area of each cube?
row 1 side
length		 surface
area
row 2 3  
row 3 5  
row 4 9\frac12  
row 5 s  
  1. What is the volume of each cube?
row 1 side
length		 volume
row 2 3  
row 3 5  
row 4 9\frac12  
row 5 s  
  1. Which of these relationships is proportional? Explain how you know.

  2. Write equations for the total edge length E, total surface area A, and volume V of a cube with side length s.

8.4: All Kinds of Equations

Here are six different equations.

y = 4 + x

y = \frac{x}{4}

y = 4x

y = 4^{x}

y = \frac{4}{x}

y = x^{4}

  1. Predict which of these equations represent a proportional relationship.
  1. Complete each table using the equation that represents the relationship.
Six identical three column tables with 4 rows of data: The first column is labeled "x", the second column is labeled "y", and the third column is labeled "the fraction y over x". Row 1: x, 2. Row 2: x, 3. Row 3: x, 4. Row 4: x, 5. Each table has an equation above it, as follows: Table 1, Equation 1: y equals 4 + x; Table 2, Equation 2: y equals 4x; Table 3, Equation 3: y equals the fraction 4 over x; Table 4, Equation 4: y equals x the fraction x over 4; Table 5, Equation 5: y equals 4 to power x; Table 6, Equation 6: y equals x to the power 4;
  1. Do these results change your answer to the first question? Explain your reasoning.
  2. What do the equations of the proportional relationships have in common?

Summary

If two quantities are in a proportional relationship, then their quotient is always the same. This table represents different values of a and b, two quantities that are in a proportional relationship.

row 1 a b \frac{b}{a}
row 2 20 100 5
row 3 3 15 5
row 4 11 55 5
row 5 1 5 5

Notice that the quotient of b and a is always 5. To write this as an equation, we could say \frac{b}{a}=5. If this is true, then b=5a. (This doesn’t work if a=0, but it works otherwise.)

If quantity y is proportional to quantity x, we will always see this pattern: \frac{y}{x} will always have the same value. This value is the constant of proportionality, which we often refer to as k. We can represent this relationship with the equation \frac{y}{x} = k (as long as x is not 0) or y=kx.

Note that if an equation cannot be written in this form, then it does not represent a proportional relationship. 

Practice Problems ▶