If we want to build a polygon with two given side lengths that share a vertex, we can think of them as being connected by a hinge that can be opened or closed:
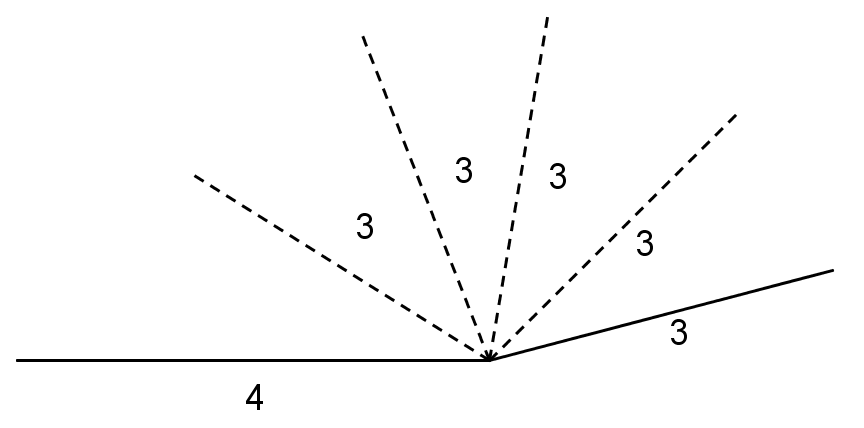 All of the possible positions of the endpoint of the moving side form a circle:
All of the possible positions of the endpoint of the moving side form a circle: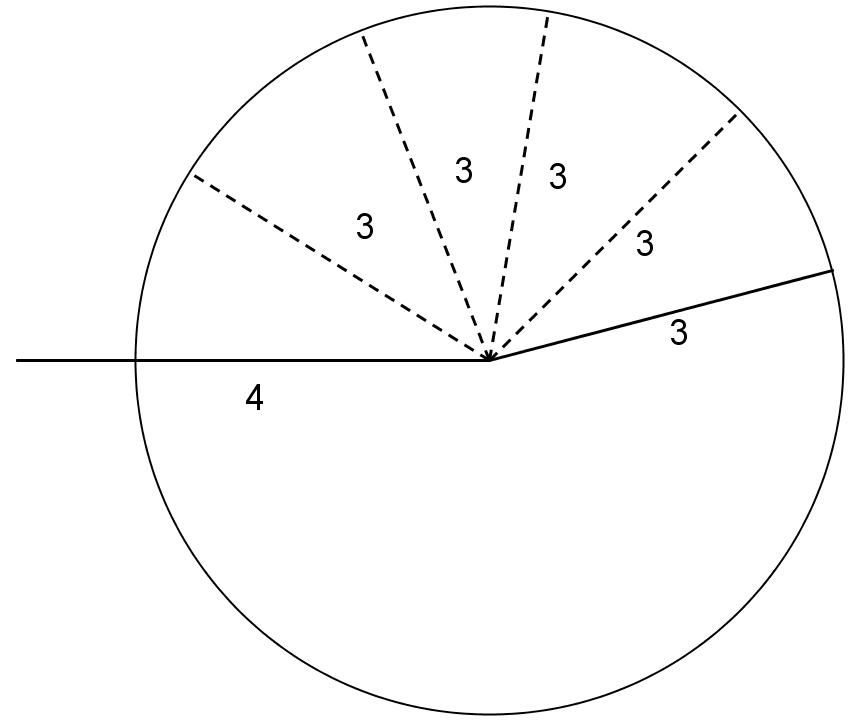
You may have noticed that sometimes it is not possible to build a polygon given a set of lengths. For example, if we have one really, really long segment and a bunch of short segments, we may not be able to connect them all up. Here's what happens if you try to make a triangle with side lengths 21, 4, and 2: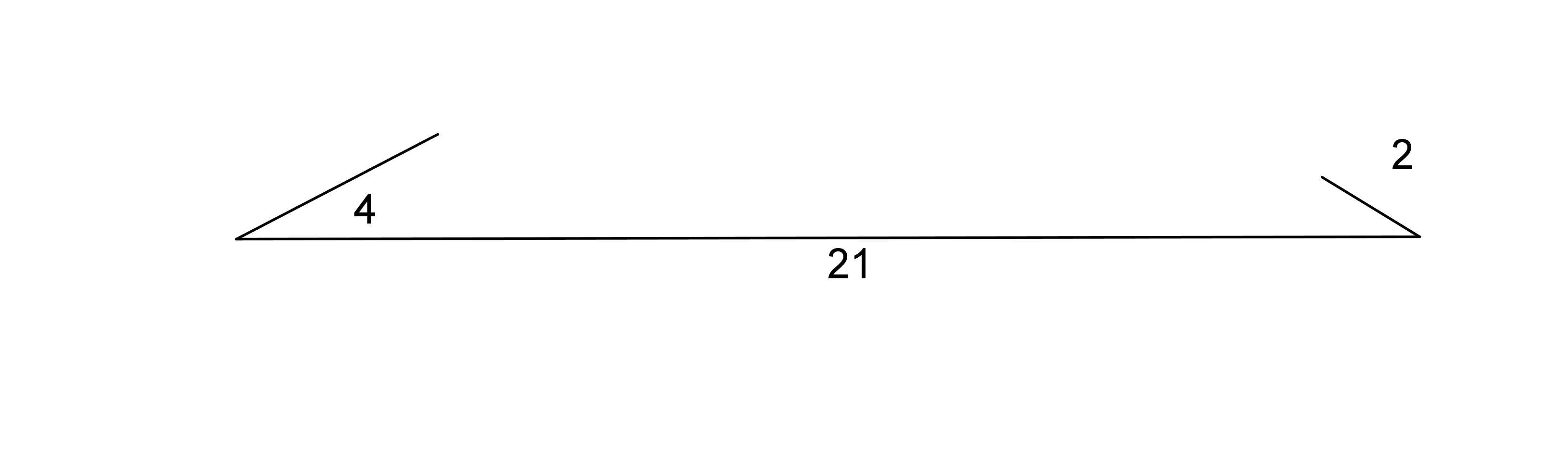
The short sides don't seem like they can meet up because they are too far away from each other.
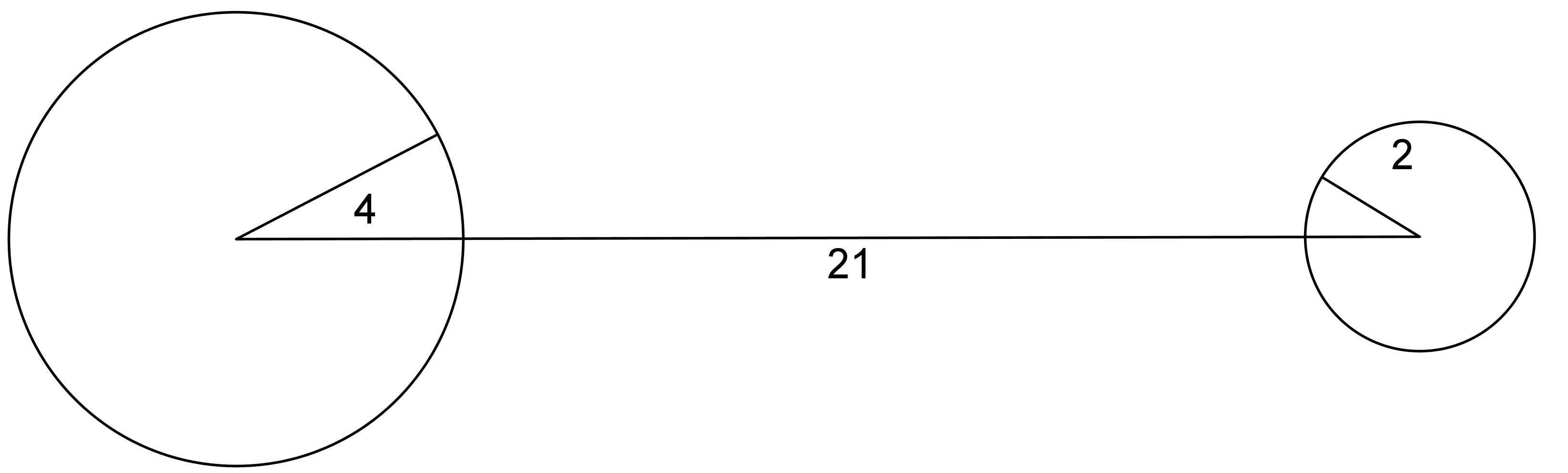
If we draw circles of radius 4 and 2 on the endpoints of the side of length 21 to represent positions for the shorter sides, we can see that there are no places for the short sides that would allow them to meet up and form a triangle.
In general, the longest side length must be less than the sum of the other two side lengths. If not, we can’t make a triangle!
If we can make a triangle with three given side lengths, it turns out that the measures of the corresponding angles will always be the same. For example, if two triangles have side lengths 3, 4, and 5, they will have the same corresponding angle measures.

 All of the possible positions of the endpoint of the moving side form a circle:
All of the possible positions of the endpoint of the moving side form a circle:

