Unit 6: Practice Problem Sets
Lesson 1
Problem 1 (from Unit 3, Lesson 7)
Lin and Tyler are drawing circles. Tyler's circle has twice the diameter of Lin’s circle. Tyler thinks that his circle will have twice the area of Lin’s circle as well. Do you agree with Tyler?
Problem 2 (from Unit 5, Lesson 15)
Jada and Priya are trying to solve the equation \frac23+x=4.
-
Jada says, “I think we should multiply each side by \frac32 because that is the reciprocal of \frac23.”
-
Priya says, “I think we should add \text-\frac23 to each side because that is the opposite of \frac23.”
-
Which person’s strategy should they use? Why?
-
Write an equation that can be solved using the other person’s strategy.
Problem 3 (from Unit 5, Lesson 13)
What are the missing operations?
- 48 ? (-8) = (-6)
- (-40) ? 8 =( -5)
- 12 ? (-2) = 14
- 18 ? (-12) = 6
- 18 ? (-20) = -2
- 22 ? (-0.5) = -11
Problem 4 (from Unit 5, Lesson 14)
In football, the team that has the ball has four chances to gain at least ten yards. If they don't gain at least ten yards, the other team gets the ball. Positive numbers represent a gain and negative numbers represent a loss. Select all of the sequences of four plays that result in the team getting to keep the ball.
- 8, -3, 4, 21
- 30, -7, -8, -12
- 2, 16, -5, -3
Problem 5
A sandwich store charges $20 to have 3 turkey subs delivered and $26 to have 4 delivered.
- Is the relationship between number of turkey subs delivered and amount charged proportional? Explain how you know.
- How much does the store charge for 1 additional turkey sub?
- Describe a rule for determining how much the store charges based on the number of turkey subs delivered.
Problem 6
Which question cannot be answered by the solution to the equation 3x=27?
- Elena read three times as many pages as Noah. She read 27 pages. How many pages did Noah read?
- Lin has 27 stickers. She gives 3 stickers to each of her friends. With how many friends did Lin share her stickers?
- Diego paid $27 to have 3 pizzas delivered and $35 to have 4 pizzas delivered. What is the price of one pizza?
- The coach splits a team of 27 students into 3 groups to practice skills. How many students are in each group?
Lesson 2
Problem 1 (from Unit 3, Lesson 1)
The table shows the number of apples and the total weight of the apples.
| number of apples | weight of apples (grams) | |
|---|---|---|
| row 1 | 2 | 511 |
| row 2 | 5 | 1200 |
| row 3 | 8 | 2016 |
Estimate the weight of 6 apples.
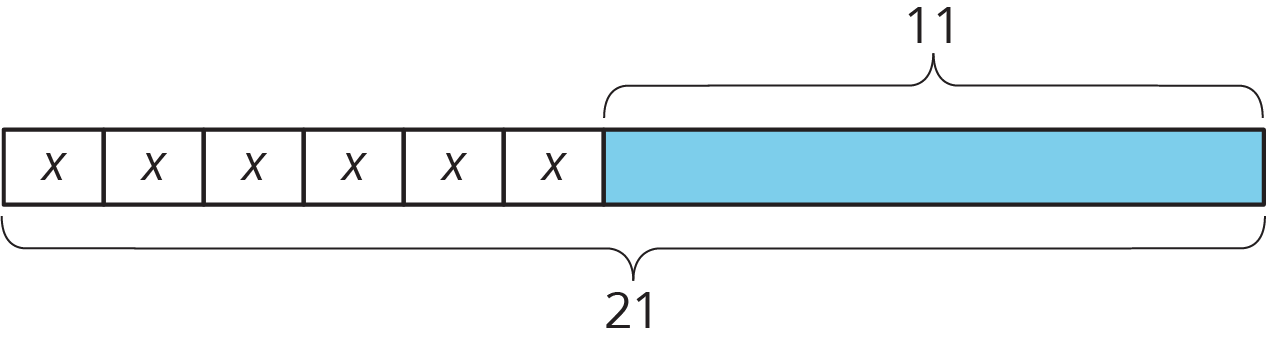
Problem 2
Select all stories that the tape diagram can represent.
- There are 87 children and 39 adults at a show. The seating in the theater is split into 4 equal sections.
- There are 87 first graders in after-care. After 39 students are picked up, the teacher put the remaining students into 4 groups for an activity.
- Lin buys a pack of 87 pencils. She gives 39 to her teacher and shared the remaining pencils between herself and 3 friends.
- Andre buys 4 packs of paper clips with 39 paper clips in each. Then he gives 87 paper clips to his teacher.
- Diego’s family spends $87 on 4 tickets to the fair and a $39 dinner.
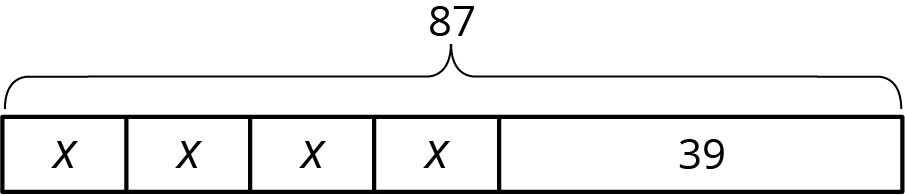
Problem 3
Andre wants to save $40 to buy a gift for his dad. Andre’s neighbor will pay him weekly to mow the lawn, but Andre always gives a $2 donation to the food bank in weeks when he earns money. Andre calculates that it will take him 5 weeks to earn the money for his dad’s gift. He draws a tape diagram to represent the situation.
- Explain how the parts of the tape diagram represent the story.
- How much does Andre’s neighbor pay him each week to mow the lawn?
Problem 4 (from Unit 5, Lesson 13)
Without evaluating each expression, determine which value is the greatest. Explain how you know.
- 7\frac56 - 9\frac34
- (\text-7\frac56) + (\text-9\frac34)
- (\text-7\frac56) \boldcdot 9\frac34
- (\text-7\frac56) \div (\text-9\frac34)
Problem 5 (from Unit 5, Lesson 15)
Solve each equation.
- (8.5) \boldcdot (\text-3) = a
- (\text-7) + b = (\text-11)
- c - (\text-3) = 15
- d \boldcdot (\text-4) = 32
Lesson 3
Problem 1 (from Unit 5, Lesson 15)
Solve each equation mentally.
- 2x = 10
- \text-3x = 21
- \frac13 x = 6
- \text-\frac12x = \text-7
Problem 2 (from Unit 5, Lesson 3)
Complete the magic squares so that the sum of each row, each column, and each diagonal in a grid are all equal.
Problem 3
Draw a tape diagram to match each equation.
-
5(x+1)=20
-
5x+1=20
Problem 4
Select all the equations that match the tape diagram.

- 35=8+x+x+x+x+x+x
- 35=8+6x
- 6+8x=35
- 6x+8=35
- 6x+8x=35x
- 35-8=6x
Problem 5 (from Unit 4, Lesson 2)
Each car is traveling at a constant speed. Find the number of miles each car travels in 1 hour at the given rate.
-
135 miles in 3 hours
-
22 miles in \frac12 hour
-
7.5 miles in \frac14 hour
-
\frac{100}{3} miles in \frac23 hour
-
97\frac12 miles in \frac32 hour
Lesson 4
Problem 1 (from Unit 3, Lesson 1)
Draw a square with side length 7 cm.
- Predict the perimeter and the length of the diagonal of the square.
- Measure the perimeter and the length of the diagonal of the square.
- Describe how close the predictions and measurements are.
Problem 2 (from Unit 5, Lesson 9)
Find the products.
- (100) \boldcdot (\text-0.09)
- (\text-7) \boldcdot (\text- 1.1)
- (\text-7.3) \boldcdot (5)
- (\text-0.2) \boldcdot (\text-0.3)
Problem 3
Here are three stories:
- A family buys 6 tickets to a show. They also pay a $3 parking fee. They spend $27 to see the show.
- Diego has 27 ounces of juice. He pours equal amounts for each of his 3 friends and has 6 ounces left for himself.
- Jada works for 6 hours preparing for the art fair. She spends 3 hours on a sculpture and then paints 27 picture frames.
Here are three equations:
- 3x+6=27
- 6x+3=27
- 27x+3=6
- Decide which equation represents each story. What does x represent in each equation?
- Find the solution to each equation. Explain or show your reasoning.
- What does each solution tell you about its situation?
Problem 4
Here is a diagram and its corresponding equation. Find the solution to the equation and explain your reasoning.
6x+11=21
Problem 5 (from Unit 5, Lesson 7)
- Plot these points on the coordinate plane:
A= (3, 2), B= (7.5, 2), C= (7.5, \text-2.5), D= (3, \text-2)

- What is the vertical difference between D and A?
- Write an expression that represents the vertical distance between B and C.
Lesson 5
Problem 1 (from Unit 4, Lesson 2)
Here are some prices customers paid for different items at a farmer’s market. Find the cost for 1 pound of each item.
- $5 for 4 pounds of apples
- $3.50 for \frac12 pound of cheese
- $8.25 for 1\frac12 pounds of coffee beans
- $6.75 for \frac34 pounds of fudge
- $5.50 for a 6\frac14 pound pumpkin
Problem 2 (from Unit 5, Lesson 9)
Find the products.
- \frac23 \boldcdot \left(\frac {\text{-}4}{5}\right)
- \left(\frac {\text{-}5}{7}\right) \boldcdot \left(\frac {\text7}{5}\right)
- \left(\frac {\text{-}2}{39}\right) \boldcdot 39
- \left(\frac {\text2}{5}\right) \boldcdot \left(\frac {\text{-}3}{4}\right)
Problem 3
Here are two stories:
- A family buys 6 tickets to a show. They also each spend $3 on a snack. They spend $24 on the show.
- Diego has 24 ounces of juice. He pours equal amounts for each of his 3 friends, and then adds 6 more ounces for each.
Here are two equations:
- 3(x+6)=24
- 6(x+3)=24
- Which equation represents which story?
- What does x represent in each equation?
- Find the solution to each equation. Explain or show your reasoning.
- What does each solution tell you about its situation?
Problem 4
Here is a diagram and its corresponding equation. Find the solution to the equation and explain your reasoning.
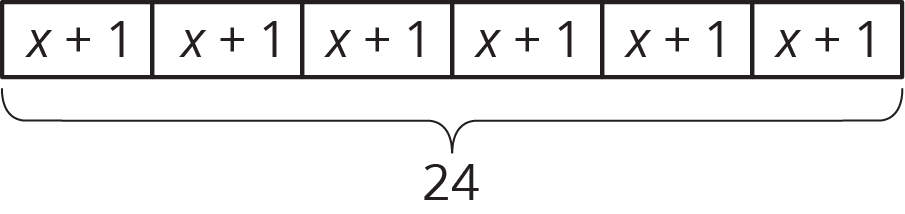
6(x+1)=24
Problem 5 (from Unit 5, Lesson 7)
Below is a set of data about temperatures. The range of a set of data is the distance between the lowest and highest value in the set. What is the range of these temperatures?
9^\circ \text{C}, \text-3^\circ \text{C}, 22^\circ \text{C}, \text-5^\circ \text{C}, 11^\circ \text{C}, 15^\circ \text{C}
Problem 6 (from Unit 4, Lesson 11)
A store is having a 25% off sale on all shirts. Show two different ways to calculate the sale price for a shirt that normally costs $24.
Lesson 6
Problem 1 (from Unit 6, Lesson 2)
A school ordered 3 large boxes of board markers. After giving 15 markers to each of 3 teachers, there were 90 markers left. The diagram represents the situation. How many markers were originally in each box?
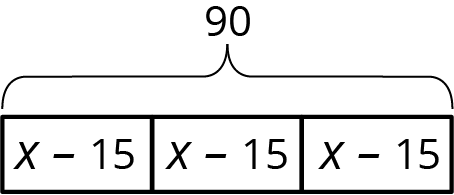
Problem 2 (from Unit 6, Lesson 3)
The diagram can be represented by the equation 25=2+6x. Explain where you can see the 6 in the diagram.

Problem 3
Elena walked 20 minutes more than Lin. Jada walked twice as long as Elena. Jada walked for 90 minutes. The equation 2(x+20)=90 describes this situation. Match each amount in the story with the expression that represents it.
- The number of minutes that Jada walked
- The number of minutes that Elena walked
- The number of minutes that Lin walked
- x
- x+20
- 2(x+20)
- 90
Problem 4
Match each equation to a story. (Two of the stories match the same equation.)
- 3(x+5)=17
- 3x+5=17
- 5(x+3)=17
- 5x+3=17
- Jada’s teacher fills a travel bag with 5 copies of a textbook. The weight of the bag and books is 17 pounds. The empty travel bag weighs 3 pounds. How much does each book weigh?
- A piece of scenery for the school play is in the shape of a 5-foot-long rectangle. The designer decides to increase the length. There will be 3 identical rectangles with a total length of 17 feet. By how much did the designer increase the length of each rectangle?
- Elena spends $17 and buys a $3 book and a bookmark for each of her 5 cousins. How much does each bookmark cost?
- Noah packs up bags at the food pantry to deliver to families. He packs 5 bags that weigh a total of 17 pounds. Each bag contains 3 pounds of groceries and a packet of papers with health-related information. How much does each packet of papers weigh?
- Andre has 3 times as many pencils as Noah and 5 pens. He has 17 pens and pencils all together. How many pencils does Noah have?
Lesson 7
Problem 1 (from Unit 2, Lesson 11)
There is a proportional relationship between the volume of a sample of helium in liters and the mass of that sample in grams. If the mass of a sample is 5 grams, its volume is 28 liters. (5, 28) is shown on the graph below.
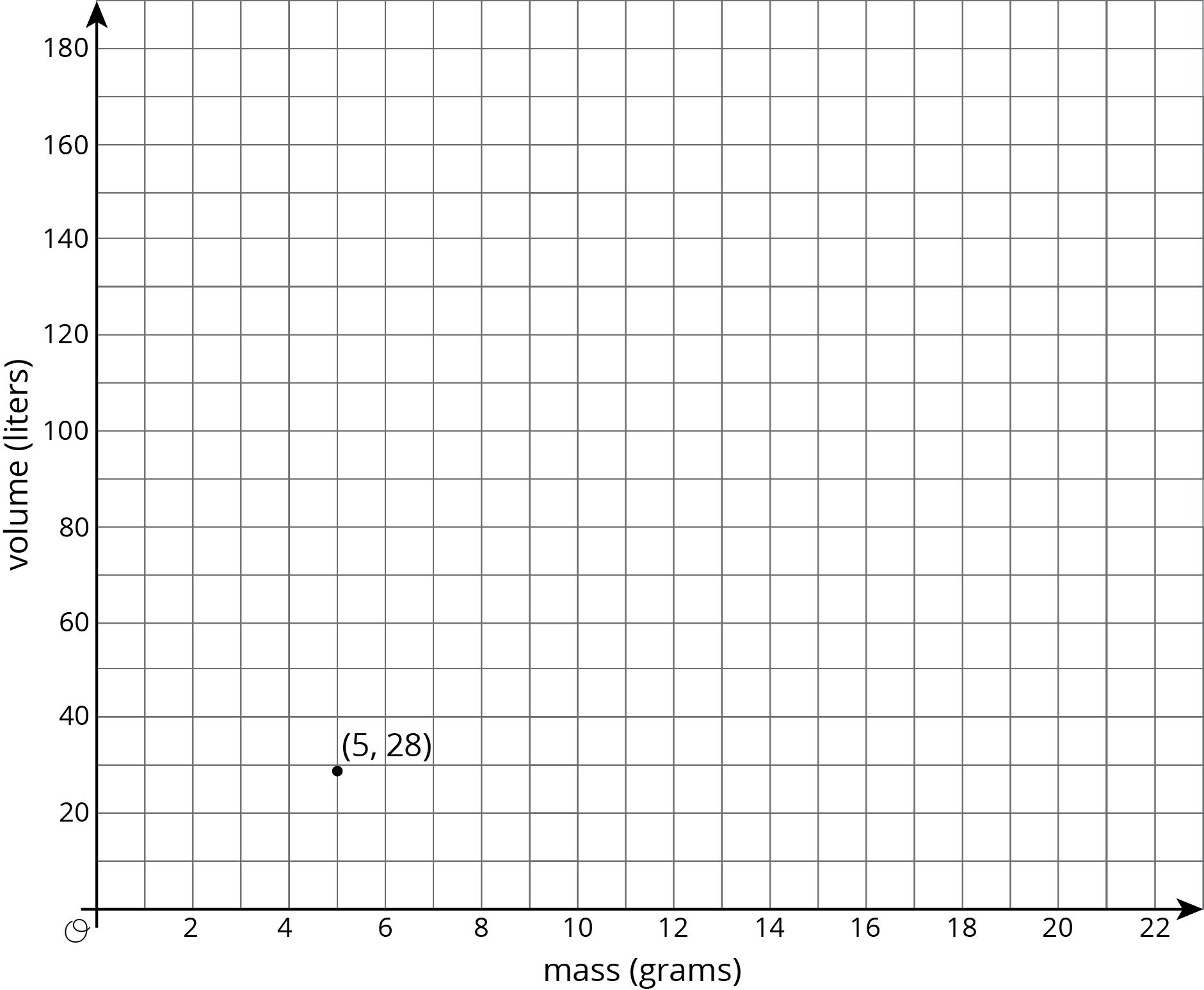
- What is the constant of proportionality in this relationship?
- In this situation, what is the meaning of the number you found in part a?
- Add at least three more points to the graph above, and label with their coordinates.
- Write an equation that shows the relationship between the mass of a sample of helium and its volume. Use m for mass and v for volume.
Problem 2
Explain how the parts of the balanced hanger compare to the parts of the equation.
7=2x+3
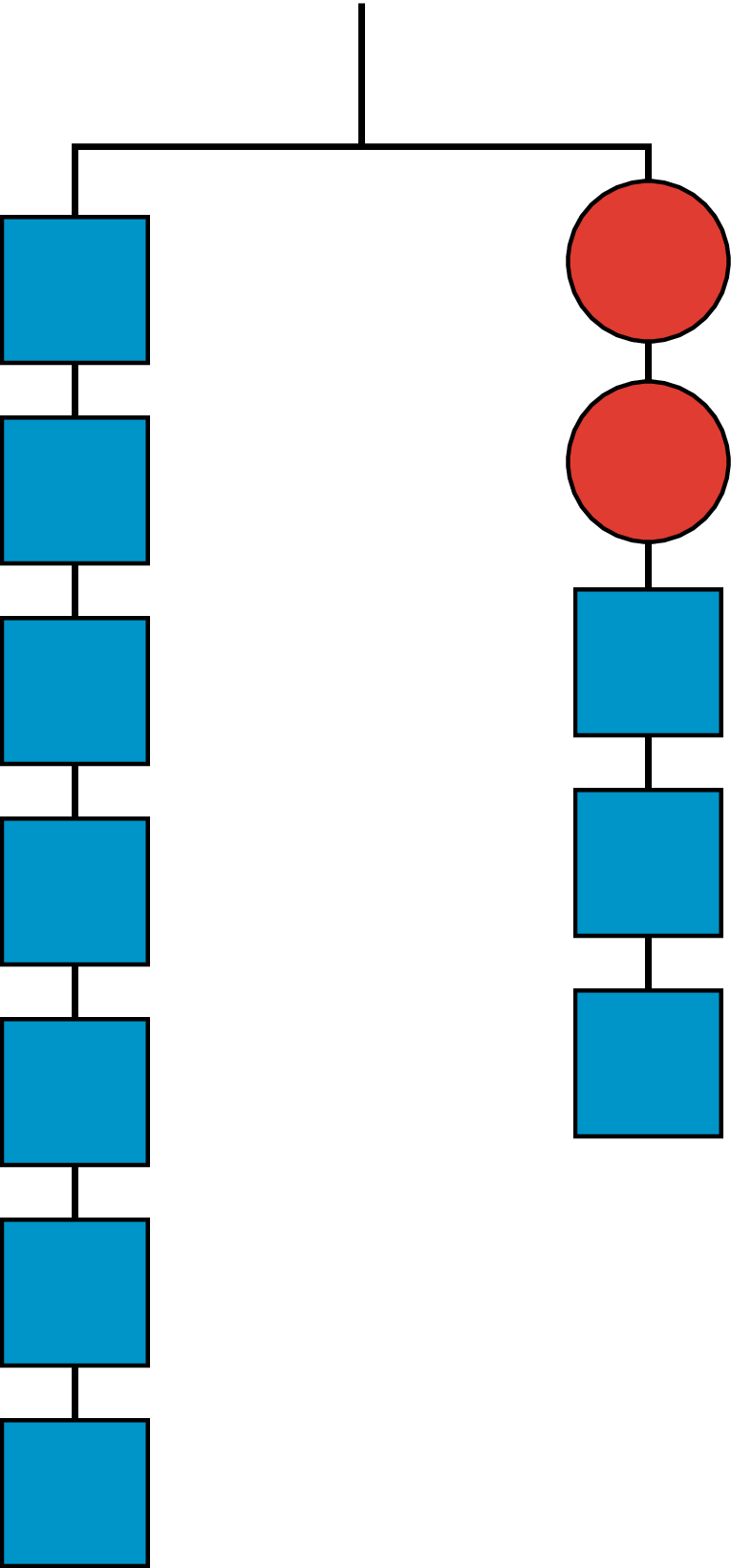
Problem 3
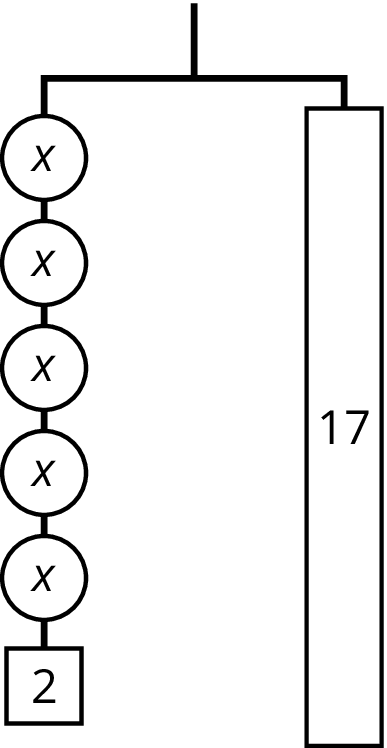
- Write an equation to represent the hanger.
- Draw more hangers to show each step you would take to find x. Explain your reasoning.
- Write an equation to describe each hanger you drew. Describe how each equation matches its hanger.
Lesson 8
Problem 1
Here is a hanger:
- Write an equation to represent the hanger.
- Solve the equation by reasoning about the equation or the hanger. Explain your reasoning.
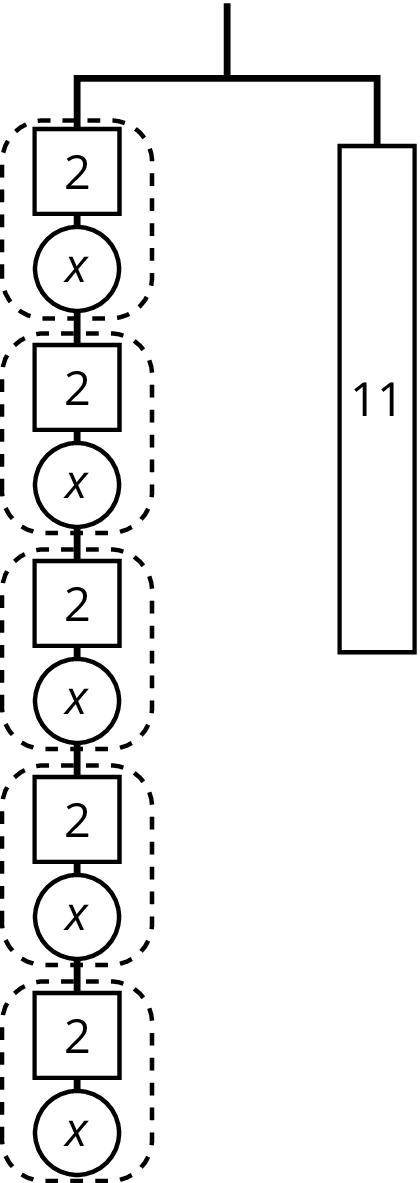
Problem 2
Explain how each part of the equation 9=3(x+2) is represented in the hanger.
- x
- 9
- 3
- x+2
- 3(x+2)
- the equal sign

Problem 3 (from Unit 4, Lesson 11)
Select the word from the following list that best describes each situation.
- Tax
- Commission
- Discount
- Markup
- Tip or gratuity
- Interest
- You deposit money in a savings account, and every year the amount of money in the account increases by 2.5%.
- For every car sold, a car salesman is paid 6% of the car’s price.
- Someone who eats at a restaurant pays an extra 20% of the food price. This extra money is kept by the person who served the food.
- An antique furniture store pays $200 for a chair, adds 50% of that amount, and sells the chair for $300.
- The normal price of a mattress is $600, but it is on sale for 10% off.
- For any item you purchase in Texas, you pay an additional 6.25% of the item's price to the state government.
Problem 4 (from Unit 6, Lesson 3)
Clare drew this diagram to match the equation 2x+16=50, but she got the wrong solution as a result of using this diagram.
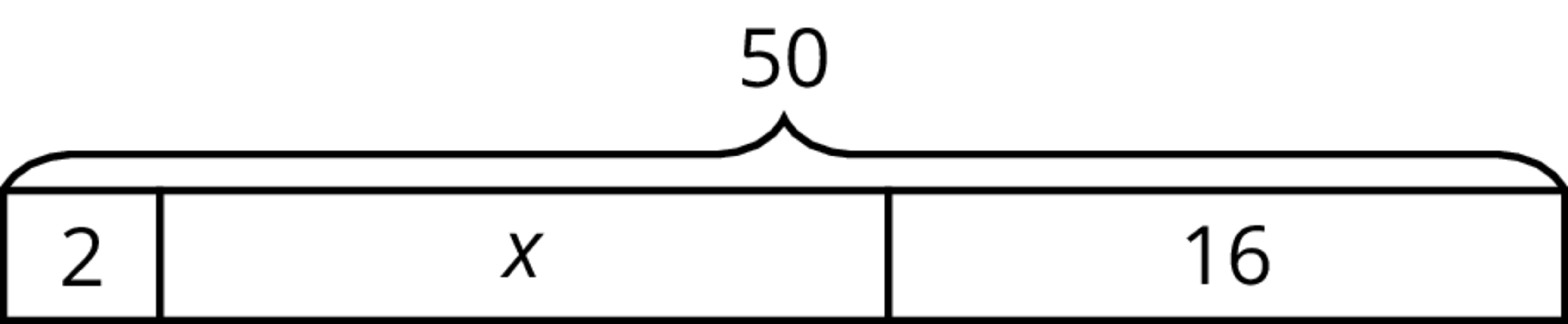
- What value for x can be found using the diagram?
- Show how to fix Clare’s diagram to correctly match the equation.
- Use the new diagram to find a correct value for x.
- Explain the mistake Clare made when she drew her diagram.
Lesson 9
Problem 1
Solve each equation.
- 4x=\text-28
- x-\text-6=\text-2
- \text-x+4=\text-9
- \text-3x+7=1
- 25x+\text-11=\text-86
Problem 2
Here is an equation 2x+9=\text-15. Write three different equations that have the same solution as 2x+9=\text-15. Show or explain how you found them.
Problem 3 (from Unit 6, Lesson 3)
Select all the equations that match the diagram.
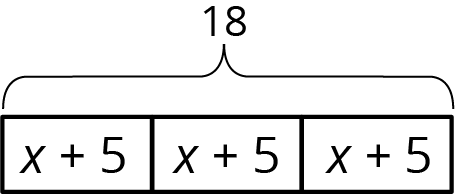
- x+5=18
- 18\div3=x+5
- 3(x+5)=18
- x+5 = \frac13\boldcdot 18
- 3x+5=18
Problem 4 (from Unit 6, Lesson 4)
Match each story to an equation.
- A stack of nested paper cups is 8 inches tall. The first cup is 4 inches tall and each of the rest of the cups in the stack adds \frac14 inch to the height of the stack.
- A baker uses 4 cups of flour. She uses \frac14 cup to flour the counters and the rest to make 8 identical muffins.
- Elena has an 8-foot piece of ribbon. She cuts off a piece that is \frac14 of a foot long and cuts the remainder into four pieces of equal length.
- \frac14 + 4x=8
- 4+\frac14x=8
- 8x +\frac14=4
Problem 5 (from Unit 6, Lesson 2)
There are 88 seats in a theater. The seating in the theater is split into 4 identical sections. Each section has 14 red seats and some blue seats.
- Draw a tape diagram to represent the situation.
- What unknown amounts can be found by by using the diagram or reasoning about the situation?
Lesson 10
Problem 1 (from Unit 4, Lesson 11)
Andre wants to buy a backpack. The normal price of the backpack is $40. He notices that a store that sells the backpack is having a 30% off sale. What is the sale price of the backpack?
Problem 2 (from Unit 4, Lesson 12)
On the first math exam, 16 students received an A grade. On the second math exam, 12 students received an A grade. What percentage decrease is that?
Problem 3
Solve each equation.
- 2(x-3) = 14
- \text-5(x-1) = 40
- 12(x+10)=24
- \frac16(x+6)=11
- \frac57(x-9)=25
Problem 4
Select all expressions that represent a correct solution to the equation 6(x+4)=20.
- (20-4)\div 6
- \frac16(20-4)
- 20-6-4
- 20\div6-4
- \frac16(20-24)
- (20-24)\div 6
Problem 5
Lin and Noah are solving the equation 7(x+2)=91.
Lin starts by using the distributive property. Noah starts by dividing each side by 7.
- Show what Lin's and Noah's full solution methods might look like.
- What is the same and what is different about their methods?
Lesson 11
Problem 1 (from Unit 5, Lesson 9)
Find the value of each variable.
- a \boldcdot 3 = \text-30
- \text-9\boldcdot b = 45
- \text-89 \boldcdot 12 =c
- d \boldcdot 88 = \text-88,\!000
Problem 2
Match each equation to its solution and to the story it describes.
Equations:
- 5x-7=3
- 7=3(5+x)
- 3x+5=\text-7
- \frac13(x+7)=5
Solutions:
- -4
- \frac {\text{-}8}{3}
- 2
- 8
Stories:
- The temperature is \text-7. Since midnight the temperature tripled and then rose 5 degrees. What was temperature at midnight?
- Jada has 7 pink roses and some white roses. She gives all of them away: 5 roses to each of her 3 favorite teachers. How many white roses did she give away?
- A musical instrument company reduced the time it takes for a worker to build a guitar. Before the reduction it took 5 hours. Now in 7 hours they can build 3 guitars. By how much did they reduce the time it takes to build each guitar?
- A club puts its members into 5 groups for an activity. After 7 students have to leave early, there are only 3 students left to finish the activity. How many students were in each group?
Problem 3
The baby giraffe weighed 132 pounds at birth. He gained weight at a steady rate for the first 7 months until his weight reached 538 pounds. How much did he gain each month?
Problem 4
Six teams are out on the field playing soccer. The teams all have the same number of players. The head coach asks for 2 players from each team to come help him move some equipment. Now there are 78 players on the field. Write and solve an equation whose solution is the number of players on each team.
Problem 5 (from Unit 4, Lesson 7)
A small town had a population of 960 people last year. The population grew to 1200 people this year. By what percentage did the population grow?

Problem 6 (from Unit 4, Lesson 7)
The gas tank of a truck holds 30 gallons. The gas tank of a passenger car holds 50% less. How many gallons does it hold?

Lesson 12
Problem 1 (from Unit 4, Lesson 12)
A backpack normally costs $25 but it is on sale for $21. What percentage is the discount?
Problem 2 (from Unit 5, Lesson 9)
Find each product.
- \frac25 \boldcdot (\text-10)
- \text-8 \boldcdot \left(\frac {\text{-}3}{2}\right)
- \frac{10}{6} \boldcdot 0.6
- \left(\frac {\text{-}100}{37}\right) \boldcdot (\text-0.37)
Problem 3
Select all expressions that show x increased by 35%.
- 1.35x
- \frac{35}{100}x
- x + \frac{35}{100}x
- ( 1+0.35)x
- \frac{100+35}{100}x
- (100 + 35)x
Problem 4 (from Unit 4, Lesson 11)
Complete each sentence with the word discount, deposit, or withdrawal.
- Clare took $20 out of her bank account. She made a _____.
- Kiran used a coupon when he bought a pair of shoes. He got a _____.
- Priya put $20 into her bank account. She made a _____.
- Lin paid less than usual for a pack of gum because it was on sale. She got a _____.
Problem 5
Here are two stories:
- The initial freshman class at a college is 10% smaller than last year’s class. But then during the first week of classes, 20 more students enroll. There are then 830 students in the freshman class.
- A store reduces the price of a computer by $20. Then during a 10% off sale, a customer pays $830.
Here are two equations:
- 0.9x+20=830
- 0.9(x-20)=830
- Decide which equation represents each story.
- Explain why one equation has parentheses and the other doesn’t.
- Solve each equation, and explain what the solution means in the situation.
Lesson 13
Problem 1
For each inequality, find two values for x that make the inequality true and two values that make it false.
- x+3>70
- x+3<70
- \text-5x<2
- 5x<2
Problem 2
Here is an inequality: \text-3x > 18.
- List some values for x that would make this inequality true.
- How are the solutions to the inequality \text-3x \geq 18 different from the solutions to \text-3x > 18? Explain your reasoning.
Problem 3
Match each sentence with the inequality that could represent the situation.
- Han got $2 from Clare, but still has less than $20.
- Mai spent $2 and has less than $20.
- If Tyler had twice the amount of money he has, he would have less than $20.
- If Priya had half the money she has, she would have less than $20.
- x-2<20
- 2x<20
- x+2<20
- \frac12x<20
Problem 4 (from Unit 4, Lesson 12)
Here are the prices for cheese pizza at a certain pizzeria:
| pizza size | price in dollars | |
|---|---|---|
| row 1 | small | 11.60 |
| row 2 | medium | |
| row 3 | large | 16.25 |
-
You had a coupon that made the price of a large pizza $13.00. For what percent off was the coupon?
-
Your friend purchased a medium pizza for $10.31 with a 30% off coupon. What is the price of a medium pizza without a coupon?
-
Your friend has a 15% off coupon and $10. What is the largest pizza that your friend can afford, and how much money will be left over after the purchase?
Problem 5 (from Unit 6, Lesson 4)
Select all the stories that can be represented by the diagram.
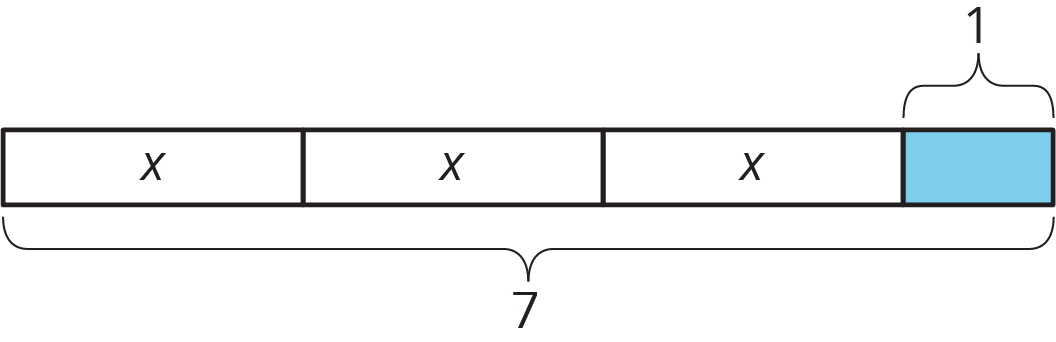
- Andre studies 7 hours this week for end-of-year exams. He spends 1 hour on English and an equal number of hours each on math, science, and history.
- Lin spends $3 on 7 markers and a $1 pen.
- Diego spends $1 on 7 stickers and 3 marbles.
- Noah shares 7 grapes with 3 friends. He eats 1 and gives each friend the same number of grapes.
- Elena spends $7 on 3 notebooks and a $1 pen.
Lesson 14
Problem 1
The solution to 5-3x > 35 is either x>\text-10 or \text-10>x. Which solution is correct? Explain how you know.
Problem 2
The school band director determined from past experience that if they charge t dollars for a ticket to the concert, they can expect attendance of 1000-50t. The director used this model to figure out that the ticket price needs to be $8 or greater in order for at least 600 to attend. Do you agree with this claim? Why or why not?
Problem 3 (from Unit 6, Lesson 13)
Which inequality is true when the value of x is -3?
- \text-x -6 < \text-3.5
- \text-x- 6 >3.5
- \text-x -6 > \text-3.5
- x -6 > \text-3.5
Problem 4 (from Unit 6, Lesson 13)
Draw the solution set for each of the following inequalities.
-
x\leq5
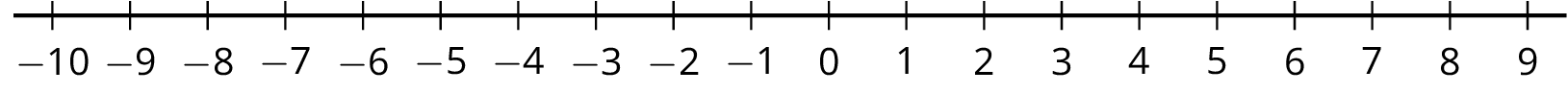
-
x<\frac52
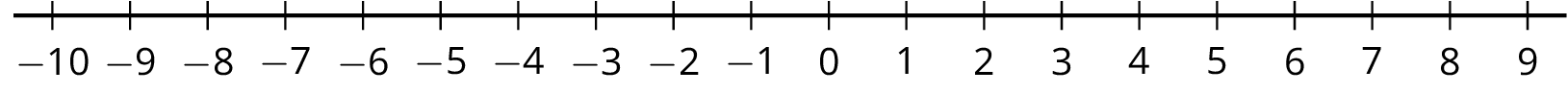
Problem 5 (from Unit 6, Lesson 3)
Write three different equations that match the tape diagram.

Problem 6 (from Unit 6, Lesson 2)
A baker wants to reduce the amount of sugar in his cake recipes. He decides to reduce the amount used in 1 cake by \frac12 cup. He then uses 4\frac12 cups of sugar to bake 6 cakes.
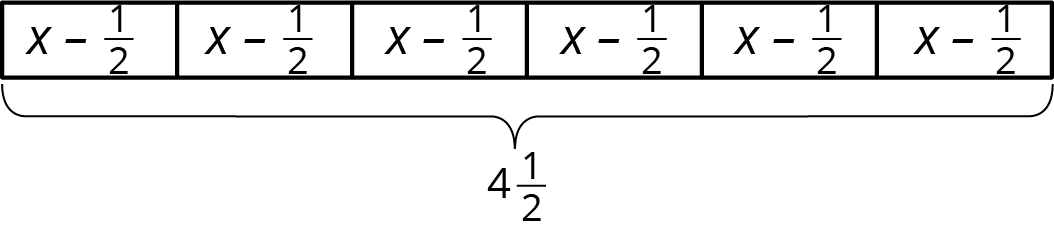
- Describe how the tape diagram represents the story.
- How much sugar was originally in each cake recipe?
Problem 7 (from Unit 4, Lesson 12)
One year ago, Clare was 4 feet 6 inches tall. Now Clare is 4 feet 10 inches tall. By what percentage did Clare’s height increase in the last year?
Lesson 15
Problem 1
- Consider the inequality \text-1 \leq \frac{x}{2}.
- Predict which values of x will make the inequality true.
- Complete the table to check your prediction.
x -4 -3 -2 -1 0 1 2 3 4 \frac{x}{2}
- Consider the inequality 1 \leq \frac {\text{-}x}{2}.
- Predict which values of x will make it true.
- Complete the table to check your prediction.
x -4 -3 -2 -1 0 1 2 3 4 \text-\frac{x}{2}
Problem 2
Diego is solving the inequality 100-3x \ge \text-50. He solves the equation 100-3x = \text-50 and gets x=50. What is the solution to the inequality?
- x < 50
- x \le 50
- x > 50
- x \ge 50
Problem 3
Problem 4 (from Unit 6, Lesson 13)
Select all values of x that make the inequality \text-x+6\ge10 true.
- -3.9
- 4
- -4.01
- -4
- 4.01
- 3.9
- 0
- -7
Problem 5 (from Unit 6, Lesson 13)
Draw the solution set for each of the following inequalities.
-
x>7
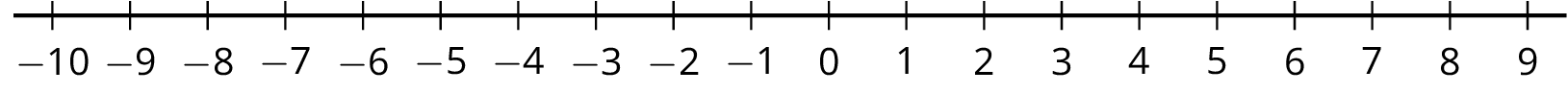
-
x\geq\text-4.2
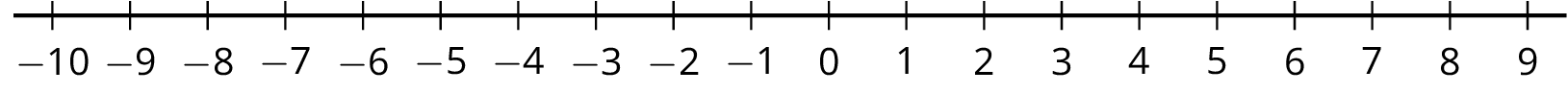
Problem 6 (from Unit 4, Lesson 12)
The price of a pair of earrings is $22 but Priya buys them on sale for $13.20.
- By how much was the price discounted?
- What was the percentage of the discount?
Lesson 16
Problem 1
Priya looks at the inequality 12-x>5 and says “I subtract a number from 12 and want a result that is bigger than 5. That means that the solutions should be values of x that are smaller than something.”
Do you agree with Priya? Explain your reasoning and include solutions to the inequality in your explanation.
Problem 2
When a store had sold \frac25 of the shirts that were on display, they brought out another 30 from the stockroom. The store likes to keep at least 150 shirts on display. The manager wrote the inequality \frac35x+30 \geq 150 to describe the situation.
- Explain what \frac35 means in the inequality.
- Solve the inequality.
- Explain what the solution means in the situation.
Problem 3 (from Unit 6, Lesson 13)
You know x is a number less than 4. Select all the inequalities that must be true.
- x<2
- x+6<10
- 5x<20
- x-2>2
- x<8
Problem 4 (from Unit 6, Lesson 13)
Here is an unbalanced hanger.
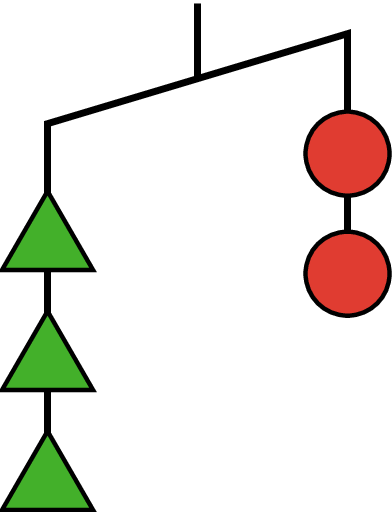
- If you knew each circle weighed 6 grams, what would that tell you about the weight of each triangle? Explain your reasoning.
- If you knew each triangle weighed 3 grams, what would that tell you about the weight of each circle? Explain your reasoning.
Problem 5 (from Unit 4, Lesson 12)
At a skateboard shop:
- The price tag on a shirt says $12.58. Sales tax is 7.5% of the price. How much will you pay for the shirt?
- The store buys a helmet for $19.00 and sells it for $31.50. What percentage was the markup?
- The shop pays workers $14.25 per hour plus 5.5% commission. If someone works 18 hours and sells $250 worth of merchandise, what is the total amount of their paycheck for this pay period? Explain or show your reasoning.
Lesson 17
Problem 1
28 students travel on a field trip. They bring a van that can seat 12 students. Elena and Kiran’s teacher asks parents to drive cars that seat 3 children each to transport the rest of the students.
Elena wonders if she should use the inequality 12+3n>28 or 12+3n\geq28 to figure out how many cars are needed. Kiran doesn’t think it matters in this case. Do you agree with Kiran? Explain your reasoning.
Problem 2
- In the cafeteria, there is one large 10-seat table and many smaller 4-seat tables. There are enough tables to fit 200 students. Write an inequality whose solution is the possible number of 4-seat tables in the cafeteria.
- 5 barrels catch rainwater in the schoolyard. Four barrels are the same size, and the fifth barrel holds 10 liters of water. Combined, the 5 barrels can hold at least 200 liters of water. Write an inequality whose solution is the possible size of each of the 4 barrels.
- How are these two problems similar? How are they different?
Problem 3 (from Unit 6, Lesson 9)
Solve each equation.
- 5(n-4)=\text-60
- \text-3t+ \text-8=25
- 7p-8=\text-22
- \frac25(j+40)=\text-4
- 4(w+1)=\text-6
Problem 4 (from Unit 6, Lesson 13)
Select all the inequalities that have the same graph as x<4.
- x<2
- x+6<10
- 5x<20
- x-2>2
- x<8
Problem 5 (from Unit 4, Lesson 12)
A 200 pound person weighs 33 pounds on the moon.
-
How much did the person’s weight decrease?
-
By what percentage did the person’s weight decrease?
Lesson 18
Problem 1
For each expression, write an equivalent expression that uses only addition.
- 20-9+8-7
- 4x-7y-5z+6
- \text-3x-8y-4-\frac87z
Problem 2
Use the distributive property to write an expression that is equivalent to each expression. If you get stuck, consider drawing boxes to help organize your work.
- 9(4x-3y-\frac23)
- \text-2(\text-6x+3y-1)
- \frac15(20y-4x-13)
- 8(\text-x-\frac12)
- \text-8(\text-x-\frac34y+\frac72)
Problem 3
Kiran wrote the expression x-10 for this number puzzle: “Pick a number, add -2, and multiply by 5.”
Lin thinks Kiran made a mistake.
- How can she convince Kiran he made a mistake?
- What would be a correct expression for this number puzzle?
Problem 4 (from Unit 2, Lesson 7)
The output from a coal power plant is shown in the table:
| energy in megawatts | number of days | |
|---|---|---|
| row 1 | 1,200 | 2.4 |
| row 2 | 1,800 | 3.6 |
| row 3 | 4,000 | 8 |
| row 4 | 10,000 | 20 |
Similarly, the output from a solar power plant is shown in the table:
| energy in megawatts | number of days | |
|---|---|---|
| row 1 | 100 | 1 |
| row 2 | 650 | 4 |
| row 3 | 1,200 | 7 |
| row 4 | 1,750 | 10 |
Based on the tables, is the energy output in proportion to the number of days for either plant? If so, write an equation showing the relationship. If not, explain your reasoning.
Lesson 19
Problem 1
- Expand to write an equivalent expression: \frac {\text{-}1}{4}(\text-8x+12y)
- Factor to write an equivalent expression: 36a-16
Problem 2
Lin missed math class on the day they worked on expanding and factoring. Kiran is helping Lin catch up.
- Lin understands that expanding is using the distributive property, but she doesn’t understand what factoring is or why it works. How can Kiran explain factoring to Lin?
- Lin asks Kiran how the diagrams with boxes help with factoring. What should Kiran tell Lin about the boxes?
- Lin asks Kiran to help her factor the expression \text-4xy-12xz+20xw. How can Kiran use this example to Lin understand factoring?
Problem 3
Complete the equation with numbers that makes the expression on the right side of the equal sign equivalent to the expression on the left side.
Problem 4 (from Unit 4, Lesson 3)
Elena makes her favorite shade of purple paint by mixing 3 cups of blue paint, 1\frac12 cups of red paint, and \frac{1}{2} of a cup of white paint. Elena has \frac{2}{3} of a cup of white paint.
- Assuming she has enough red paint and blue paint, how much purple paint can Elena make?
- How much blue paint and red paint will Elena need to use with the \frac{2}{3} of a cup of white paint?
Problem 5 (from Unit 6, Lesson 9)
Solve each equation.
- \frac {\text{-}1}{8}d-4=\frac {\text{-}3}{8}
- \frac {\text{-}1}{4}m+5=16
- 10b+\text-45=\text-43
- \text-8(y-1.25)=4
- 3.2(s+10)=32
Problem 6 (from Unit 6, Lesson 13)
Select all the inequalities that have the same solutions as \text-4x<20.
- \text-x<5
- 4x>\text-20
- 4x<\text-20
- x<\text-5
- x>5
- x>\text-5
Lesson 20
Problem 1
Andre says that 10x+6 and 5x+11 are equivalent because they both equal 16 when x is 1. Do you agree with Andre? Explain your reasoning.
Problem 2
Select all expressions that can be subtracted from 9x to result in the expression 3x+5.
- \text-5+6x
- 5-6x
- 6x+5
- 6x-5
- \text-6x+5
Problem 3
Select all the statements that are true for any value of x.
- 7x + (2x+7) = 9x+7
- 7x+(2x-1)=9x+1
- 3x + (10 - 3x)=10
- 5x - (8 - 6x) =\text-x-8
- 4x - (2x+8) =2x-8
- 6x - (2x -4)=4x+4
Problem 4 (from Unit 6, Lesson 13)
For each situation, would you describe it with x< 25, x > 25, x \leq 25, or x \geq 25?
- The library is having a party for any student who read at least 25 books over the summer. Priya read x books and was invited to the party.
- Kiran read x books over the summer but was not invited to the party.
-

-

Problem 5 (from Unit 2, Lesson 9)
Consider the problem: A water bucket is being filled with water from a water faucet at a constant rate. When will the bucket be full? What information would you need to be able to solve the problem?
Lesson 21
Problem 1
- Noah says that 9x - 2x + 4x is equivalent to 3x, because the subtraction sign tells us to subtract everything that comes after 9x.
- Elena says that 9x - 2x + 4x is equivalent to 11x, because the subtraction only applies to 2x.
Do you agree with either of them? Explain your reasoning.
Problem 2
Identify the error in generating an expression equivalent to 4+2x-\frac12(10-4x). Then correct the error.
4+2x + \frac {\text{-}1}{2}(10 + \text-4x) \\ 4+2x +\text-5 +2x \\ 4+2x-5+2x \\ \text-1
Problem 3
Select all expressions that are equivalent to 5x -15 - 20x+10.
- 5x - (15+20x) + 10
- 5x+\text-15+\text-20x+10
- 5(x-3-4x+2)
- \text-5(\text-x +3+4x+\text-2)
- \text-15x-5
- \text-5(3x+1)
Problem 4 (from Unit 6, Lesson 14)
The school marching band has a budget of up to $750 to cover 15 new uniforms and competition fees that total $300. How much can they spend for one uniform?
- Write an inequality to represent this situation.
- Solve the inequality and describe what it means in the situation.
Problem 5 (from Unit 6, Lesson 16)
Solve the inequality that represents each story. Then interpret what the solution means in the story.
- For every $9 that Elena earns, she gives x dollars to charity. This happens 7 times this month. Elena wants to be sure she keeps at least $42 from this month’s earnings. 7(9-x) \geq 42
- Lin buys a candle that is 9 inches tall and burns down x inches per minute. She wants to let the candle burn for 7 minutes until it is less than 6 inches tall. 9 - 7x < 6
Problem 6 (from Unit 4, Lesson 3)
A certain shade of blue paint is made by mixing 1\frac12 quarts of blue paint with 5 quarts of white paint. If you need a total of 16.25 gallons of this shade of blue paint, how much of each color should you mix?
Lesson 22
Problem 1
Jada says, “I can tell that \frac {\text{-}2}{3}(x+5)+4(x+5)-\frac{10}{3}(x+5) equals 0 just by looking at it.” Is Jada correct? Explain how you know.
Problem 2
In each row, decide whether the expression in column A is equivalent to the expression in column B. If they are not equivalent, show how to change one expression to make them equivalent.
A
- 3x-2x+0.5x
- 3(x+4) - 2(x+4)
- 6(x+4)-2(x+5)
- 3(x+4) - 2(x+4) +0.5(x+4)
B
- 1.5x
- x+3
- 2(2x+7)
- 1.5
Problem 3 (from Unit 6, Lesson 20)
For each situation, write an expression for the new balance using as few terms as possible.
- A checking account has a balance of -$126.89. A customer makes two deposits, one 3\frac12 times the other, and then withdraws $25.
- A checking account has a balance of $350. A customer makes two withdrawals, one $50 more than the other. Then he makes a deposit of $75.
Problem 4 (from Unit 6, Lesson 21)
Tyler is using the distributive property on the expression 9-4(5x-6). Here is his work:
9-4(5x-6) \\ 9+(\text-4)(5x+\text-6) \\ 9+\text-20x + \text-6 \\ 3-20x
Mai thinks Tyler’s answer is incorrect. She says, “If expressions are equivalent then they are equal for any value of the variable. Why don’t you try to substitute the same value for x in all the equations and see where they are not equal?”
- Find the step where Tyler made an error.
- Explain what he did wrong.
- Correct Tyler’s work.
Problem 5 (from Unit 6, Lesson 13)
- If (11 + x) is positive, but (4 + x) is negative, what is one number that x could be?
- If (\text- 3 + y) is positive, but (\text- 9 + y) is negative, what is one number that y could be?
- If (\text- 5 + z) is positive, but (\text- 6 + z) is negative, what is one number that z could be?