- 3 _____ -3
- 12 _____ 24
- -12 _____ -24
- 5 _____ -(-5)
- 7.2 _____ 7
Unit 5: Practice Problem Sets
Lesson 1
Problem 1
It was \text- 5 ^\circ \text{C} in Copenhagen and \text- 12 ^\circ \text{C} in Oslo. Which city was colder?
Problem 2
- A fish is 12 meters below the surface of the ocean. What is its elevation?
- A sea bird is 28 meters above the surface of the ocean. What is its elevation?
- If the bird is directly above the fish, how far apart are they?
Problem 3
Compare using >, =, or <.
- -7.2 _____ -7
- -1.5 _____ \frac {\text{-}3}{2}
- \frac {\text{-}4}{5} _____ \frac {\text{-}5}{4}
- \frac {\text{-}3}{5} _____ \frac {\text{-}6}{10}
- \frac {\text{-}2}{3} _____ \frac13
Problem 4 (from Unit 4, Lesson 7)
Problem 5 (from Unit 2, Lesson 1)
A type of green paint is made by mixing 2 cups of yellow with 3.5 cups of blue.
-
Find a mixture that will make the same shade of green but a smaller amount.
-
Find a mixture that will make the same shade of green but a larger amount.
-
Find a mixture that will make the different shade of green that is bluer.
-
Find a mixture that will make the different shade of green that is more yellow.
Lesson 2
Problem 1
- The temperature is -2^\circ \text{C}. If the temperature rises by 15^\circ \text{C}, what is the new temperature?
- At midnight the temperature is -6^\circ \text{C}. At midday the temperature is 9^\circ \text{C}. By how much did the temperature rise?
Problem 2 (from Unit 5, Lesson 1)
Complete each statement with a number that makes the statement true.
- _____ < 7^\circ \text{C}
- _____ < \text- 3^\circ \text{C}
- \text- 0.8^\circ \text{C} < _____ < \text- 0.1^\circ \text{C}
- _____ > \text- 2^\circ \text{C}
Problem 3
Draw a diagram to represent each of these situations. Then write an addition expression that represents the final temperature.
- The temperature was 80 ^\circ \text{F} and then fell 20 ^\circ \text{F}.
- The temperature was \text-13 ^\circ \text{F} and then rose 9 ^\circ \text{F}.
- The temperature was \text-5 ^\circ \text{F} and then fell 8 ^\circ \text{F}.
Problem 4 (from Unit 2, Lesson 7)
Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?
-
The number of wheels on a group of buses.
row 1 number of buses number of wheels wheels per bus row 2 5 30 row 3 8 48 row 4 10 60 row 5 15 90 -
The number of wheels on a train.
row 1 number of train cars number of wheels wheels per train car row 2 20 184 row 3 30 264 row 4 40 344 row 5 50 424
Problem 5 (from Unit 4, Lesson 7)
Noah was assigned to make 64 cookies for the bake sale. He made 125% of that number. 90% of the cookies he made were sold. How many of Noah's cookies were left after the bake sale?
Lesson 3
Problem 1 (from Unit 2, Lesson 7)
Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?
-
Annie’s Attic is giving away $5 off coupons.
original price sale price row 1 $15 $10 row 2 $25 $20 row 3 $35 $30 -
Bettie's Boutique is having a 20% off sale.
original price sale price row 1 $15 $12 row 2 $25 $20 row 3 $35 $28
Problem 2
What is the final elevation if
- A bird starts at 20 m and changes 16 m?
- A butterfly starts at 20 m and changes -16 m?
- A diver starts at 5 m and changes -16 m?
- A whale starts at -9 m and changes 11 m?
- A fish starts at -9 meters and changes -11 meters?
Problem 3
One of the particles in an atom is called an electron. It has a charge of -1. Another particle in an atom is a proton. It has charge of +1. The charge of an atom is the sum of the charges of the electrons and the protons. A carbon atom has an overall charge of 0, because it has 6 electrons and 6 protons and \text- 6 + 6 = 0. Find the overall charge for the rest of the elements on the list.
| charge from electrons |
charge from protons |
overall charge |
|
|---|---|---|---|
| carbon | -6 | +6 | 0 |
| neon | -10 | +10 | |
| oxide | -10 | +8 | |
| copper | -27 | +29 | |
| tin | -50 | +50 |
Problem 4 (from Unit 4, Lesson 8)
Last week, the price, in dollars, of a gallon of gasoline was g. This week, the price of gasoline per gallon increased by 5%. Which expressions represent this week's price, in dollars, of a gallon of gasoline? Select all that apply.
- g + 0.05
- g + 0.05g
- 1.05g
- 0.05g
- (1+0.05)g
Problem 5
Add.
- 14.7 +28.9
- \text-9.2 + 4.4
- \text-81.4 + (\text-12)
- 51.8 + (\text-0.8)
Lesson 4
Problem 1 (from Unit 2, Lesson 8)
Decide whether or not each equation represents a proportional relationship.
- Volume measured in cups (c) vs. the same volume measured in ounces (z): c = \frac18 z
- Area of a square (A) vs. the side length of the square (s): A = s^2
- Perimeter of an equilateral triangle (P) vs. the side length of the triangle (s): 3s = P
- Length (L) vs. width (w) for a rectangle whose area is 60 square units: L = \frac{60}{w}
Problem 2
- Clare has $54 in her bank account. A store credits her account with a $10 refund. How much does she now have in the bank?
- Mai owes the bank $60. She gets $85 for her birthday and deposits it into her account. How much does she now have in the bank?
- Tyler is overdrawn at the bank by $180. His brother has $70 more than him. How much money does Tyler’s brother have?
- Andre has $37 in his bank account and writes a check for $87. After the check has been cashed, what will the bank balance show?
Problem 3 (from Unit 4, Lesson 8)
Last week, it rained x inches. This week, the amount of rain decreased by 5%. Which expressions represent the amount of rain that fell this week? Select all that apply.
- g - 0.05
- g - 0.05g
- 0.95g
- 0.05g
- (1-0.05)g
Problem 4
The table shows five transactions and the resulting account balance in a bank account, except some numbers are missing. Fill in the missing numbers.
| transaction amount | account balance | |
|---|---|---|
| transaction 1 | 200 | 200 |
| transaction 2 | -147 | 53 |
| transaction 3 | 90 | |
| transaction 4 | -229 | |
| transaction 5 | 0 |
Problem 5 (from Unit 5, Lesson 3)
Add.
- 5\frac34 + (\text{-}\frac {1}{4})
- \text {-}\frac {2}{3} + \frac16
- \text{-}\frac {8}{5} + (\text{-}\frac {3}{4})
Problem 6 (from Unit 5, Lesson 1)
In each diagram, x represents a different value. For each diagram,
-
What is something that is definitely true about the value of x?
-
What is something that could be true about the value of x?

Lesson 5
Problem 1
Write each subtraction equation as an addition equation.
- a-9 = 6
- p-20=\text-30
- z-(\text-12)=15
- x-(\text-7)=\text-10
Problem 2
Find each difference. If you get stuck, consider drawing a number line diagram.
-
9 - 4
-
4 - 9
-
9 - (\text-4)
-
\text-9 - (\text-4)
-
\text-9 - 4
-
4 - (\text-9)
-
\text-4 - (\text-9)
-
\text-4 - 9
Problem 3 (from Unit 4, Lesson 10)
Problem 4
Find the solution to each equation mentally.
- 30+a=40
- 500+b=200
- \text-1+c=\text-2
- d+3,\!567=0
Problem 5 (from Unit 2, Lesson 3)
One kilogram is 2.2 pounds. Complete the tables. What is the interpretation of the constant of proportionality in each case?
| row 1 | pounds | kilograms |
|---|---|---|
| row 2 | 2.2 | 1 |
| row 3 | 11 | |
| row 4 | 5.5 | |
| row 5 | 1 |
______ kilogram per pound
| row 1 | kilograms | pounds |
|---|---|---|
| row 2 | 1 | 2.2 |
| row 3 | 7 | |
| row 4 | 30 | |
| row 5 | 0.5 |
______ pounds per kilogram
Lesson 6
Problem 1
Write a sentence to answer each question:
-
How much warmer is 82 than 40?
-
How much warmer is 82 than -40?
Problem 2 (from Unit 2, Lesson 8)
A company produces screens of different sizes. Based on the table, could there be a relationship between the number of pixels and the area of the screen? If so, write an equation representing the relationship. If not, explain your reasoning.
| square inches of screen | number of pixels | |
|---|---|---|
| row 1 | 6 | 31,104 |
| row 2 | 72 | 373,248 |
| row 3 | 105 | 544,320 |
| row 4 | 300 | 1,555,200 |
Problem 3
-
What is the difference in height between 30 m up a cliff and 87 m up a cliff? What is the distance between these positions?
-
What is the difference in height between an albatross flying at 100 m above the surface of the ocean and a shark swimming 30 m below the surface? What is the distance between them if the shark is right below the albatross?
Problem 4
Find each difference.
-
(\text-5) - 6
-
35 - (\text-8)
-
\frac25 - \frac35
-
\text-4\frac38 - (\text-1\frac14)
Problem 5 (from Unit 4, Lesson 10)
A family goes to a restaurant. When the bill comes, this is printed at the bottom of it:
| row 1 | Gratuity Guide For Your Convenience: 15% would be $4.89 18% would be $5.87 20% would be $6.52 |
|---|
How much was the price of the meal? Explain your reasoning.
Problem 6 (from Unit 1, Lesson 2)
Which is a scaled copy of Polygon A? Identify a pair of corresponding sides and a pair of corresponding angles. Compare the areas of the scaled copies.

Lesson 7
Problem 1 (from Unit 4, Lesson 10)
Tyler orders a meal that costs $15.
- If the tax rate is 6.6%, how much will the sales tax be on Tyler’s meal?
- Tyler also wants to leave a tip for the server. How much do you think he should pay in all? Explain your reasoning.
Problem 2 (from Unit 2, Lesson 3)
In a video game, a character is healed at a constant rate as long as they are standing in a certain circle. Complete the table.
| time in circle (seconds) |
health gained (points) |
|
|---|---|---|
| Row 1 | 4 | 100 |
| Row 2 | 10 | |
| Row 3 | 3 | |
| Row 4 | 1,000 |
Problem 3 (from Unit 5, Lesson 6)
- How much higher is 500 than 400 m?
- How much higher is 500 than -400 m?
- What is the change in elevation from 8,500 m to 3,400 m?
- What is the change in elevation between 8,500 m and -300 m?
- How much higher is -200 m than 450 m?
Problem 4
The table shows four transactions and the resulting account balance in a bank account, except some numbers are missing. Fill in the missing numbers.
| transaction amount | account balance | |
|---|---|---|
| transaction 1 | 360 | 360 |
| transaction 2 | -22.50 | 337.50 |
| transaction 3 | 182.35 | |
| transaction 4 | -41.40 |
Problem 5
The departure from the average is the difference between the actual amount of rain and the average amount of rain for a given month.
The historical average for rainfall in Albuquerque, NM for June, July, and August is shown in the table.
| June | July | August | |
|---|---|---|---|
| average rainfall (inches) | 0.67 | 1.5 | 1.57 |
- Last June only 0.17 inches of rain fell all month. What is the difference between the average rainfall and the actual rainfall for last June?
- The departure from the average rainfall last July was -0.36 inches. How much rain fell last July?
- How much rain would have to fall in August so that the total amount of rain equals the average rainfall for these three months? What would the departure from the average be in August in that situation?
Lesson 8
Problem 1
A number line can represent positions that are north and south of a truck stop on a highway. Decide whether you want positive positions to be north or south of the truck stop. Then plot the following positions on a number line.
- The truck stop
- 5 miles north of the truck stop
-
3.5 miles south of the truck stop
Problem 2
- How could you distinguish between traveling west at 5 miles per hour and traveling east at 5 miles per hour without using the words “east” and “west”?
- Four people are cycling. They each start at the same point. (0 represents their starting point.) Plot their finish points after five seconds of cycling on a number line
- Lin cycles at 5 meters per second
- Diego cycles at -4 meters per second
- Elena cycles at 3 meters per second
-
Noah cycles at -6 meters per second
Problem 3 (from Unit 5, Lesson 6)
Find the value of each expression.
16.2 + \text-8.4
\frac25 - \frac35
\text-9.2 + \text-7
(\text-4\frac38) - (\text-1\frac14)
Problem 4 (from Unit 4, Lesson 10)
A shopper bought a watermelon, a pack of napkins, and some paper plates. In his state, there is no tax on food. The tax rate on non-food items is 5%. The total for the three items he bought was $8.25 before tax, and he paid $0.19 in tax. How much did the watermelon cost?
Problem 5 (from Unit 5, Lesson 5)
For each equation, write two more equations using the same numbers that express the same relationship in a different way.
- 3 + 2 = 5
- 7.1 + 3.4 = 10.5
- 15 - 8 = 7
- \frac32 + \frac95 = \frac{33}{10}
Problem 6 (from Unit 2, Lesson 10)
Which graphs could not represent a proportional relationship? Explain how you decided.

Lesson 9
Problem 1
Fill in the missing numbers in these equations
- (\text-2) \boldcdot (\text-4.5) = {?}
- (\text-8.7) \boldcdot (\text-10) = {?}
- (\text-7) \boldcdot {?} = 14
- {?} \boldcdot (\text-10) = 90
Problem 2
A weather station on the top of a mountain reports that the temperature is currently 0^\circ\text{C} and has been falling at a constant rate of 3^\circ\text{C} per hour. Find each temperature. Explain or show your reasoning.
If it continues fall at this rate, what will the temperature be:
- in 2 hours?
- in 5 hours?
- in half an hour?
What was the temperature:
- 1 hour ago?
- 3 hours ago?
- 4.5 hours ago?
Problem 3
Find the value of each expression.
- \frac14 \boldcdot (\text-12)
- (\text{-}\frac {1}{3}) \boldcdot 39
- (\text{-}\frac {4}{5}) \boldcdot (\text-75)
- (\text{-}\frac {2}{5}) \boldcdot (\text{-}\frac {3}{4})
- \frac83 \boldcdot (\text-42)
Problem 4 (from Unit 4, Lesson 2)
To make a specific hair dye, a hair stylist uses a ratio of 1\frac18 oz of red tone, \frac 34 oz of gray tone, and \frac58 oz of brown tone.
-
If the stylist needs to make 20 oz of dye, how much of each dye color is needed?
-
If the stylist needs to make 100 oz of dye, how much of each dye color is needed?
Problem 5 (from Unit 5, Lesson 7)
- Here are the vertices of rectangle FROG: (\text-2,5), (\text-2,1), (6,5), (6,1). Find the perimeter of this rectangle. If you get stuck, try plotting the points on a coordinate plane.
- Find the area of the rectangle FROG.
- Here are the coordinates of rectangle PLAY: (\text-11, 20), (\text-11, \text-3), (\text-1, 20), (\text-1, \text-3). Find the perimeter and area of this rectangle. See if you can figure out its side lengths without plotting the points.
Lesson 10
Problem 1
Evaluate each expression:
- \text-12 \boldcdot \frac13
- \text-12 \boldcdot \left(\text{-}\frac {1}{3}\right)
- 12 \boldcdot \left(\text{-}\frac {5}{4}\right)
- \text-12 \boldcdot \left(\text{-}\frac {5}{4}\right)
Problem 2
Evaluate each expression:
- (\text-1) \boldcdot 2 \boldcdot 3
- (\text-1) \boldcdot (\text-2) \boldcdot 3
- (\text-1) \boldcdot (\text-2) \boldcdot (\text-3)
Problem 3 (from Unit 5, Lesson 1)
Order each set of numbers from least to greatest.
- 4, 8, -2, -6, 0
- -5, -5.2, 5.5, \text-5\frac12, \frac {\text{-}5}{2}
Problem 4 (from Unit 5, Lesson 3)
30 + \text-30 = 0.
- Write another sum of two numbers that equals 0.
- Write a sum of three numbers that equals 0.
- Write a sum of four numbers that equals 0, none of which are opposites.
Problem 5 (from Unit 5, Lesson 6)
A submarine is searching for underwater features. It is accompanied by a small aircraft and an underwater robotic vehicle.
At one time the aircraft is 200 m above the surface, the submarine is 55 m below the surface, and the underwater robotic vehicle is 227 m below the surface.
- What is the difference in height between the submarine and the aircraft?
- What is the distance between the underwater robotic vehicle and the submarine?
Problem 6 (from Unit 5, Lesson 8)
- Clare is cycling at a speed of 12 miles per hour. If she starts at a position chosen as zero, what will her position be after 45 minutes?
- Han is cycling at a speed of -8 miles per hour; if he starts at the same zero point, what will his position be after 45 minutes?
- What will the distance between them be after 45 minutes?
Problem 7 (from Unit 5, Lesson 9)
Fill in the missing numbers in these equations
- (\text-7)\boldcdot {?} = \text-14
- {?}\boldcdot 3 = \text-15
- {?}\boldcdot 4 = 32
- \text-49 \boldcdot 3 ={?}
Lesson 11
Problem 1
Find the quotients:
24 \div \text-6
\text-15 \div 0.3
\text-4 \div \text-20
Problem 2
Find the quotients.
- \frac25 \div \frac34
- \frac94 \div \frac {\text{-}3}{4}
- \frac {\text{-}5}{7} \div \frac {\text{-}1}{3}
- \frac {\text{-}5}{3} \div \frac16
Problem 3
Is the solution positive or negative?
- 2\boldcdot x=6
- \text-2\boldcdot x=6.1
- 2.9 \boldcdot x = \text-6.04
- \text-2.473\boldcdot x = \text-6.859
Problem 4
Find the solution mentally.
- 3 \boldcdot (\text-4) = a
- b \boldcdot (\text-3) = \text-12
- (\text- 12) \boldcdot c = 12
- d \boldcdot 24 = \text-12
Problem 5 (from Unit 4, Lesson 2)
In order to make a specific shade of green paint, a painter mixes 1\frac12 quarts of blue paint, 2 cups of green paint, and \frac12 gallon of white paint. How much of each color is needed to make 100 cups of this shade of green paint?
Problem 6 (from Unit 5, Lesson 3)
Here is a list of the highest and lowest elevation on each continent.
| highest point (m) | lowest point (m) | |
|---|---|---|
| Europe | 4,810 | -28 |
| Asia | 8,848 | -427 |
| Africa | 5,895 | -155 |
| Australia | 4,884 | -15 |
| North America | 6,198 | -86 |
| South America | 6,960 | -105 |
| Antarctica | 4,892 | -50 |
- Which continent has the largest difference in elevation? The smallest?
- Make a display (dot plot, box plot, or histogram) of the data set and explain why you chose that type of display to represent this data set.
Lesson 12
Problem 1 (from Unit 4, Lesson 3)
- A cookie recipe uses 3 cups of flour to make 15 cookies. How many cookies can you make with this recipe with 4 cups of flour? (Assume you have enough of the other ingredients.)
- A teacher uses 36 centimeters of tape to hang up 9 student projects. At that rate, how much tape would the teacher need to hang up 10 student projects?
Problem 2 (from Unit 5, Lesson 11)
Evaluate each expression. When the answer is not a whole number, write your answer as a fraction.
- \text-4 \boldcdot \text-6
- \text-24 \boldcdot \frac {\text{-}7}{6}
- 4 \div \text-6
- \frac43 \div \text-24
Problem 3
Some boats were traveling up and down a river. A satellite recorded the movements of several boats.
- A motor boat traveled -3.4 miles per hour for 0.75 hours. How far did it go?
- A tugboat traveled -1.5 miles in 0.3 hours. What was its velocity?
- What do you think that negative distances and velocities could mean in this situation?
Problem 4
Describe a situation where each of the following quantities might be useful.
- -20 gallons per hour
- -10 feet per minute
- -0.1 kilograms per second
Problem 5
A submarine is only allowed to change its depth by rising toward the surface in 60-meter stages. It starts off at -340 meters.
-
At what depth is it after:
- 1 stage
- 2 stages
- 4 stages
- How many stages will it take to return to the surface?
Lesson 13
Problem 1 (from Unit 4, Lesson 3)
- A coffee maker’s directions say to use 2 tablespoons of ground coffee for every 6 ounces of water. How much coffee should you use for 33 ounces of water?
- A runner is running a 10 km race. It takes her 17.5 minutes to reach the 2.5 km mark. At that rate, how long will it take her to run the whole race?
Problem 2 (from Unit 4, Lesson 10)
The price of an ice cream cone is $3.25, but it costs $3.51 with tax. What is the sales tax rate?
Problem 3
Find the value of each expression.
- \text-22 + 5
- \text-22 - (\text-5)
- (\text-22) (\text-5)
- (\text-22) \div 5
Problem 4 (from Unit 4, Lesson 7)
Two students are both working on the same problem: A box of laundry soap has 25% more soap in its new box. The new box holds 2 kg. How much soap did the old box hold?
- Here is how Jada set up her double number line.
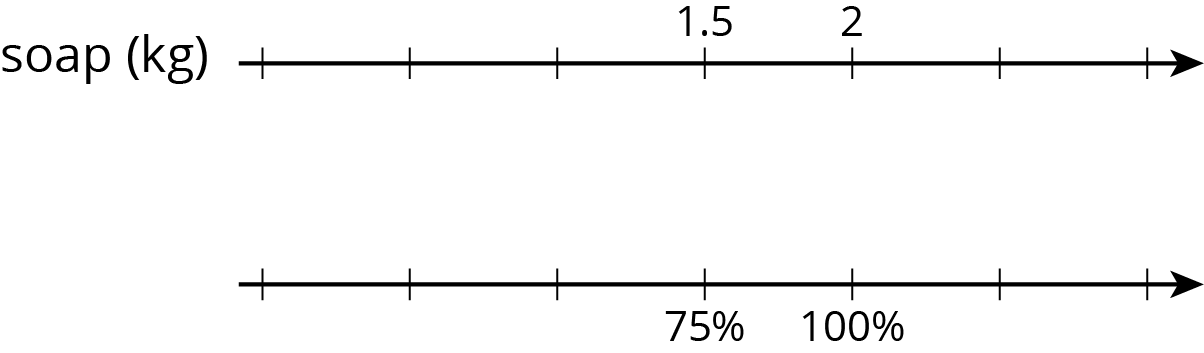
- Here is how Lin set up her double number line.
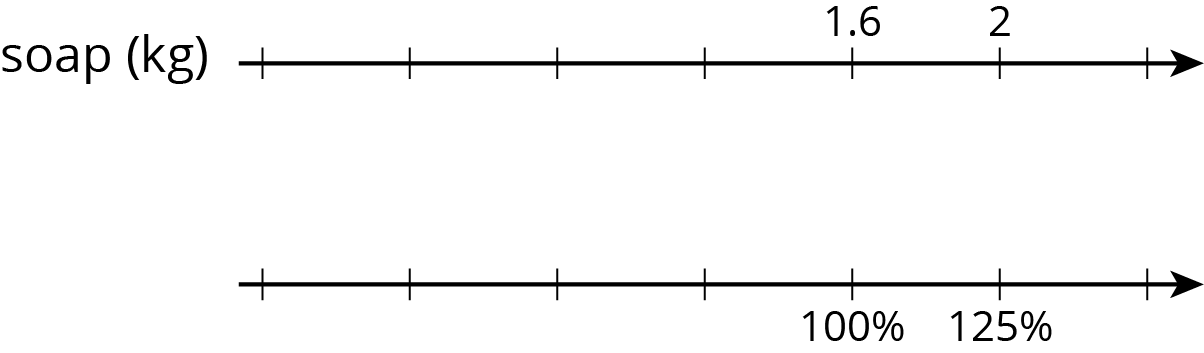
Do you agree with either of them? Explain or show your reasoning.
Problem 5
The value of x is \frac {\text{-}1}{4}. Order these expressions from least to greatest:
x
1-x
x-1
\text-1\div x
Problem 6
Here are four expressions that have the value \frac {\text{-}1}{2}:
\frac {\text{-}1}{4} + (\frac {\text{-}1}{4})
\frac12 - 1
\text-2 \boldcdot \frac14
\text-1 \div 2
Write five expressions: a sum, a difference, a product, a quotient, and one that involves at least two operations that have the value \frac {\text{-}3}{4}.
Lesson 14
Problem 1 (from Unit 4, Lesson 11)
A furniture store pays a wholesale price for a mattress. Then, the store marks up the retail price to 150% of the wholesale price. Later, they put the mattress on sale for 50% off of the retail price. A customer just bought the mattress on sale and paid $1,200.
- What was the retail price of the mattress, before the discount?
- What was the wholesale price, before the markup?
Problem 2
The table shows transactions in a checking account.
| January | |
|---|---|
| row 1 | -38.50 |
| row 2 | 126.30 |
| row 3 | 429.40 |
| row 4 | -265.00 |
| February | |
|---|---|
| row 1 | 250.00 |
| row 2 | -135.20 |
| row 3 | 35.50 |
| row 4 | -62.30 |
| March | |
|---|---|
| row 1 | -14.00 |
| row 2 | 99.90 |
| row 3 | -82.70 |
| row 4 | -1.50 |
| April | |
|---|---|
| row 1 | -86.80 |
| row 2 | -570.00 |
| row 3 | 100.00 |
| row 4 | -280.10 |
- Find the total of the transactions for each month.
- Find the mean total for the four months.
Problem 3
A bank charges a service fee of $7.50 per month for a checking account.
A bank account has $85.00. If no money is deposited or withdrawn except the service charge, how many months until the account balance is negative?
Problem 4
A large aquarium of water is being filled with a hose. Due to a problem, the sensor does not start working until some time into the filling process. The sensor starts its recording at the time zero minutes. The sensor initially detects the tank has 225 liters of water in it.
-
The hose fills the aquarium at a constant rate of 15 liters per minute. What will the sensor read at the time 5 minutes?
-
Later, someone wants to use the data to find the amount of water at times before the sensor started. What should the sensor have read at the time -7 minutes?
Problem 5 (from Unit 4, Lesson 10)
- A restaurant bill is $21. You leave a 15% tip. How much do you pay including the tip?
-
Which of the following represents the amount a customer pays including the tip of 15% if the bill was b dollars? Select all that apply.
- 0.15b
- 15b
- b+0.15b
- 1.15b
- 1.015b
- b+\frac{15}{100}b
- b+0.15
Lesson 15
Problem 1
Solve.
-
\frac25t=6
-
\text-4.5 = a-8
-
\frac12+p= \text-3
-
12=x \boldcdot 3
-
\text-12 = \text-3y
Problem 2 (from Unit 5, Lesson 13)
Evaluate each expression if x is \frac{2}{5}, y is \text-4, and z is -0.2.
-
x+y
-
2x-z
-
x+y+z
-
y \boldcdot x
Problem 3
Match each equation to a step that will help solve the equation.
- 5x=0.4
- \frac{x}{5}=8
- 3=\frac {\text{-}x}{5}
- 7=\text-5x
- Multiply each side by 5.
- Multiply each side by -5.
- Multiply each side by \frac15.
- Multiply each side by \frac {\text{-}1}{5}.
Problem 4
- Write an equation where a number is added to a variable, and a solution is -8.
- Write an equation where a number is multiplied by a variable, and a solution is \frac {\text{-}4}{5}.
Problem 5 (from Unit 5, Lesson 8)
The markings on the number line are evenly spaced. Label the other markings on the number line.

Problem 6 (from Unit 5, Lesson 12)
In 2012, James Cameron descended to the bottom of Challenger Deep in the Marianas Trench; the deepest point in the ocean. The vessel he rode in was called DeepSea Challenger.
Challenger Deep is 35,814 feet deep at its lowest point
- DeepSea Challenger’s descent was a change in depth of (\text-4) feet per second. We can use the equation y=\text-4x to model this relationship, where y is the depth and x is the time in seconds that have passed. How many seconds does this model suggest it would take for DeepSea Challenger to reach the bottom?
- To end the mission DeepSea Challenger made a one-hour ascent to the surface. How many seconds is this?
- The ascent can be modeled by a different proportional relationship y=kx. What is the value of k in this case?
Lesson 16
Problem 1
Match each situation to one of the equations.
- A whale was diving at a rate of 2 meters per second. How long will it take for the whale to get from the surface of the ocean to an elevation of -12 meters at that rate?
- A swimmer dove below the surface of the ocean. After 2 minutes, she was 12 meters below the surface. At what rate was she diving?
- The temperature was -12 degrees Celsius and rose to 2 degrees Celsius. What was the change in temperature?
- The temperature was 2 degrees Celsius and fell to -12 degrees Celsius. What was the change in temperature?
- \text-12 + x = 2
- 2 + x = \text-12
- \text-2x = \text-12
- 2x = \text-12
Problem 2
Starting at noon, the temperature dropped steadily at a rate of 0.8 degrees Celsius every hour.
For each of these situations, write and solve an equation and describe what your variable represents.
-
How many hours did it take for the temperature to decrease by 4.4 degrees Celsius?
-
If the temperature after the 4.4 degree drop was -2.5 degrees Celsius, what was the temperature at noon?
Problem 3 (from Unit 4, Lesson 3)
Kiran mixes \frac34 cups of raisins, 1 cup peanuts, and \frac12 cups of chocolate chips to make trail mix. How much of each ingredient would he need to make 10 cups of trail mix? Explain your reasoning.
Problem 4 (from Unit 5, Lesson 6)
Find the value of each expression.
- 12 + (\text-10)
- (\text-5) - 6
- (\text-42) + 17
- 35 - (\text-8)
- (\text-4\frac12) + 3
Problem 5 (from Unit 5, Lesson 8)
The markings on the number line are evenly spaced. Label the other markings on the number line.

Problem 6
Kiran drinks 6.4 oz of milk each morning. How many days does it take him to finish a 32 oz container of milk?
-
Write and solve an equation for the situation.
-
What does the variable represent?
Lesson 17
No practice problems for this lesson.