12.1: Tax, Tip, and Discount
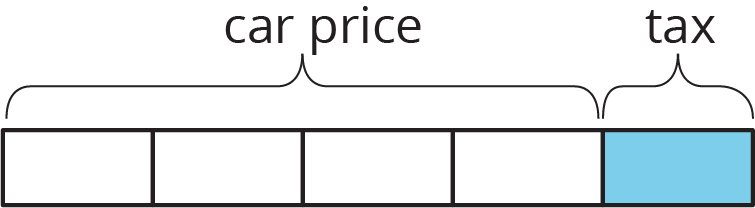
What percentage of the car price is the tax?
What percentage of the food cost is the tip?

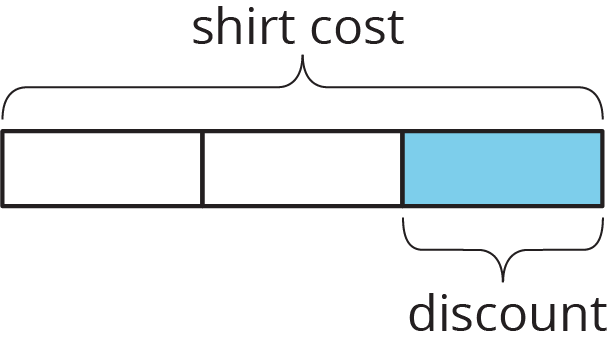
What percentage of the shirt cost is the discount?
Let’s find unknown percentages.
What percentage of the car price is the tax?

What percentage of the food cost is the tip?

What percentage of the shirt cost is the discount?

To make a Koch snowflake,

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
If your teacher gives you the data card:
To find a 30% increase over 50, we can find 130% of 50.
1.3 \boldcdot 50 = 65
To find a 30% decrease from 50, we can find 70% of 50.
0.7 \boldcdot 50 = 35
If we know the initial amount and the final amount, we can also find the percent increase or percent decrease. For example, a plant was 12 inches tall and grew to be 15 inches tall. What percent increase is this? Here are two ways to solve this problem:
The plant grew 3 inches, because 15 - 12=3. We can divide this growth by the original height, 3 \div 12 = 0.25. So the height of the plant increased by 25%.
The plant's new height is 125% of the original height, because 15 \div 12=1.25. This means the height increased by 25%, because 125 - 100 = 25.
Here are two ways to solve the problem: A rope was 2.4 meters long. Someone cut it down to 1.9 meters. What percent decrease is this?
The rope is now 2.4 - 1.9, or 0.5 meters shorter. We can divide this decrease by the original length, 0.5 \div 2.4 = 0.208\overline3. So the length of the rope decreased by approximately 20.8%.
The rope's new length is about 79.2% of the original length, because 1.9 \div 2.4 = 0.791\overline6. The length decreased by approximately 20.8%, because 100 - 79.2 = 20.8.