1.1: Using the Thermometer
Here is a weather thermometer. Three of the numbers have been left off.
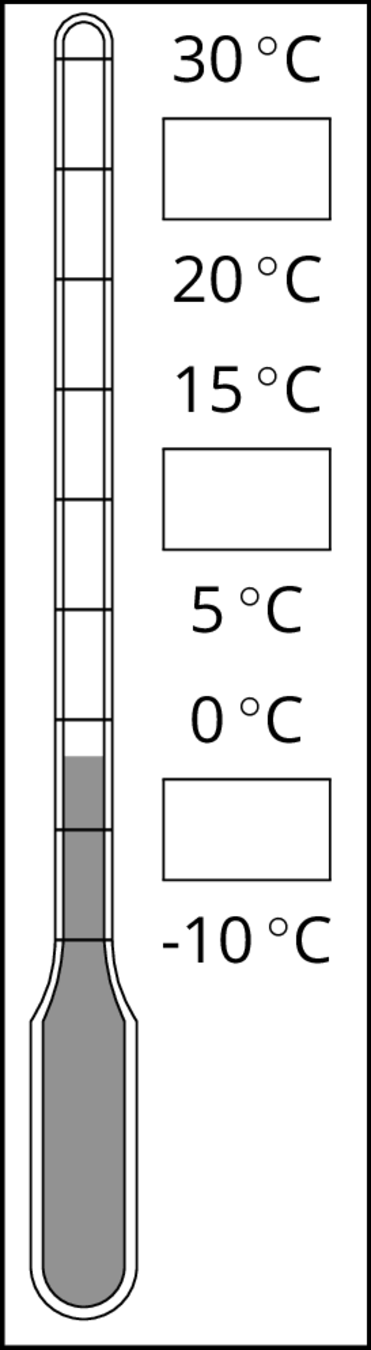
- What numbers go in the boxes?
- What temperature does the thermometer show?
Let's review what we know about signed numbers.
Here is a weather thermometer. Three of the numbers have been left off.

What temperature is shown on each thermometer?
Suppose the temperature outside is \text{-}4^\circ \text{C}. Is that colder or warmer than the coldest temperature shown? How do you know?

Here is a picture of some sea animals. The number line on the left shows the vertical position of each animal above or below sea level, in meters.

How far above or below sea level is each animal? Measure to their eye level.
A mobula ray is 3 meters above the surface of the ocean. How does its distance from the surface of the ocean compare to the vertical distance from the eyes of:
The jumping dolphin?
The flying seagull?
The octopus?
An albatross is 5 meters above the surface of the ocean. How does its distance from the surface compare to the vertical distance from the eyes of:
The jumping dolphin?
The flying seagull?
The octopus?
A clownfish is 2 meters below the surface of the ocean. How does its distance from the surface compare to the vertical distance from the eyes of:
The jumping dolphin?
The flying seagull?
The octopus?
The vertical distance of a new dolphin from the dolphin in the picture is 3 meters. What is its distance from the surface of the ocean?
We can use positive and negative numbers to represent temperature and elevation.
When numbers represent temperatures, positive numbers indicate temperatures that are warmer than zero and negative numbers indicate temperatures that are colder than zero. This thermometer shows a temperature of -1 degree Celsius, which we write \text{-}1^\circ \text{C}.

When numbers represent elevations, positive numbers indicate positions above sea level and negative numbers indicate positions below sea level.
We can see the order of signed numbers on a number line.
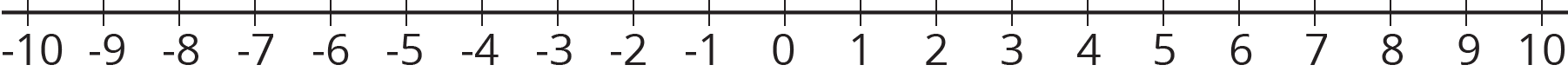
A number is always less than numbers to its right. So \text{-}7 < \text{-}3.
We use absolute value to describe how far a number is from 0. The numbers 15 and -15 are both 15 units from 0, so |15| = 15 and | \text{-}15| = 15. We call 15 and -15 opposites. They are on opposite sides of 0 on the number line, but the same distance from 0.