Objects
- A person
- A football field (120 yards by 53\frac{1}{3} yards)
- The state of Washington (about 240 miles by 360 miles)
- The floor plan of a house
- A rectangular farm (6 miles by 2 mile)
Which one of these shapes is not like the others? Explain what makes it different by representing each width and height pair with a ratio.

For each object, choose an appropriate scale for a drawing that fits on a regular sheet of paper. Not all of the scales on the list will be used.
Objects
Scales
Which scale is equivalent to 1 cm to 1 km?
When Han makes chocolate milk, he mixes 2 cups of milk with 3 tablespoons of chocolate syrup. Here is a table that shows how to make batches of different sizes.
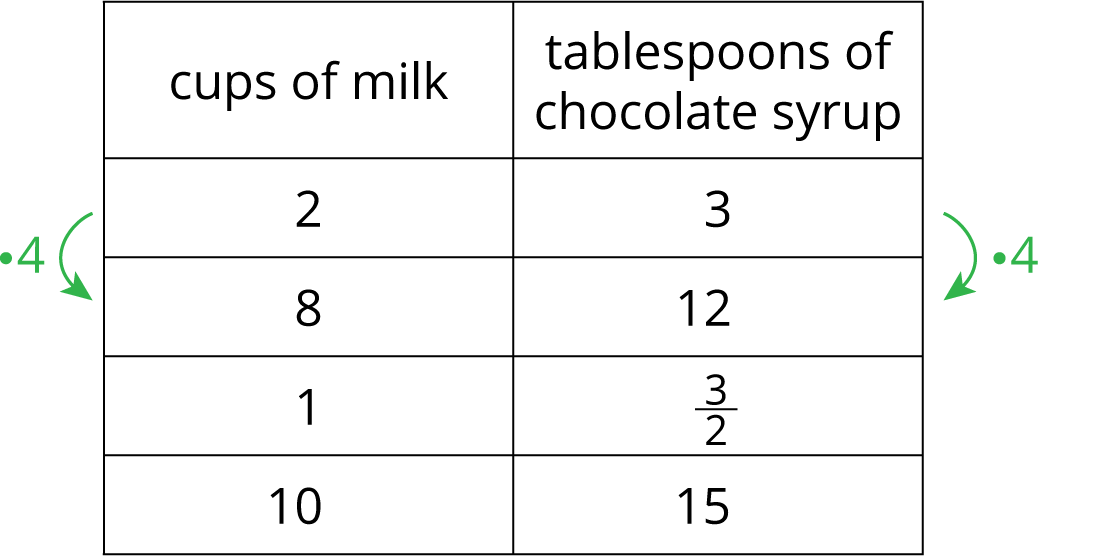
Use the information in the table to complete the statements. Some terms are used more than once.
Bank of Terms: tablespoons of chocolate syrup, 4, cups of milk, cup of milk, \frac32
A certain shade of pink is created by adding 3 cups of red paint to 7 cups of white paint.
| cups of white paint | cups of red paint | |
|---|---|---|
| Row 1 | 1 | |
| Row 2 | 7 | 3 |
A map of a rectangular park has a length of 4 inches and a width of 6 inches. It uses a scale of 1 inch for every 30 miles.
What is the actual area of the park? Show how you know.
The map needs to be reproduced at a different scale so that it has an area of 6 square inches and can fit in a brochure. At what scale should the map be reproduced so that it fits on the brochure? Show your reasoning.
Noah drew a scaled copy of Polygon P and labeled it Polygon Q.

If the area of Polygon P is 5 square units, what scale factor did Noah apply to Polygon P to create Polygon Q? Explain or show how you know.
Select all the ratios that are equivalent to each other.
Noah is running a portion of a marathon at a constant speed of 6 miles per hour.
Complete the table to predict how long it would take him to run different distances at that speed, and how far he would run in different time intervals.
| row 1 | time in hours |
miles traveled at 6 miles per hour |
|---|---|---|
| row 2 | 1 | |
| row 3 | \frac12 | |
| row 4 | 1\frac13 | |
| row 5 | 1\frac12 | |
| row 6 | 9 | |
| row 7 | 4\frac12 |
One kilometer is 1000 meters.
| row 1 | meters | kilometers |
|---|---|---|
| row 2 | 1,000 | 1 |
| row 3 | 250 | |
| row 4 | 12 | |
| row 5 | 1 |
| row 1 | kilometers | meters |
|---|---|---|
| row 2 | 1 | 1,000 |
| row 3 | 5 | |
| row 4 | 20 | |
| row 5 | 0.3 |
The constant of proportionality tells us that:
The constant of proportionality tells us that:
Jada and Lin are comparing inches and feet. Jada says that the constant of proportionality is 12. Lin says it is \frac{1}{12}. Do you agree with either of them? Explain your reasoning.
The area of the Mojave desert is 25,000 square miles. A scale drawing of the Mojave desert has an area of 10 square inches. What is the scale of the map?
Which of these scales is equivalent to the scale 1 cm to 5 km? Select all that apply.
3 cm to 15 km
1 mm to 150 km
5 cm to 1 km
5 mm to 2.5 km
1 mm to 500 m
Which one of these pictures is not like the others? Explain what makes it different using ratios.

A certain ceiling is made up of tiles. Every square meter of ceiling requires 10.75 tiles. Fill in the table with the missing values.
| square meters of ceiling | number of tiles | |
|---|---|---|
| row 1 | 1 | |
| row 2 | 10 | |
| row 3 | 100 | |
| row 4 | a |
On a flight from New York to London, an airplane travels at a constant speed. An equation relating the distance traveled in miles, d, to the number of hours flying, t, is t = \frac{1}{500} d. How long will it take the airplane to travel 800 miles?
Each table represents a proportional relationship. For each, find the constant of proportionality, and write an equation that represents the relationship.
| s | P | |
|---|---|---|
| row 1 | 2 | 8 |
| row 2 | 3 | 12 |
| row 3 | 5 | 20 |
| row 4 | 10 | 40 |
Constant of proportionality:
Equation: P =
| d | C | |
|---|---|---|
| row 1 | 2 | 6.28 |
| row 2 | 3 | 9.42 |
| row 3 | 5 | 15.7 |
| row 4 | 10 | 31.4 |
Constant of proportionality:
Equation: C =
A map of Colorado says that the scale is 1 inch to 20 miles or 1 to 1,267,200. Are these two ways of reporting the scale the same? Explain your reasoning.
Here is a polygon on a grid.

Draw a scaled copy of the polygon using a scale factor 3. Label the copy A.
Draw a scaled copy of the polygon with a scale factor \frac{1}{2}. Label it B.
Is Polygon A a scaled copy of Polygon B? If so, what is the scale factor that takes B to A?
The table represents the relationship between a length measured in meters and the same length measured in kilometers.
| meters | kilometers | |
|---|---|---|
| row 1 | 1,000 | 1 |
| row 2 | 3,500 | |
| row 3 | 500 | |
| row 4 | 75 | |
| row 5 | 1 | |
| row 6 | x |
Concrete building blocks weigh 28 pounds each. Using b for the number of concrete blocks and w for the weight, write two equations that relate the two variables. One equation should begin with w = and the other should begin with b =.
A store sells rope by the meter. The equation p = 0.8L represents the price p (in dollars) of a piece of nylon rope that is L meters long.
The table represents a proportional relationship. Find the constant of proportionality and write an equation to represent the relationship.
| a | y | |
|---|---|---|
| row 1 | 2 | \frac23 |
| row 2 | 3 | 1 |
| row 3 | 10 | \frac{10}{3} |
| row 4 | 12 | 4 |
Constant of proportionality: __________
Equation: y =
On a map of Chicago, 1 cm represents 100 m. Select all statements that express the same scale.
5 cm on the map represents 50 m in Chicago.
1 mm on the map represents 10 m in Chicago.
1 km in Chicago is represented by 10 cm the map.
100 cm in Chicago is represented by 1 m on the map.
A car is traveling down a highway at a constant speed, described by the equation d = 65t, where d represents the distance, in miles, that the car travels at this speed in t hours.
Elena has some bottles of water that each holds 17 fluid ounces.
In Canadian coins, 16 quarters is equal in value to 2 toonies.
| number of quarters | number of toonies | |
|---|---|---|
| row 1 | 1 | |
| row 2 | 16 | 2 |
| row 3 | 20 | |
| row 4 | 24 |
Each table represents a proportional relationship. For each table:
| row 1 | x | y |
|---|---|---|
| row 2 | 2 | 10 |
| row 3 | 15 | |
| row 4 | 7 | |
| row 5 | 1 |
| row 1 | a | b |
|---|---|---|
| row 2 | 12 | 3 |
| row 3 | 20 | |
| row 4 | 10 | |
| row 5 | 1 |
| row 1 | m | n |
|---|---|---|
| row 2 | 5 | 3 |
| row 3 | 10 | |
| row 4 | 18 | |
| row 5 | 1 |
Describe some things you could notice in two polygons that would help you decide that they were not scaled copies.
Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would the constant of proportionality be?
| row 1 | distance to listener (ft) |
sound level (dB) |
|---|---|---|
| row 2 | 5 | 85 |
| row 3 | 10 | 79 |
| row 4 | 20 | 73 |
| row 5 | 40 | 67 |
| row 1 | volume (fluid ounces) |
cost ($) |
|---|---|---|
| row 2 | 16 | $1.49 |
| row 3 | 20 | $1.59 |
| row 4 | 30 | $1.89 |
A taxi service charges $1.00 for the first \frac{1}{10} mile then $0.10 for each additional \frac{1}{10} mile after that.
Fill in the table with the missing information then determine if this relationship between distance traveled and price of the trip is a proportional relationship.
| distance traveled (mi) | price (dollars) | |
|---|---|---|
| row 1 | \frac{9}{10} | |
| row 2 | 2 | |
| row 3 | 3\frac{1}{10} | |
| row 4 | 10 |
A rabbit and turtle are in a race. Is the relationship between distance traveled and time proportional for either one? If so, write an equation that represents the relationship.
Turtle’s run:
| distance (meters) | time (minutes) | |
|---|---|---|
| row 1 | 108 | 2 |
| row 2 | 405 | 7.5 |
| row 3 | 540 | 10 |
| row 4 | 1,768.5 | 32.75 |
Rabbit’s run:
| distance (meters) | time (minutes) | |
|---|---|---|
| row 1 | 800 | 1 |
| row 2 | 900 | 5 |
| row 3 | 1,107.5 | 20 |
| row 4 | 1,524 | 32.5 |
For each table, answer: What is the constant of proportionality?
| row 1 | a | b |
|---|---|---|
| row 2 | 2 | 14 |
| row 3 | 5 | 35 |
| row 4 | 9 | 63 |
| row 5 | \frac13 | \frac73 |
| row 1 | a | b |
|---|---|---|
| row 2 | 3 | 360 |
| row 3 | 5 | 600 |
| row 4 | 8 | 960 |
| row 5 | 12 | 1440 |
| row 1 | a | b |
|---|---|---|
| row 2 | 75 | 3 |
| row 3 | 200 | 8 |
| row 4 | 1525 | 61 |
| row 5 | 10 | 0.4 |
| row 1 | a | b |
|---|---|---|
| row 2 | 4 | 10 |
| row 3 | 6 | 15 |
| row 4 | 22 | 55 |
| row 5 | 3 | 7\frac12 |
Kiran and Mai are standing at one corner of a rectangular field of grass looking at the diagonally opposite corner. Kiran says that if the the field were twice as long and twice as wide, then it would be twice the distance to the far corner. Mai says that it would be more than twice as far, since the diagonal is even longer than the side lengths. Do you agree with either of them?
The relationship between a distance in yards (y) and the same distance in miles (m) is described by the equation y = 1760m.
| row 1 | distance measured in miles | distance measured in yards |
|---|---|---|
| row 2 | 1 | |
| row 3 | 5 | |
| row 4 | 3,520 | |
| row 5 | 17,600 |
Decide whether or not each equation represents a proportional relationship.
Is y proportional to x and y? Explain why or why not.
| x | y | |
|---|---|---|
| row 1 | 2 | |
| row 2 | 3 | |
| row 3 | 6 |
Is y proportional to x and y? Explain why or why not.
| x | y | |
|---|---|---|
| row 1 | 1 | |
| row 2 | 2 | |
| row 3 | 4 |
To transmit information on the internet, large files are broken into packets of smaller sizes. Each packet has 1,500 bytes of information. An equation relating packets to bytes of information is given by b = 1,\!500p where p represents the number of packets and b represents the number of bytes of information.
For each situation, explain whether you think the relationship is proportional or not. Explain your reasoning.


Every package of a certain toy also includes 2 batteries.
b =
t =
Lin and her brother were born on the same date in different years. Lin was 5 years old when her brother was 2.
| row 1 | Lin's age | Her brother's age |
|---|---|---|
| row 2 | 5 | 2 |
| row 3 | 6 | |
| row 4 | 15 | |
| row 5 | 25 |
A student argues that y=\frac{x}{9} does not represent a proportional relationship between x and y because we need to multiply one variable by the same constant to get the other one and not divide it by a constant. Do you agree or disagree with this student?
Quadrilateral A has side lengths 3, 4, 5, and 6. Quadrilateral B is a scaled copy of Quadrilateral A with a scale factor of 2. Select all of the following that are side lengths of Quadrilateral B.
Which graphs could represent a proportional relationship? Explain how you decided.

A lemonade recipe calls for \frac14 cup of lemon juice for every cup of water.
| x | y | |
|---|---|---|
| row 1 | 1 | \frac14 |
| row 2 | 2 | \frac12 |
| row 3 | 3 | \frac34 |
| row 4 | 4 | 1 |
| row 5 | 5 | 1\frac14 |
| row 6 | 6 | 1\frac12 |
Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?
The sizes you can print a photo
| row 1 | width of photo (inches) | height of photo (inches) |
|---|---|---|
| row 2 | 2 | 3 |
| row 3 | 4 | 6 |
| row 4 | 5 | 7 |
| row 5 | 8 | 10 |
The distance from which a lighthouse is visible.
| row 1 | height of a lighthouse (feet) | distance it can be seen (miles) |
|---|---|---|
| row 2 | 20 | 6 |
| row 3 | 45 | 9 |
| row 4 | 70 | 11 |
| row 5 | 95 | 13 |
| row 6 | 150 | 16 |
Select all of the pieces of information that would tell you x and y have a proportional relationship. Let y represent the distance between a rock and a turtle's current position in meters and x represent the number of minutes the turtle has been moving.
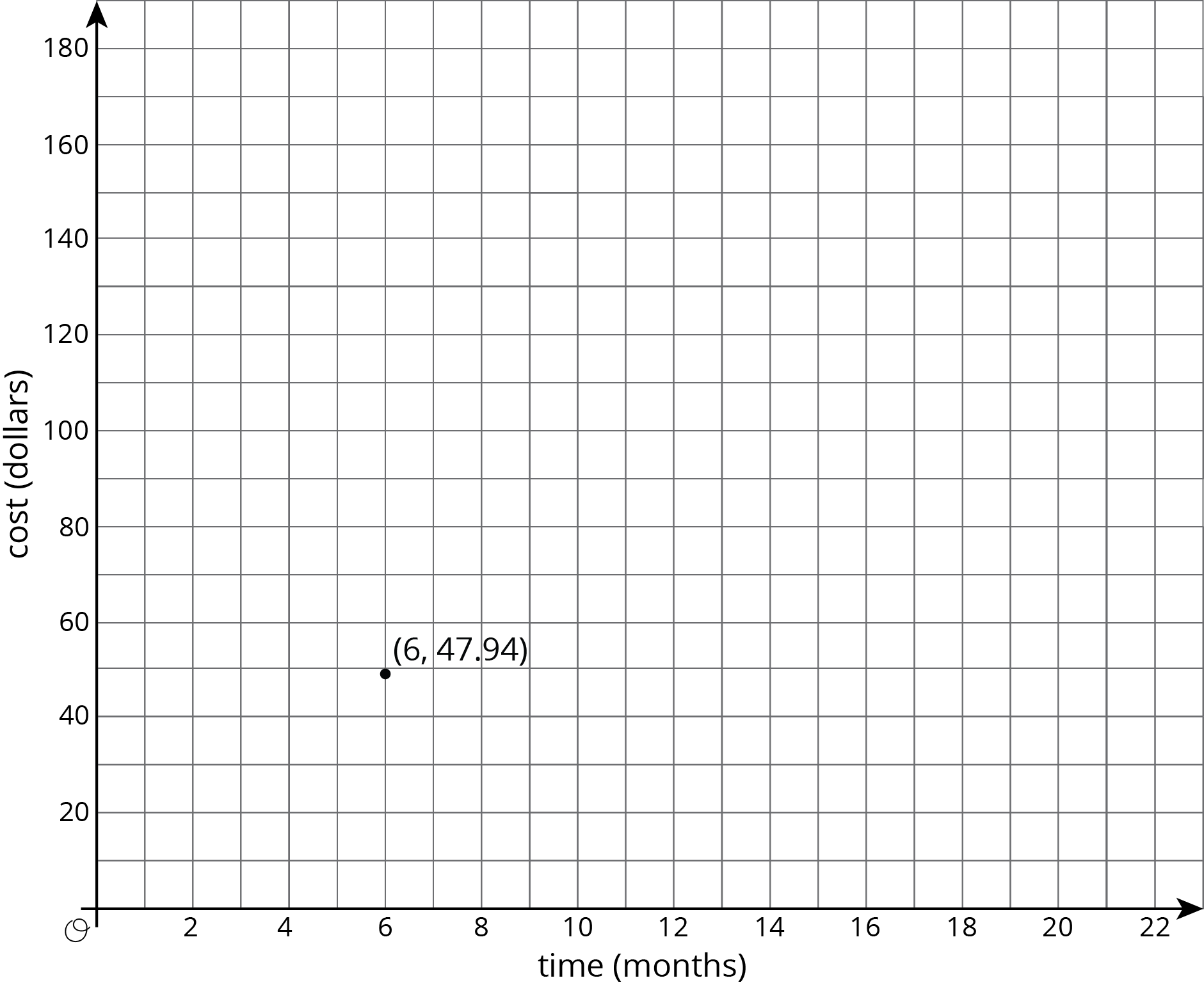
There is a proportional relationship between the number of months a person has had a streaming movie subscription and the total amount of money they have paid for the subscription. The cost for 6 months is $47.94. The point (6, 47.94) is shown on the graph below.
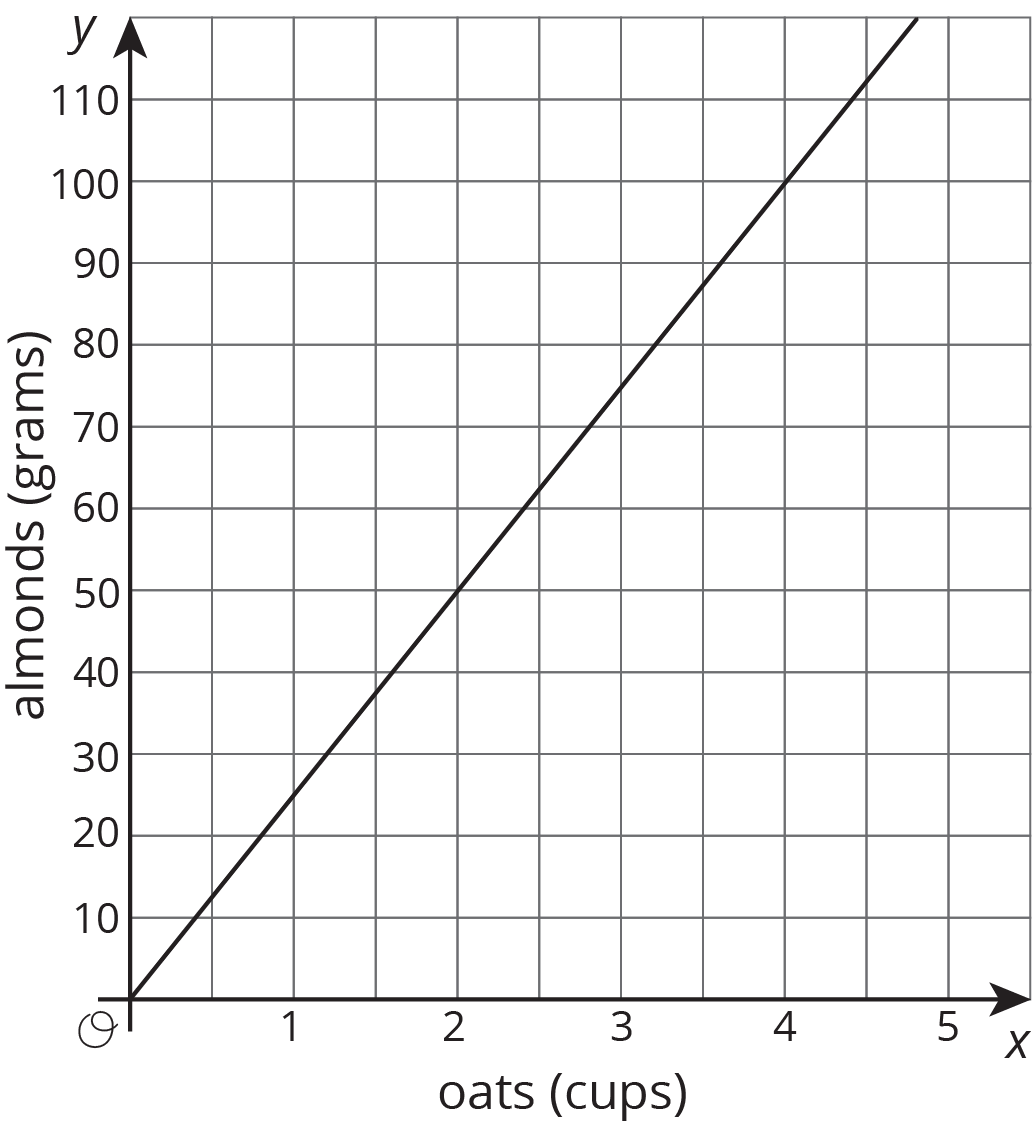
The graph shows the amounts of almonds, in grams, for different amounts of oats, in cups, in a granola mix. Label the point (1, k) on the graph, find the value of k, and explain its meaning.
To make a friendship bracelet, some long strings are lined up then taking one string and tying it in a knot with each of the other strings to create a row of knots. A new string is chosen and knotted with the all the other strings to create a second row. This process is repeated until there are enough rows to make a bracelet to fit around your friend's wrist.
Are the number of knots proportional to the number of rows? Explain your reasoning.
What information do you need to know to write an equation relating two quantities that have a proportional relationship?
Match each equation to its graph.
1
2
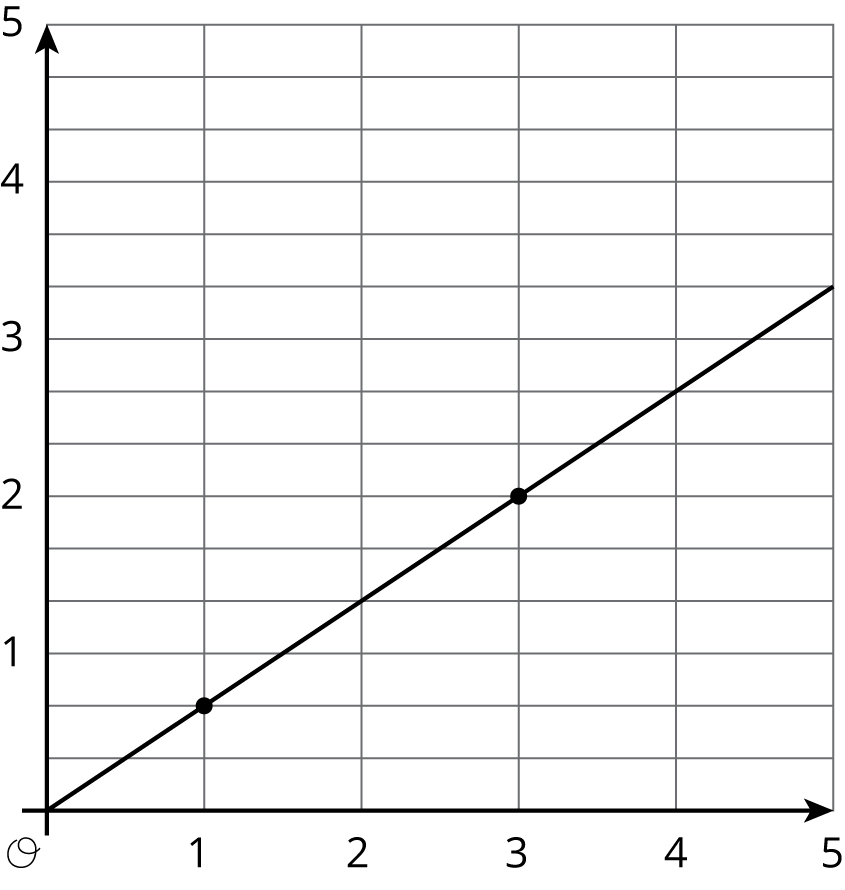
3
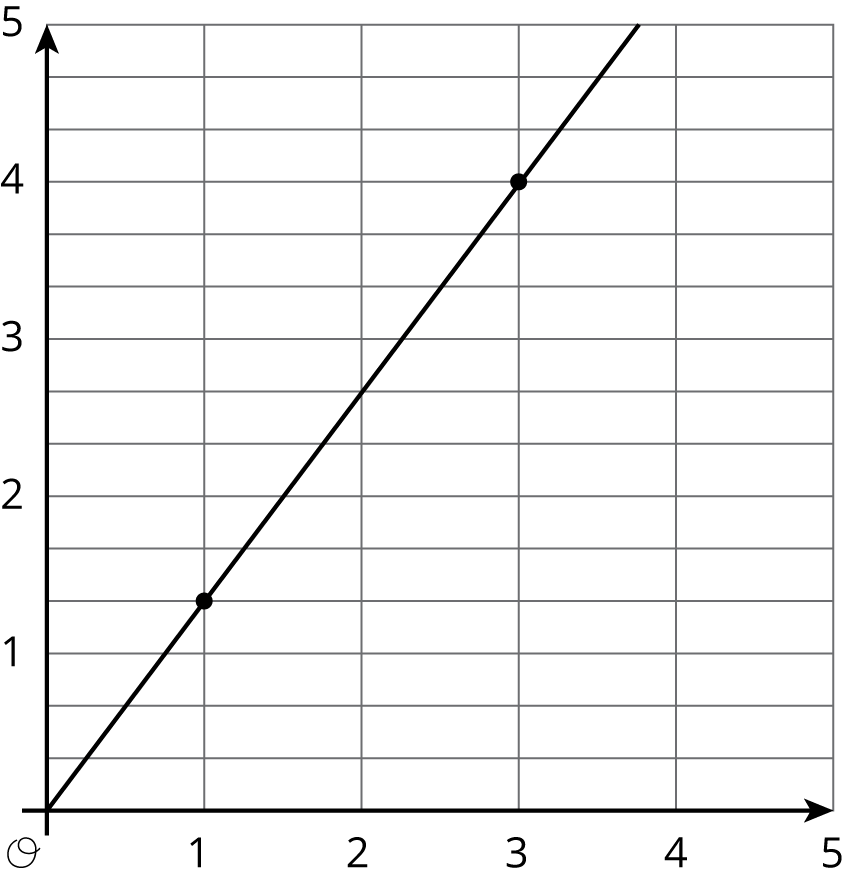
4
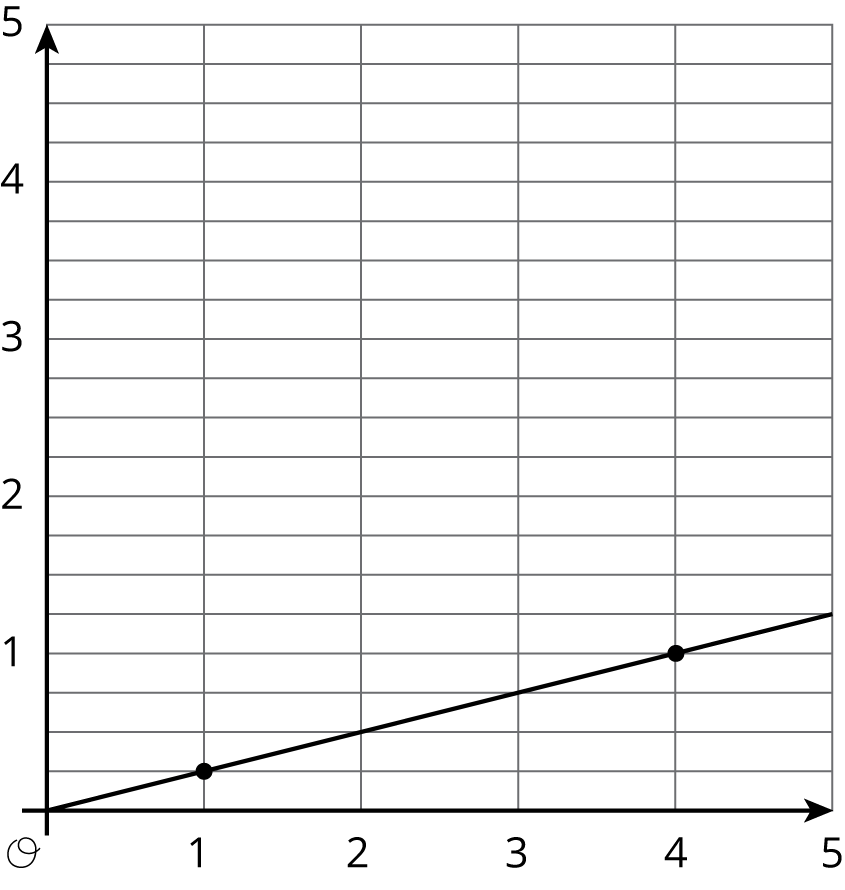
5
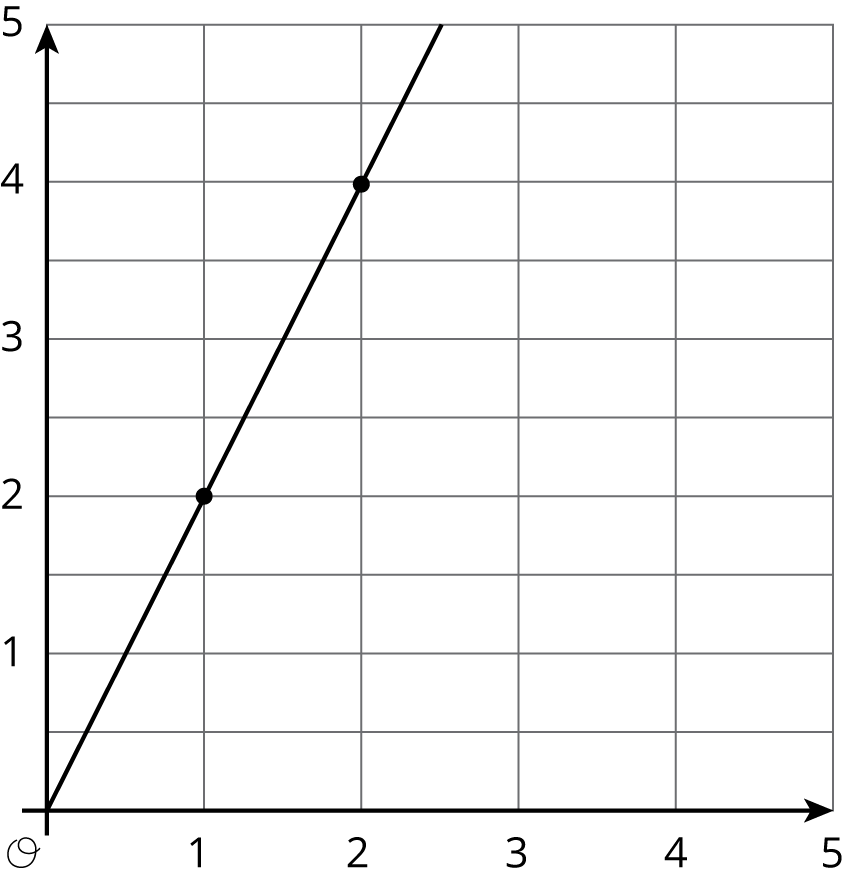
6
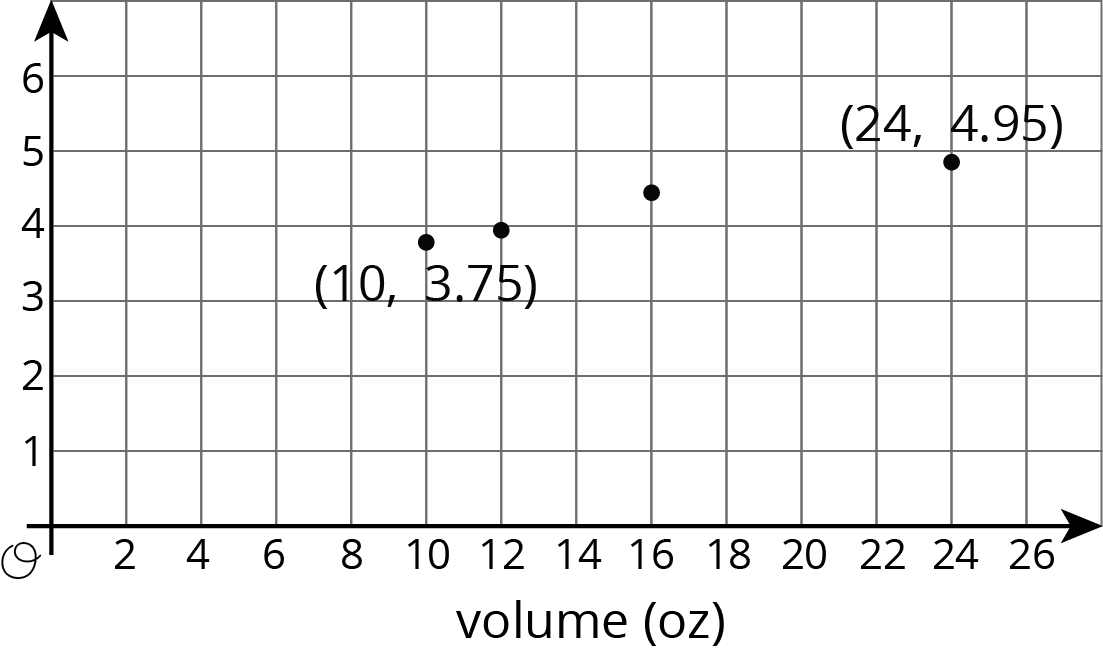
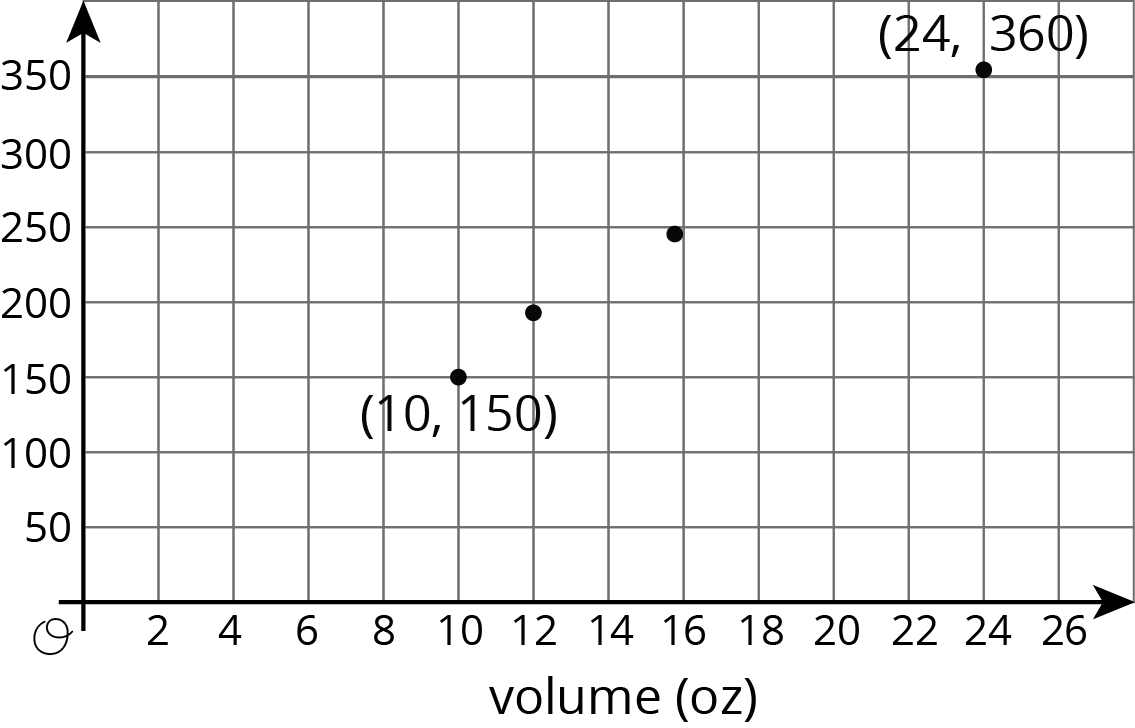
The graphs below show some data from a coffee shop menu. One of the graphs shows cost (in dollars) vs. drink volume (in ounces), and one of the graphs shows calories vs. drink volume (in ounces).
__________________ vs volume
_____________________ vs volume
Lin and Andre biked home from school at a steady pace. Lin biked 1.5 km and it took her 5 minutes. Andre biked 2 km and it took him 8 minutes.
At the supermarket you can fill your own honey bear container. A customer buys 12 oz of honey for $5.40.

The point (3, \frac65) lies on the graph representing a proportional relationship. Which of the following points also lie on the same graph? Select all that apply.
A trail mix recipe asks for 4 cups of raisins for every 6 cups of peanuts. There is proportional relationship between the amount of raisins, r (cups), and the amount of peanuts, p (cups), in this recipe.
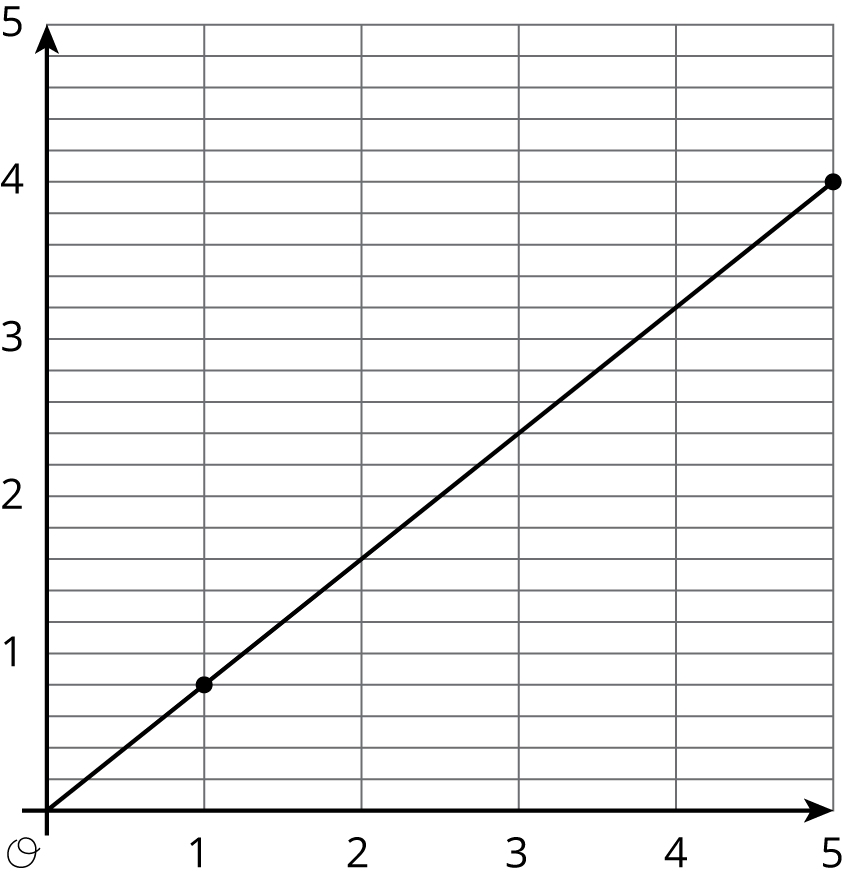
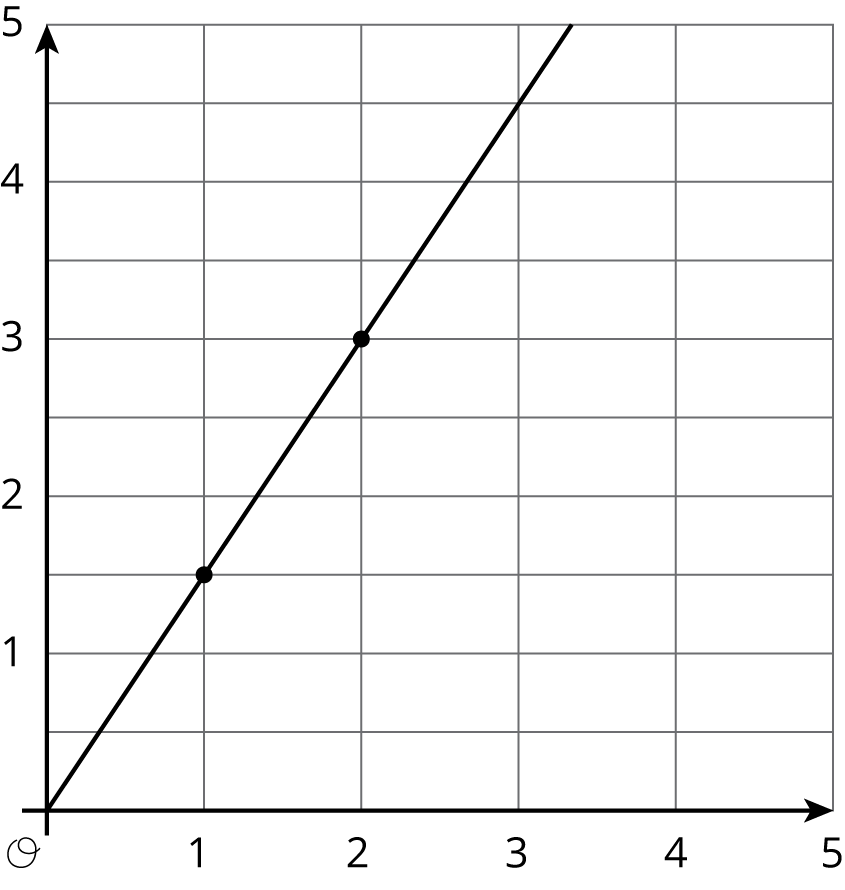
Here is a graph that represents a proportional relationship.

The equation c = 2.95g shows how much it costs to buy gas at a gas station on a certain day. In the equation, c represents the cost in dollars, and g represents how many gallons of gas were purchased.
There is a proportional relationship between a volume measured in cups and the same volume measured in tablespoons. 3 cups is equivalent to 48 tablespoons, as shown in the graph.

No practice problems for this lesson.