Lesson 5: More Estimating Probabilities

Let’s estimate some probabilities.

5.1: Is it Likely?

  1. If the weather forecast calls for a 20% chance of light rain tomorrow, would you say that it is likely to rain tomorrow?
  2. If the probability of a tornado today is $\frac{1}{10}$, would you say that there will likely be a tornado today?
  3. If the probability of snow this week is 0.85, would you say that it is likely to snow this week?

5.2: Making My Head Spin

Work with your group to decide which person will use each spinner. Make sure each person selects a different spinner.

Answer the first set of questions on your own.

Spinner A

GeoGebra Applet hRw74pss

Spinner B

GeoGebra Applet GS4E4rjc

Spinner C

GeoGebra Applet CR6zNyZS

Spinner D

GeoGebra Applet d7wPqs9B

  1. Spin your spinner 10 times and record your outcomes.
  2. Did you get all of the different possible outcomes in your 10 spins?
  3. What fraction of your 10 spins were 3s?

    Work with your group to answer the next set of questions.

  4. Next, share your outcomes with your group and record their outcomes.

    1. Outcomes for spinner A:
    2. Outcomes for spinner B:
    3. Outcomes for spinner C:
    4. Outcomes for spinner D:
  5. Do any of the spinners have the same sample space? If so, do they have the same probabilities for each number to result?
  6. For each spinner, what is the probability that it ends on the number 3? Explain or show your reasoning.
  7. What is the probability that you will spin something other than a 3 on each spinner? Explain or show your reasoning.
  8. When Noah spun spinner D, he put it on his closed binder and never got a 1 in all 10 spins. How might you explain this problem?
  9. When Han spun spinner C, he never got any 3s, so he says that the probability of getting a 3 is 0. How might you explain this problem?

5.3: How Much Green?

Your teacher will give you a bag of blocks that are different colors. Do not look into the bag or take out more than 1 block at a time. Repeat these steps until everyone in your group has had 4 turns.

  • Take one block out of the bag and record whether or not it is green.

  • Put the block back into the bag, and shake the bag to mix up the blocks.

  • Pass the bag to the next person in the group.

  1. What do you think is the probability of taking out a green block from this bag? Explain or show your reasoning.
  2. How could you get a better estimate without opening the bag?

Summary

Suppose a bag contains 5 blocks. If we select a block at random from the bag, then the probability of getting any one of the blocks is $\frac15$.

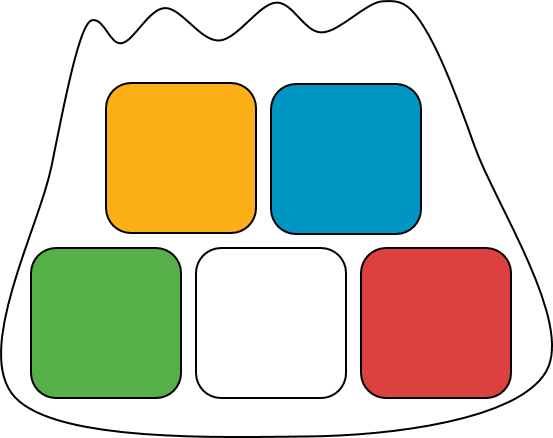
A bag with 5 different colored blocks. The bag contains one yellow block, one blue block, one green block, one white block, and one red block.

Now suppose a bag contains 5 blocks. Some of the blocks have a star, and some have a moon. If we select a block from the bag, then we will either get a star block or a moon block. The probability of getting a star block depends on how many there are in the bag.

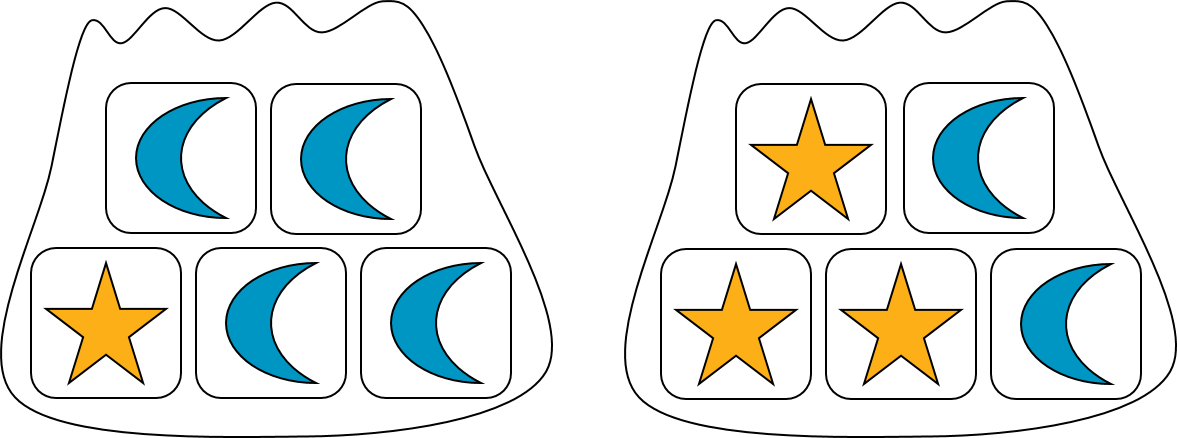
Two bags, each with 5 blocks. The bag on the left contains 4 moon blocks and one star block. The bag on the right contains 2 moon blocks and 3 star blocks.

In this example, the probability of selecting a star block at random from the first bag is $\frac15$, because it contains only 1 star block. (The probability of getting a moon block is $\frac45$.) The probability of selecting a star block at random from the second bag is $\frac35$, because it contains 3 star blocks. (The probability of getting a moon block from this bag is $\frac25$.)

This shows that two experiments can have the same sample space, but different probabilities for each outcome.

Practice Problems ▶