9.1: Still Irrigating the Field
The area of this field is about 500,000 m2. What is the field’s area to the nearest square meter? Assume that the side lengths of the square are exactly 800 m.
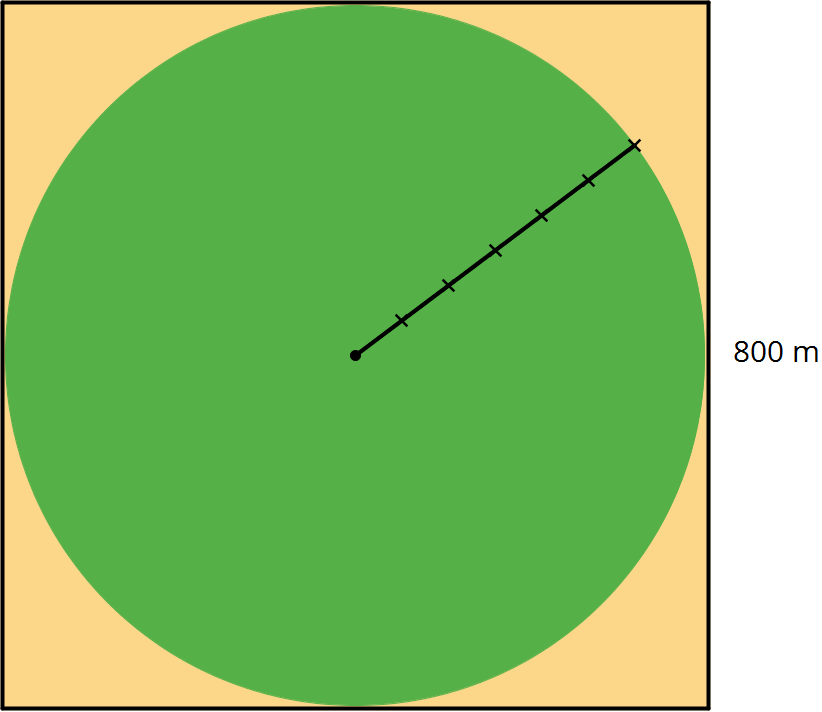
- 502,400 m2
- 502,640 m2
- 502,655 m2
- 502,656 m2
- 502,857 m2
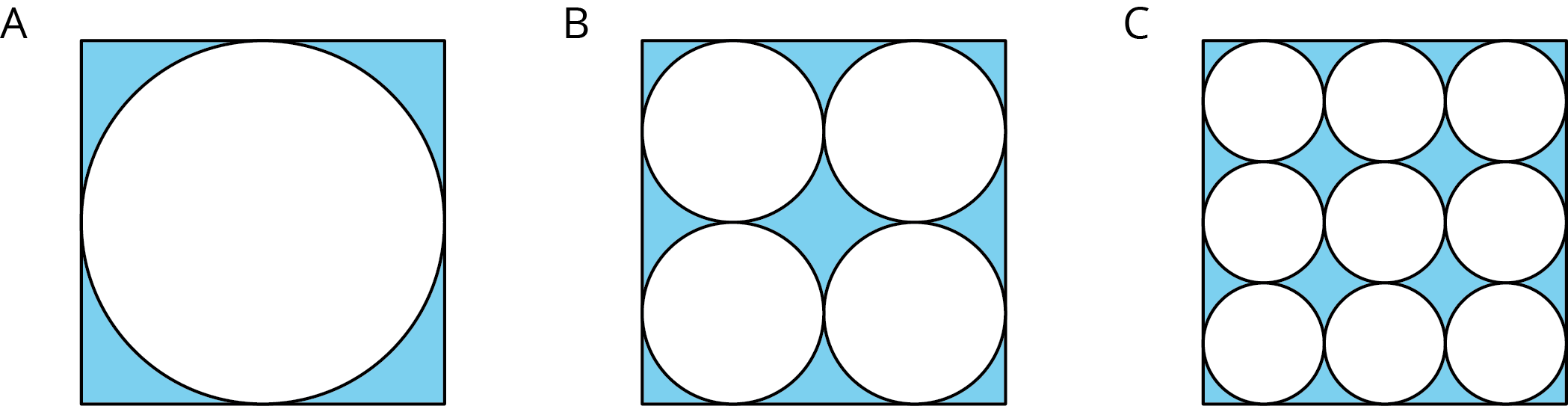
Let’s find the areas of shapes made up of circles.
The area of this field is about 500,000 m2. What is the field’s area to the nearest square meter? Assume that the side lengths of the square are exactly 800 m.

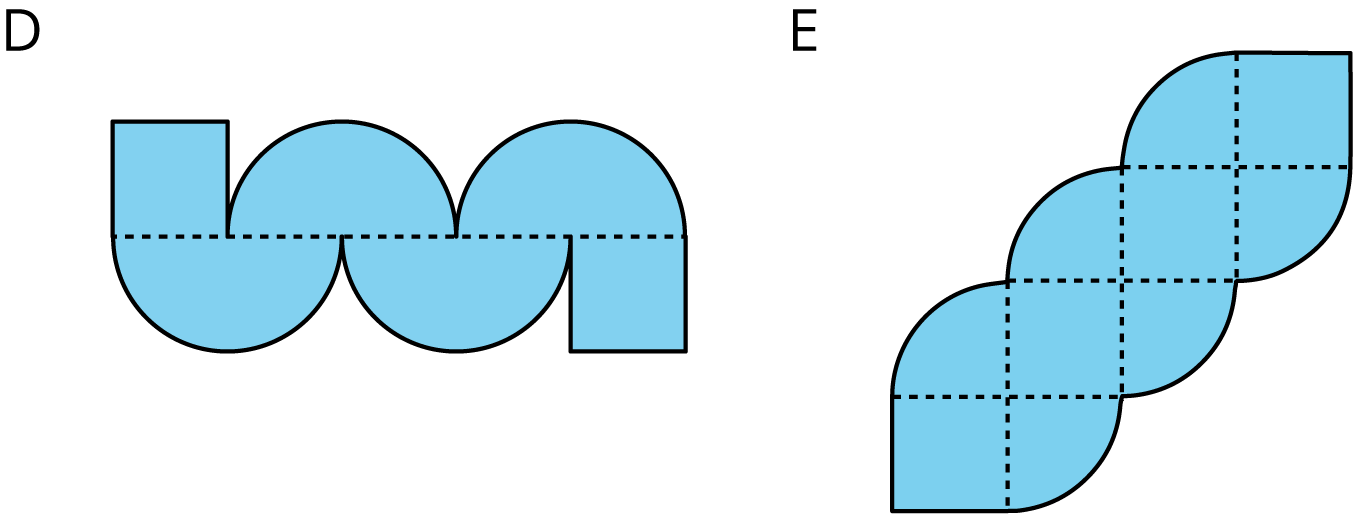
Which figure has a longer perimeter, Figure D or Figure E? How much longer?
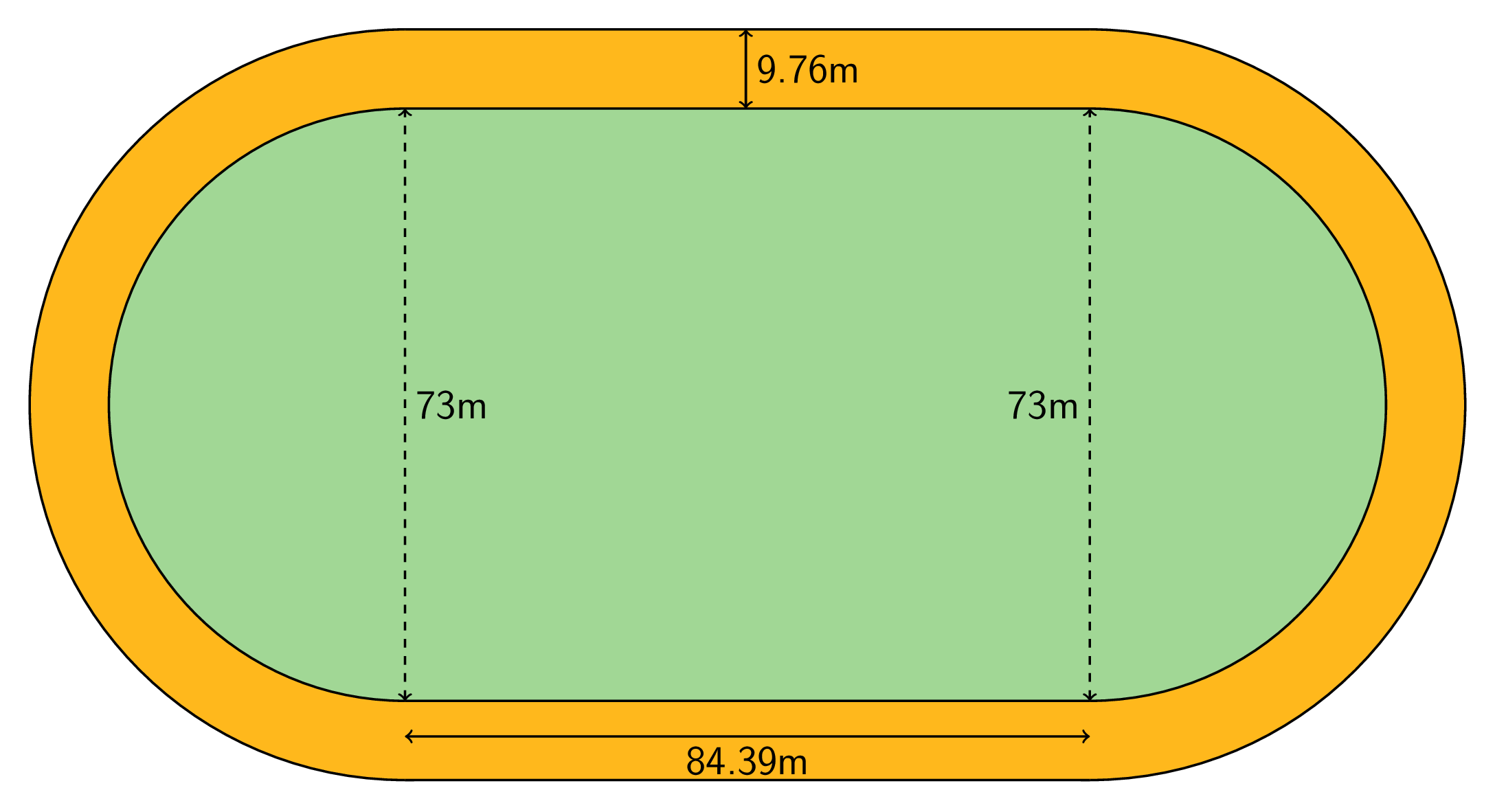
The field inside a running track is made up of a rectangle 84.39 m long and 73 m wide, together with a half-circle at each end. The running lanes are 9.76 m wide all the way around.
The relationship between A, the area of a circle, and r, its radius, is A=\pi r^2. We can use this to find the area of a circle if we know the radius. For example, if a circle has a radius of 10 cm, then the area is \pi \boldcdot 10^2 or 100\pi cm2. We can also use the formula to find the radius of a circle if we know the area. For example, if a circle has an area of 49 \pi m2 then its radius is 7 m and its diameter is 14 m.
Sometimes instead of leaving \pi in expressions for the area, a numerical approximation can be helpful. For the examples above, a circle of radius 10 cm has area about 314 cm2. In a similar way, a circle with area 154 m2 has radius about 7 m.
We can also figure out the area of a fraction of a circle. For example, the figure shows a circle divided into 3 pieces of equal area. The shaded part has an area of \frac13 \pi r^2.
