3.1: Finding Related Statements
Given $a$ and $b$ are numbers, and $a+b=180$, which statements also must be true?
$a=180-b$
$a-180=b$
$360=2a+2b$
$a=90$ and $b=90$
Let’s look at angles that are not right next to one another.
Given $a$ and $b$ are numbers, and $a+b=180$, which statements also must be true?
$a=180-b$
$a-180=b$
$360=2a+2b$
$a=90$ and $b=90$
Use any useful tools in the geometry toolkit to identify any pairs of angles in these figures that are complementary or supplementary.

Use a straightedge to draw two intersecting lines. Use a protractor to measure all four angles whose vertex is located at the intersection.
Find the measure of the angles in one column. Your partner will work on the other column. Check in with your partner after you finish each row. Your answers in each row should be the same. If your answers aren’t the same, work together to find the error and correct it.
| column A | column B | |
|---|---|---|
| row 1 |
$P$ is on line $m$. Find the value of $a$.
|
Find the value of $b$. 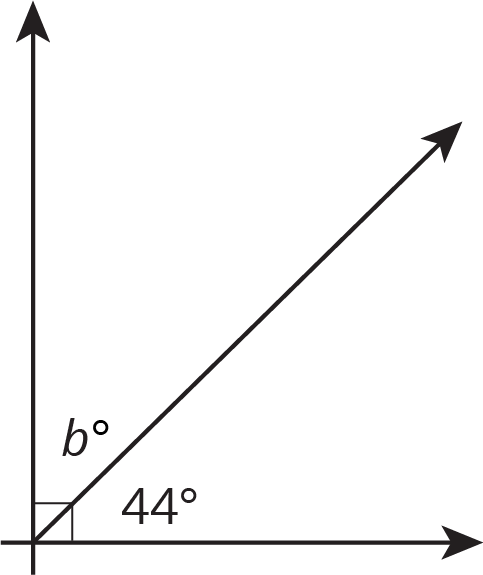
|
| row 2 |
Find the value of $a$. 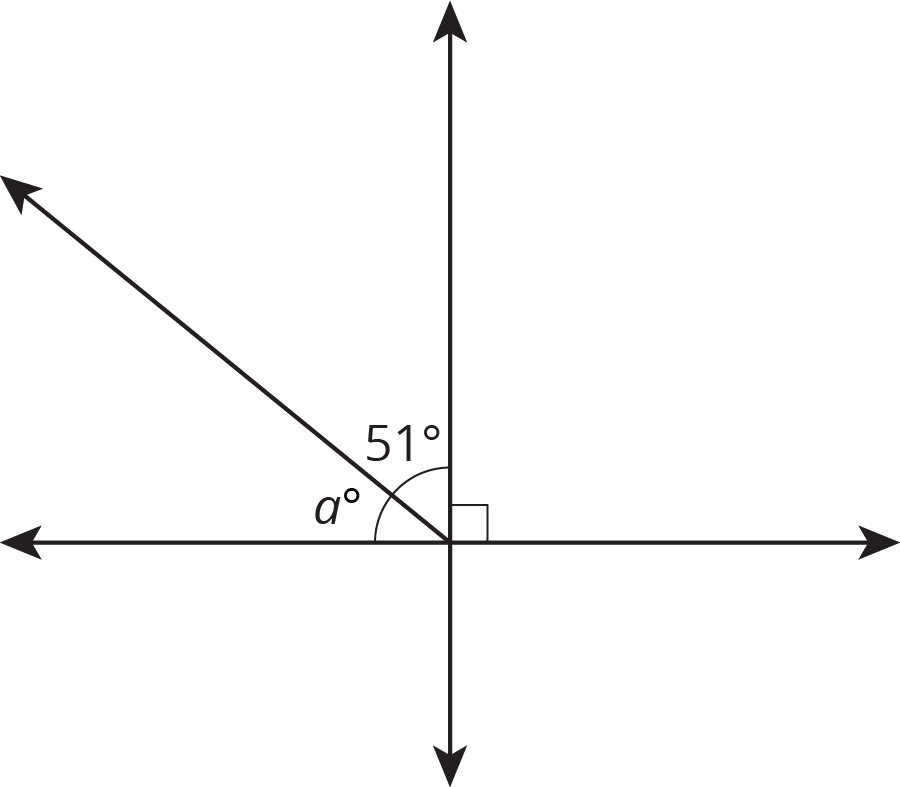
|
In right triangle $LMN$, angles $L$ and $M$ are complementary. Find the measure of angle $L$.
|
| column A | column B | |
|---|---|---|
| row 3 |
Angle $C$ and angle $E$ are supplementary. Find the measure of angle $E$. 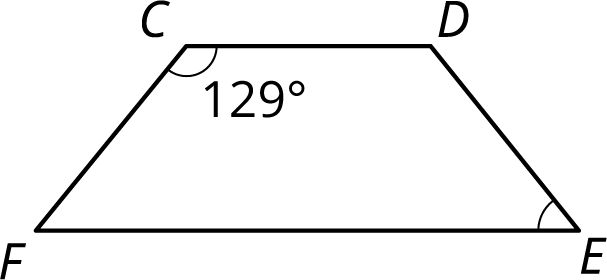
|
$X$ is on line $WY$. Find the value of $b$. 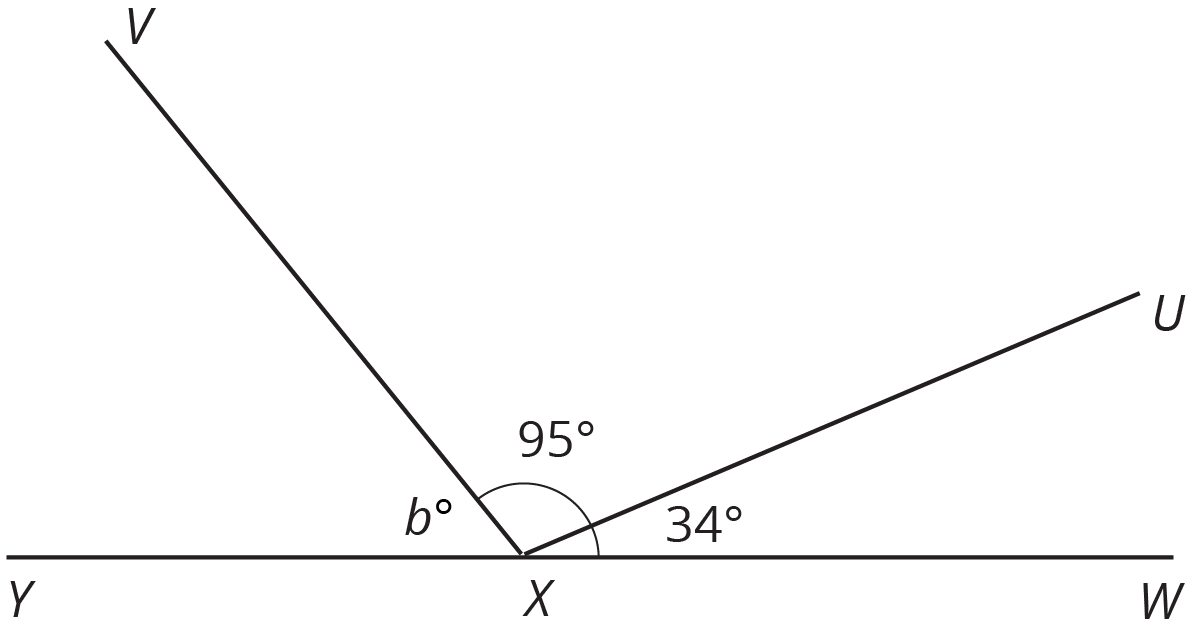
|
| row 4 |
Find the value of $c$. 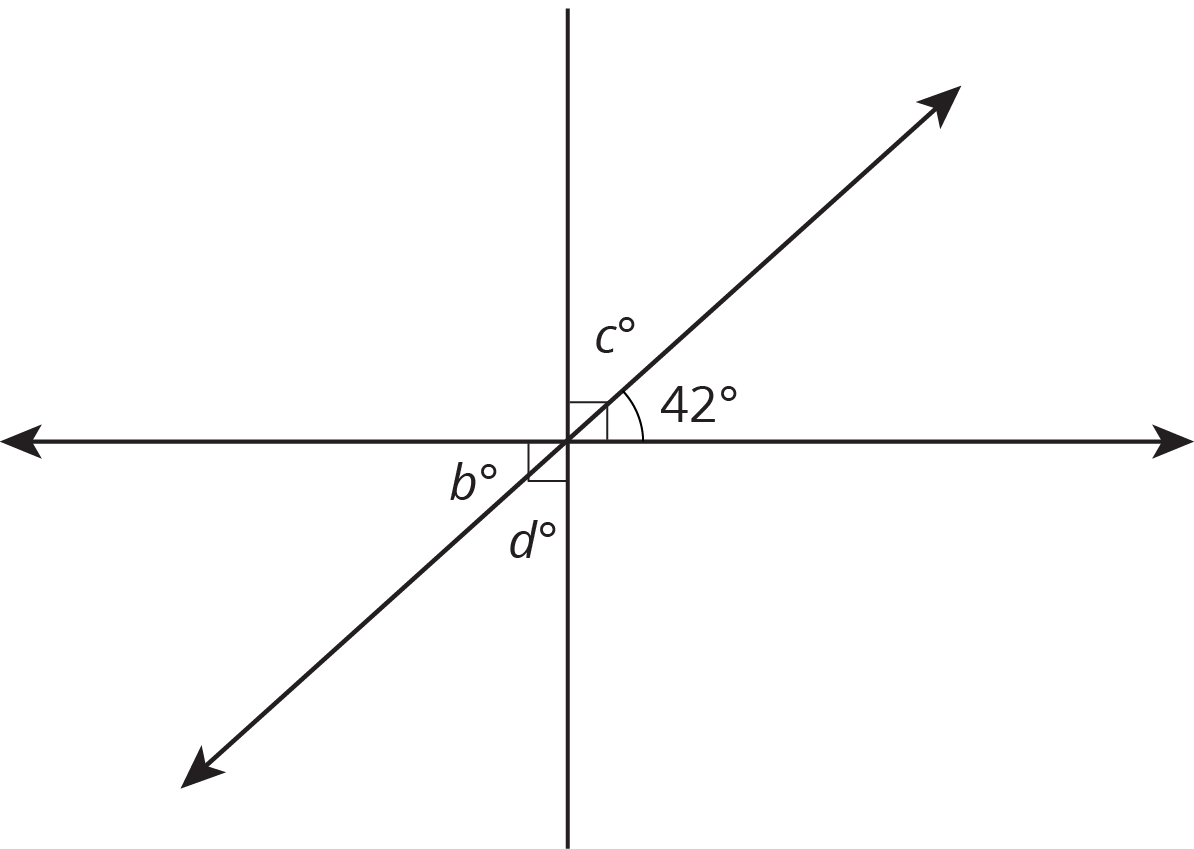
|
$B$ is on line $FW$. Find the measure of angle $CBW$. 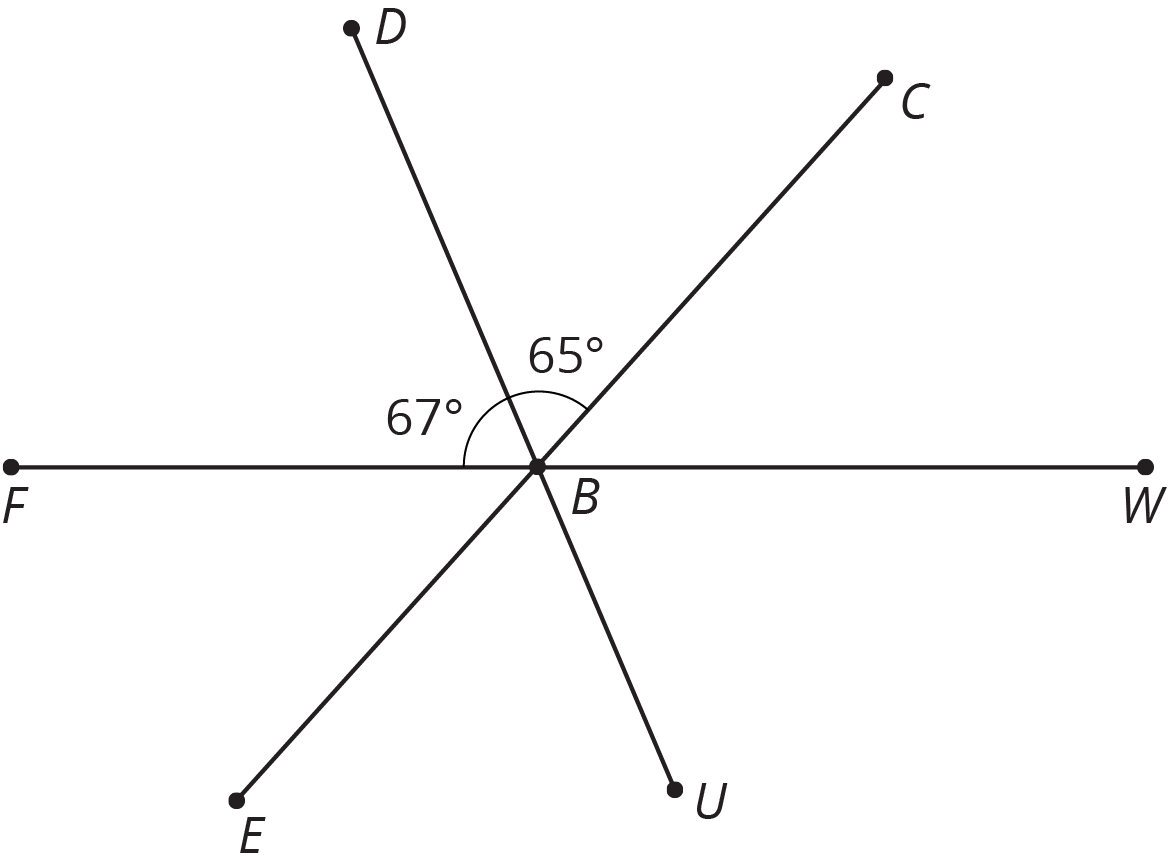
|
| row 5 |
Two angles are complementary. One angle measures 37 degrees. Find the measure of the other angle. |
Two angles are supplementary. One angle measures 127 degrees. Find the measure of the other angle. |
When two lines cross, they form two pairs of vertical angles. Vertical angles are across the intersection point from each other.
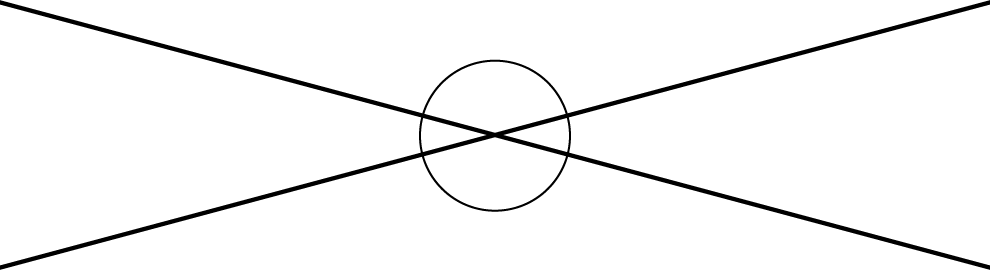
Vertical angles always have equal measure. We can see this because they are always supplementary with the same angle. For example:

This is always true!

$a+b = 180$ so $a = 180-b$.
$c+b = 180$ so $c = 180-b$.
That means $a = c$.
A pair of vertical angles is a pair of angles that are across from each other at the point where two lines intersect. There are two pairs of vertical angles.
